自适应遗传算法在飞行器离线航迹规划中的应用

郝 震，张 健，蔡满意

(空军工程大学工程学院，西安 710038)

0 引言

在飞行器低空突防的TF/TA2过程中，要根据任务区域的地形、地物和威胁以及飞行器性能等约束进行飞行航迹规划，得到最优飞行航迹，提高飞机生存率和完成任务的概率［1］。

在范围较大的任务区域，用动态规划进行航迹规划，信息处理量太大。由于地形曲面复杂，基于梯度法优化算法很难得到全局最优航迹。A*算法计算简单容易实现，但启发函数的选取限制了解的全局最优性。针对低空突防的特殊要求，将基本遗传算法改进，提出一种自适应遗传算法，使飞行航迹严格经过飞机的起始点和目标点，使威胁飞机的因素最小，有效地提高了飞机的任务生存概率。

1 航迹规划各种约束分析

为了让规划出的航迹更符合实际，对各种约束条件进行分析，使航迹满足这些约束条件。按航迹规划约束来源的不同，将约束划分为以下4类:

1)任务战术约束，任务完成时间t，起始点S(xS，yS，zS)，目标点 T(xT，yT，zT)，攻击方位角 ψ0，初始航向ψ0;

2)威胁约束，雷达发现概率Pdetection，飞行器撞地概率Pcollision，最小横侧向离地间隙Δdmin，最小离地高度Δhmin;

3)飞行器性能约束［2］，最小平飞速度Vmin，最大平飞速度Vmax，航程Lmax，最大飞行高度Hmax，水平最小转弯半径 Rmin，最大爬升角 θmax，最大航迹偏角 Δψmax，最大纵向曲率ρmax，最大过载nzmax;

4)其他约束，最小航迹步长lmin，最大航迹节点数Nmax。

2 规划空间建模、地形预处理以及威胁建模

在规划空间建模问题中，为研究方便且不失一般性，航迹规划算法仿真验证时，模拟生成一块数字地形，以代替真实数字地图，作为算法验证的环境。其中用指数函数模拟算法模拟山峰地形，用正余弦函数模拟算法模拟山脉地形，用随机模拟算法模拟随机地形，最后生成综合模拟地形［3］;对于生成的数字地形预处理，利用二维三次卷积插值算法对数字地形插值平滑［4］;在威胁建模方面，考虑了低空突防中可能遭遇的地形威胁和雷达探测威胁，并把孤立山峰当作威胁来处理［5］。

将飞机的最小离地高度、最小横侧向离地间隙、坡度限制、最大纵向曲率和威胁这些约束条件融入到数字地形预处理中，生成了安全飞行曲面［6］，在安全曲面上进行二维航迹规划，缩减了规划的维数，降低了问题的复杂度。

3 自适应遗传算法

3.1 基本遗传算法

基本遗传算法已经得到了广泛的应用，但有两个严重的缺点:容易早熟收敛和进化后期搜索效率较低。基本遗传算子采用适应度比例选择、单点交叉和单点变异方法进行遗传操作。由于选择及交叉算子的作用，使得一些优秀的基因片段过早丢失，限制了搜索范围，造成了算法的早熟收敛。

3.2 遗传算子的改进

为了克服这些缺点，对基本遗传操作进行改进，提出了新的选择、交叉和变异算子。

1)排序选择算子和最优解保存算子。

排序选择算子是首先根据个体的适应度大小进行排序，然后基于排序号进行选择。最优解保存算子的思想是把群体中适应度值最优的解不进行配对交叉，而直接复制到下一代中。其优点是:进化过程中某一代的最优解可以不被交叉和变异操作所破坏，并总能收敛至最(次)优解。

2)多点交叉算子。

采用两点交叉和单点交叉相结合的方式。通过增加交叉方式，增强算法的全局搜索能力，防止陷入局部最优。两点交叉设置两个交叉点，将两个交叉点之间的同组基因进行基因的互换。因而当染色体长为n时，则可能有(n－2)(n－3)种交叉点的设置。

3)高斯变异算子［7］。

采用高斯算子变异方式，让变异与适应度紧密相联，防止变异对适应度较优的个体的损伤，按变异率选择某个体(这里选定k染色体)按下式变异:

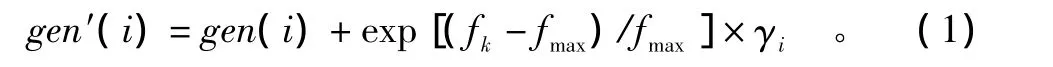
式中:gen′(i)，gen(i)分别为新生代和父代个体的第i个基因;fmax、fk分别为本代个体的最优适应度和第k个个体的适应度。γi为均值为0、方差为1的高斯随机变量。当gen(i)超出基因位数值范围时，则重新产生γi变异，直到满足要求为止。

3.3 自适应遗传算法

在基本遗传算法的运行过程中，选取固定的交叉概率和变异概率控制参数易产生早熟现象，陷入局部极值，但是选择较大的交叉和变异概率就会成为随机搜索，选择较小的交叉和变异概率又不容易跳出局部极值点。可以通过协调交叉概率Pc和变异概率Pm达到使算法收敛于全局最优和抑制早熟。各染色体差异越小，则给定的交叉和变异概率愈大，这样在群体中的各个体过分趋于一致时，会使交叉和变异的可能性增加，从而提高群体的多样性，增强算法的搜索能力;而在群体多样性已经很强时，则减少交叉和变异概率，以免破坏优良个体。但是增大交叉概率Pc和变异概率Pm的值，将增大算法的运行时间。使用中等大小的交叉概率Pc(0.5～1.0)和小的变异概率 Pm(0.01～0.15)，根据适应度值的大小，自适应改变交叉和变异概率的大小来达到全局优化和运算时间折中的目的。

通过观察种群的平均适应度favg和种群最优适应度fmax的关系来判别算法是否收敛于最优。Pc和Pm值的大小依赖于favg－fmax的变化。当整个种群趋于收敛时，即favg－fmax变小时，增大Pc和Pm;反之，减小Pc和Pm。因此构造Pc和Pm表达式为

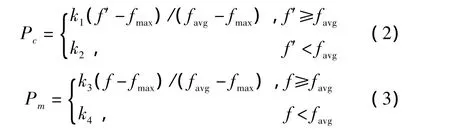
式中:f′代表要交叉的两个个体中较大的适应度值;f代表要变异的个体的适应度值;0≤k1≤1;0≤k2≤1;0≤k3≤1;0≤k4≤1。

自适应遗传算法通过式(2)、式(3)实现根据染色体适应度大小来自适应调整其交叉概率和突变概率［8］，当算法陷于局部最优时，favg－ fmax将减小，由表达式可知，Pc和Pm增大，增大了搜索范围;当解空间过于分散时，favg－fmax增大，而Pc和Pm值减小，从而缩小搜索范围。对于 k2和 k4，由于此时 f′≥favg或 f≥favg，即个体适应度大于平均适应度，说明个体特性差，增大Pc和Pm，使差的个体破坏的可能性增大，k2和k4的值就大一些。

4 自适应遗传算法仿真

4.1 航迹极坐标编码方式

航迹极坐标编码方式［9－10］是利用航迹点极坐标序列来表示航迹。如图1所示，S、T分别为起始点和目标点。(1，2，…，N －1)分别为航迹点序号，与 S、T 构成N个航迹段，航迹点(1，2，…，N－1)的极径依次为1ρ0，2ρ0，3ρ0，…，(N －1)ρ0。其中，ρ0为航迹点 1 所在圆弧的半径，且 ρ0=ρT/N。

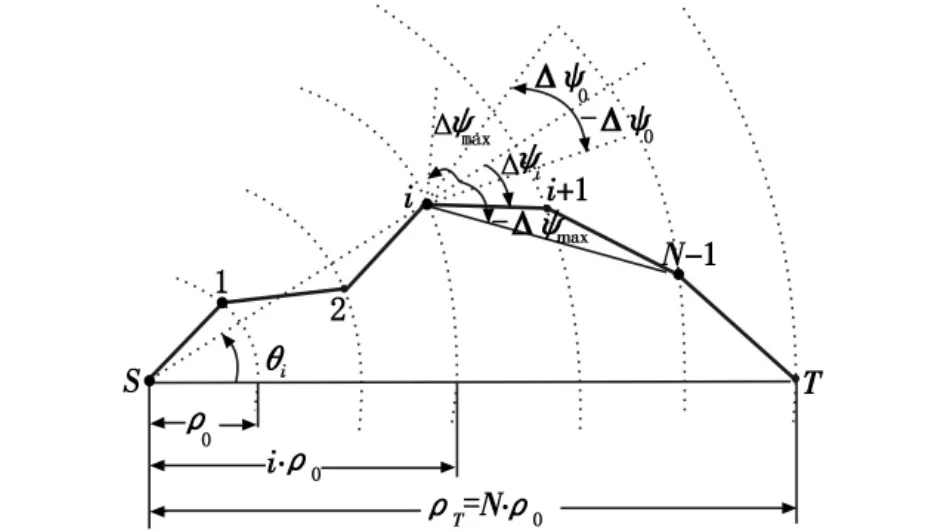
图1 航迹偏角的极坐标编码方式Fig.1 Flight path polar coordinate coding mode

通过以上处理，只需对航迹点的极角编码即可，若航迹点编码为(θ1，θ2，…，θN－1)。结合起始点和目标点的极坐标，则该条航迹的极坐标序列为

由于只需对极角进行编码，大大减少了航迹规划的时间，提高了效率。

利用直角坐标和极坐标的关系，将式(4)的航迹点极坐标序列解码转换到规划空间的直角坐标系中，就得到了直角坐标系下的航迹点坐标。

采用航迹偏角调整尺度Δψ0的倍数作为染色体编码的基因位。若航迹染色体的第i个基因值为gi，则第 i个航迹段［i－1，i］偏离第 i－1个航迹段［i－2，i－1］的航迹偏角 Δψi=gi·Δψ0，其中Δψ0、Δψi、Δψmax的含义如图 3 所示。若 Δψmax/Δψ0=M，则航迹染色体各基因位的取值范围为 gi∈[－M，…，－2，－1，0，1，2，…，M ]，基于这种航迹偏角的极坐标编码方式，解决了最大航迹偏角、最小航迹步长、最大航迹点数3个约束。

4.2 航迹适应度函数

若一条航迹由染色体X表示，代价函数为

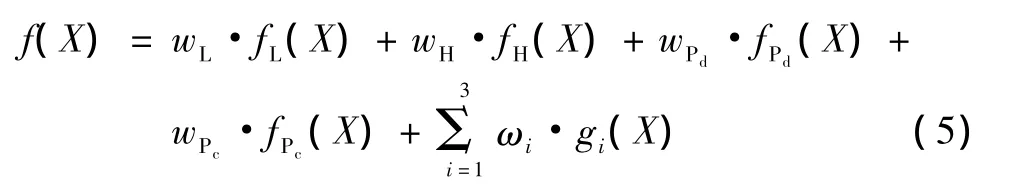
其中:优化项 fL(X)、fH(X)、fPd(X)、fPc(X)分别表示航迹长度代价、航迹高度代价、雷达发现概率代价和飞行器撞地概率代价;wL、wH、wPd、wPc为对应的各航迹子代价在航迹总代价中所占的权重，且满足wL+wH+wPd+wPc=1。用层次分析法［11］对权重进行分配，这里令wL=0.0582，wH=0.1052，wPd=0.2603，wPc=0.5762。

代价函数惩罚项:

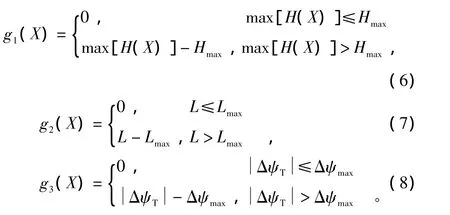
这里令:ω1=1000，ω2=10000，ω3=100000，使那些违背无人机性能约束的航迹个体的代价值非常大，从而在进化过程中被淘汰。

航迹适应度函数:

其中:f(X)为航路染色体X的代价。进而问题由代价最小化转化为航迹适应度最大化。

4.3 遗传操作算子

1)选择算子。将当代适应度最大的10个染色体复制两份，一份不经过交叉和变异直接复制到下一代中，另一份取代由于适应度最小而被淘汰的10个染色体，将中间的染色体复制一份产生下一代，直到被进化产生的更优个体所取代为止。

2)交叉算子。采用两点交叉和单点交叉相结合的交叉算子。

3)变异算子。在航迹染色体的世代进化时，采取在［－M，M］内进行实值高斯变异。

4)对于算法参数，结合仿真，对自适应交叉概率和变异概率进行改进:

4.4 仿真参数

遗传算法的参数:初始种群数目100;进化代数300;自适应交叉概率Pc1=0.9，Pc2=0.6;自适应变异概率 Pm1=0.01，Pm2=0.001。

雷达参数有R1位置(25，50)，作用半径12;R2位置(45，25)，作用半径 12;R3位置(60，55)，作用半径15;R4位置(75，75)，作用半径 10。

任务参数:起始点S(10，10);目标点T(90，90)。

进入方位角+45°(目标左侧进入)，裕度5°。

4.5 仿真结果验证

在Matlab 7.0集成环境下仿真结果见图2～图4。

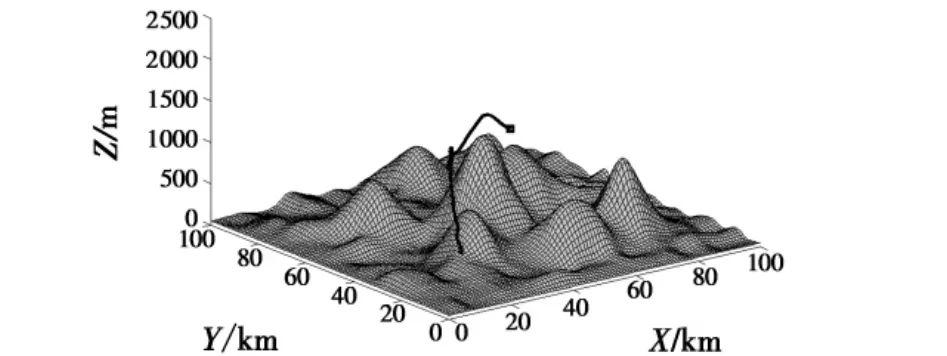
图2 三维航迹曲线Fig.2 Three-dimensional flight path curve

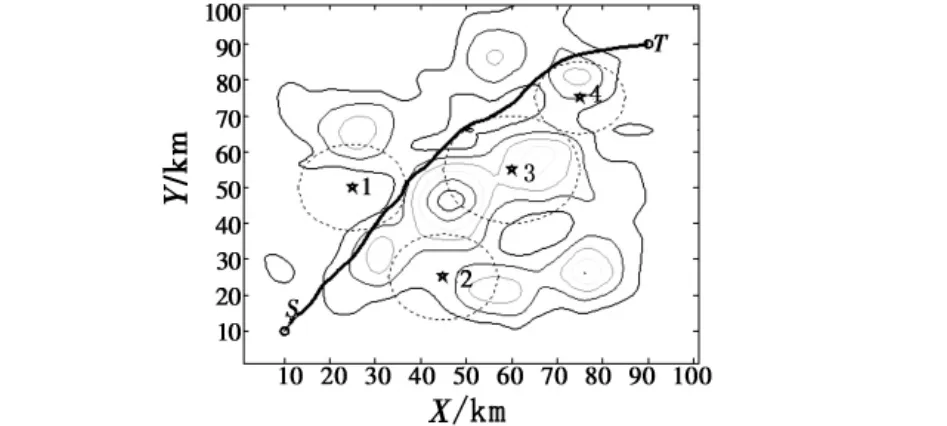
图3 水平航迹曲线Fig.3 Horizontal flight path curve

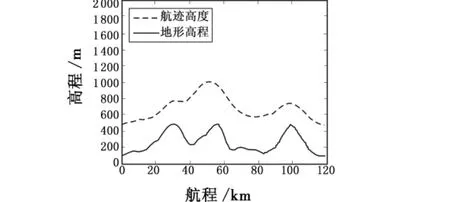
图4 纵向航迹曲线Fig.4 Longitudinal flight path curve

在图2中，曲线表示生成的飞行器三维航迹。在图3中，五角星表示突防区域内的威胁，以五角星为圆心的点线圆圈表示了各雷达的最大作用范围，由于对探测威胁是用雷达发现概率Pdetection来处理，R1半径越大，则Pdetection越小，并考虑到该区域周围的飞行器撞地概率，因而航迹穿过于R1作用范围的边缘是可以接受的，也符合实际情况。在图4中，实线表示地形高程，虚线表示各航迹点的高度。由仿真结果可以看出，飞行器较好地实现了TF/TA2。

5 结束语

针对飞行器航迹规划多约束三维规划问题，生成安全飞行曲面和采用极坐标编码方式，将复杂的三维规划问题转化为一维问题，部分约束融入到安全飞行曲面和极坐标编码方式中，减少了规划时间。为避免局部最优，采用自适应交叉和变异概率，提高了遗传算法的全局寻优能力，使规划出的最(次)优航迹更加稳定，得到了较满意的实际效果。

［1］闵昌万，袁建平.军用飞行器航迹规划综述［J］.飞行力学，1998，16(4):14-18.

［2］吴强，曹义华，金长江.最小安全飞行高度的计算［J］.战术导弹技术，2003(2):21-24.

［3］李栋，曹义华，冯婷.基于地形特征的简易地形模拟算法［J］.航空计算技术，2005，35(2):32-35.

［4］孙向春.直升机飞行航迹规划与控制跟踪技术研究［D］.北京:北京航空航天大学，2004.

［5］胡志忠，徐克虎，沈春林.低空突防用数字地图信息的融合处理［J］.南京航空航天大学学报，2000，32(4):434-438.

［6］唐强，王建元，朱志强.基于粒子群优化的三维突防航迹规划仿真研究［J］.系统仿真学报，2004，16(9):2033-2036.

［7］范洪达，马向玲，叶文.飞机低空突防航路规划技术［M］.北京:国防工业出版社，2007.

［8］王小平，曹立明.遗传算法理论应用与软件实现［M］.西安:西安交通大学出版社，2002.

［9］李娜，张海.基于遗传算法的军用飞行器航迹规划［J］.战术导弹控制技术，2004(3):86-94.

［10］马云红，周德云.基于遗传算法的无人机航路规划［J］.电光与控制，2005，12(5):24-27.

［11］张红，卢广山，朱荣刚.无人作战飞机任务系统技术研究［J］.电光与控制，2006，13(1):55-59.