基于矩阵分析的DS理论在组网雷达中的应用

曲大鹏，张 斌，黄 俊

(空军工程大学工程学院，西安 710038)

0 引言

单站雷达由于受其自身性能、精度、探测角度、位置、外部环境等因素的影响，在进攻方远距离支援干扰飞机和随队掩护支援干扰飞机的压制和欺骗干扰下，无法对来袭目标做较为理想的识别判定。而组网雷达由于其空间的分置、多种雷达体制的组合以及多信息的融合，给其目标识别带来了较大的优势［1］。

在各种融合算法中，DS证据理论因其在区分不知道与不确定方面以及精确反映证据收集方面显示出的灵活性更加适合于目标识别领域的应用。但如何获得合理的基本概率赋值是使用证据理论的一个重要问题。同时，由于计算融合结果所需的时间会随着焦元个数的增加急剧增长，巨大的计算量也阻碍了DS证据理论得到更广泛应用［2－10］。

文献［1－2］分别给出利用模糊隶属度求基本概率的方法，但计算过于复杂，不利于编程实现。对于证据理论焦元爆炸问题，Denceux提出了证据推理的神经网络实现;Mamer提出的先验条件一致度具备距离的性质，可以作为删除焦元前后证据变化的量度，而用证据对焦元灵敏度的方法删除不必要证据［3］。本文针对以上问题提出在模糊信息下确定基本概率赋值函数的方法并利用目标识别的置信度分配矩阵这一特殊的证据组合结构，提出了一种应用于组网雷达目标识别的快速融合算法。

1 证据理论方法

证据合成法则是为了同时利用来自相互独立的不同信息源证据，提高对事件的置信程度而提出的一种多信息体的组合法则。

设Bel1，Bel2，…，Beln是同一辨识框架Θ上的信度函数，m1，m2，…，mn分别是其对应的基本可信度分配。如果Bel1⊕…⊕Beln存在且基本可信度分配为m，则n个信度函数的组合为(((Bel1ε Bel2)ε Bel3)ε…)ε Beln，式中ε表示正交和，由组合证据获得的最终证据与其次序无关。

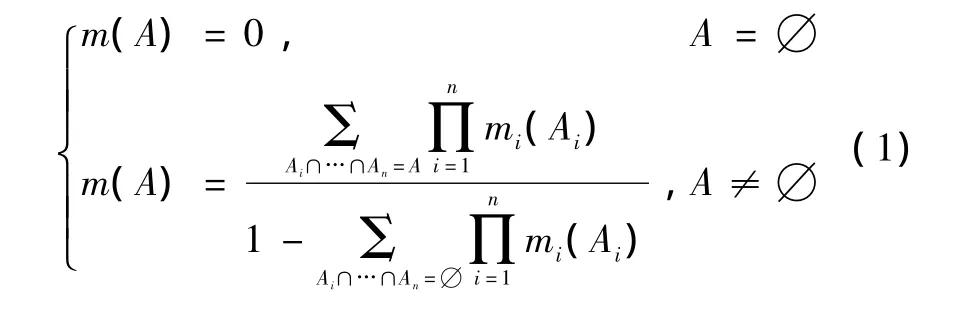
2 模糊信息下基本概率赋值函数的确定

首先基于随机集理论刻画模糊信息的隶属函数，获得模糊观测下具有概然特性的隶属函数，该似然函数表示在收集的模糊信息下确定为某一目标的可能性，在数值上表示传感器信息对某一命题支持的程度，利用似然函数确定传感器输出的基本概率赋值。

假设有一个目标数据库，它包含了各种目标的特征参数，将这一数据库设为论域U，目标为t时的特征参数以及传感器m对该目标特征参数的测量是该论域的模糊子集。则目标和传感器观测的特征属性分别用模糊隶属函数 μt∶U→［0，1］和 μm∶U→［0，1］表示。设A为一个在区间［0，1］上均匀分布的随机数，并定义:

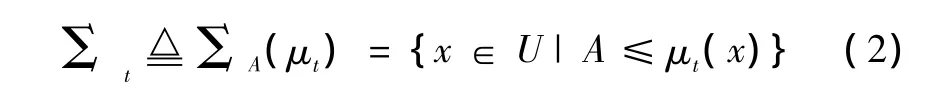
式中:Σt表示目标特征属性空间中隶属函数大于A的元素的集合，在模糊数学中称为截集。截集是一个集合，且该集合是随机的，它是一种随机集。同理，传感器观测的数据也有截集Σm。如果Σt与Σm有交集，则可以认为它们匹配，也就是说传感器观测到的是目标t。直观上说，如果它们经常性地匹配，则可以认为传感器观测确实是由目标t引起的;如果匹配的次数很少，则可以认为不是由t引起的。因此，可以给出一个似然测度:

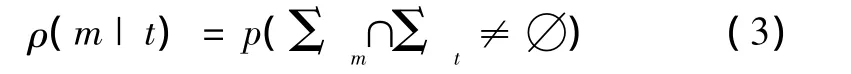
它是由观测m与产生该观测目标t的匹配概率，其数值上的大小反映了在目标为t时，观测应该为m的似然程度。

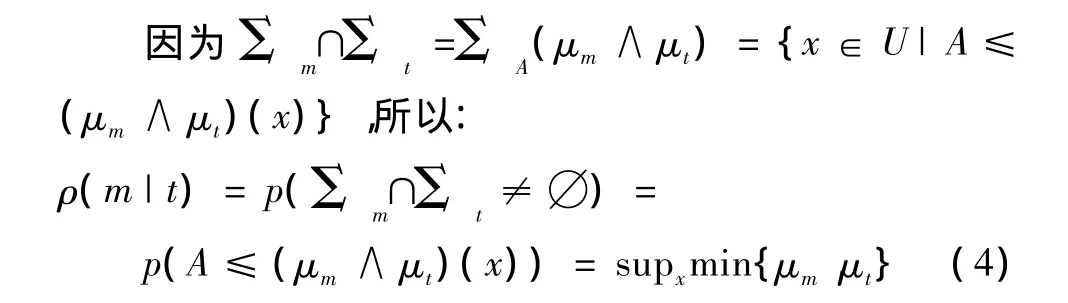
式(4)是对每一个变量x的μm(x)和μt(x)进行取小运算所得到的比较小的数里面取最大的数。利用高斯属性的模糊隶属函数举例说明。在特征属性为发射频率f时，目标和传感器观测的隶属函数分别为

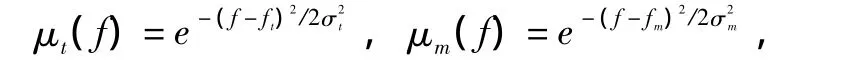
设有两种目标类别a，b和一个传感器，模型库中a，b的发射频率和传感器观测到的发射频率分别为fa=12 MHz，σa=3，fb=24 MHz，σb=3，fm=20 MHz，σm=3，则μa(f)，μb(f)和 μm(f)如图1 所示。

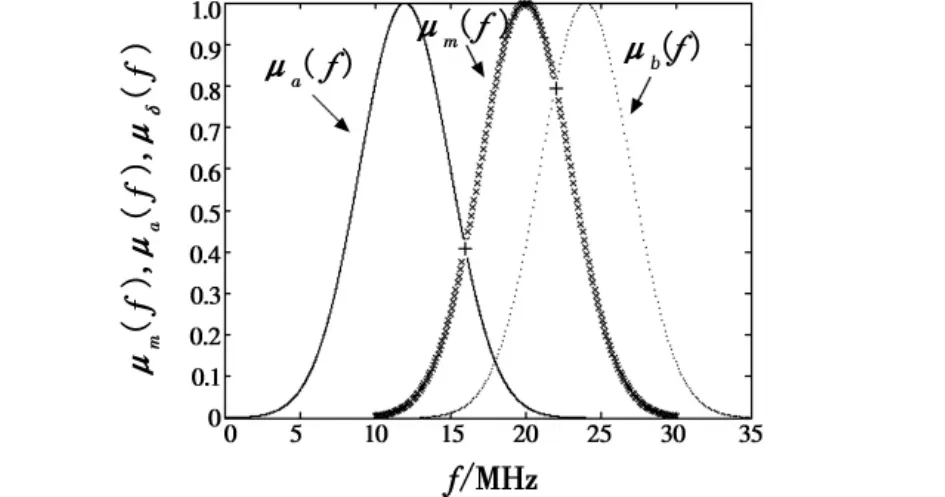
图1 传感器观测的结果Fig.1 The result of sensor’s observation

在图1中，μa(f)和μb(f)分别与μm(f)相交部分纵坐标的最大点(在图中为“+”所示)就是两种目标的似然测度值:ρ(m|b)=0.8007，ρ(m|a)=0.4111。

它们的值越大，则传感器观测与该类别目标越匹配。从证据理论的角度看，传感器收集的这一数值表明了对某一命题的支持程度，但还不能将其作为证据理论中的基本概率赋值。因为证据理论中，基本概率赋值必须满足归一化条件。因此，当模型库中有多种目标时，可以利用上述似然函数确定求出该传感器观测信息对各个目标的支持程度。然后将这些支持程度进行归一化处理求出证据理论所需的基本概率赋值。

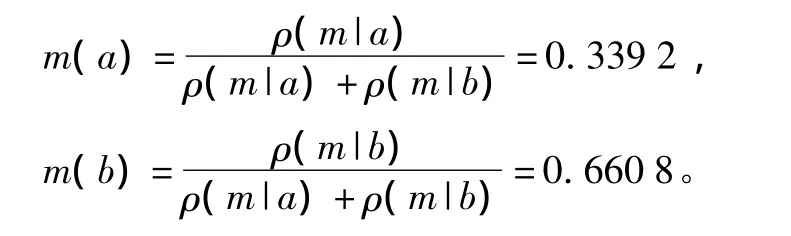
3 基于矩阵分析的融合算法

3.1 算法描述

在传感器网络中假设有p个传感器，被识别的目标总共有q种可能。则由p种传感器确定的基本概率赋值可表示为

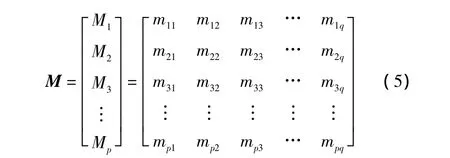
其中M中任一元素mpq表示第p个传感器识别目标为第q种类型的基本概率赋值。用矩阵中的一行的转置与另一行相乘。得到一个q×q的新矩阵A:

主对角线上的元素之和就是2个信度函数组合结果中的分子，而非主对角线上的元素之和构成了证据的不确定因子K12。即:

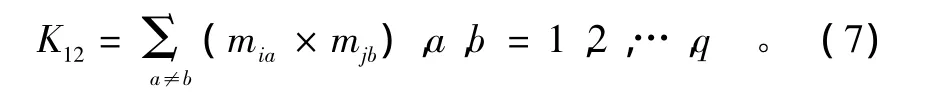
假设Φ是矩阵中主对角线元素之外其余元素的和，即

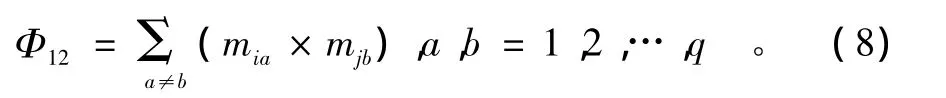
在融合第3个传感器的数据时，将A的主对角线上的元素构成q×1的矩阵Z与1×q的矩阵Mt相乘得到新的矩阵A:

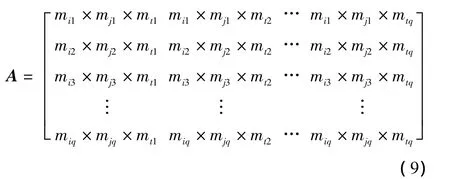
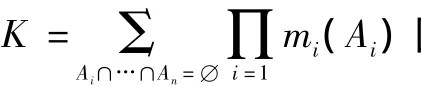
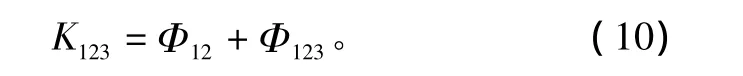
依次类推，在经过了p－1次融合后得到矩阵A如(11)式所示。

由矩阵A就可以得到p个传感器目标识别的基本概率赋值的累积以及证据的不确定因子K。

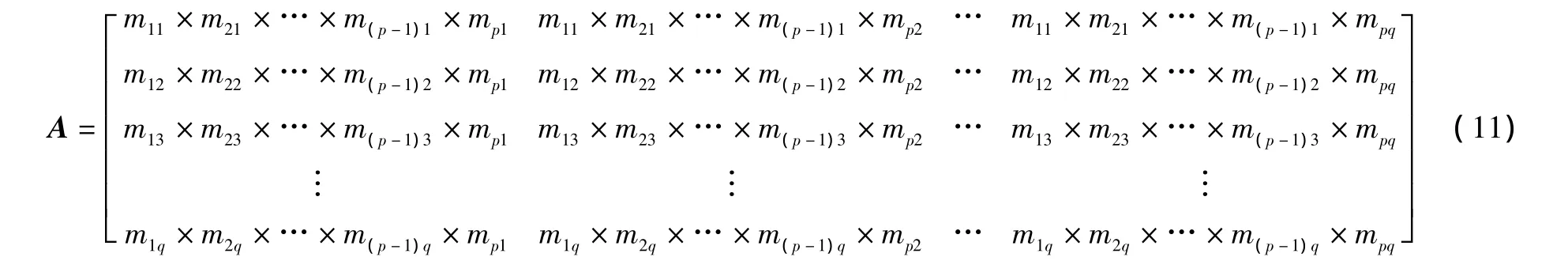
3.2 算法分析

对于DS多个信度函数的组合式(1)，由于要进行p元乘法运算，且每个因子可能的取值有q个，所以计算该式所需的时间为t(qp)。本文应用的算法，在每一次执行过程中都完成了一个q维列向量与一个q维行向量的矩阵乘法运算，计算需要的时间应为t(q2)。而要得到融合结果需要执行p－1次算法，因此，整个计算过程的时间为t((p－1)q2)。因此，随着传感器的增加DS原始算法的计算量会呈指数增加，而本文的算法只会呈线性比例关系。

4 算法的应用及仿真

设分布式组网雷达中部署了4部传感器，它们协同工作，共同完成对空中来袭目标的探测和告警。识别框架Θ定为歼击机、轻型轰炸机、中型轰炸机、重型轰炸机以及其他飞行器5种目标类别。通过前文所给出的模糊函数求解出由这4部传感器确定的某一目标的基本概率赋值如表1所示。用矩阵分析得出的结果如表2所示。

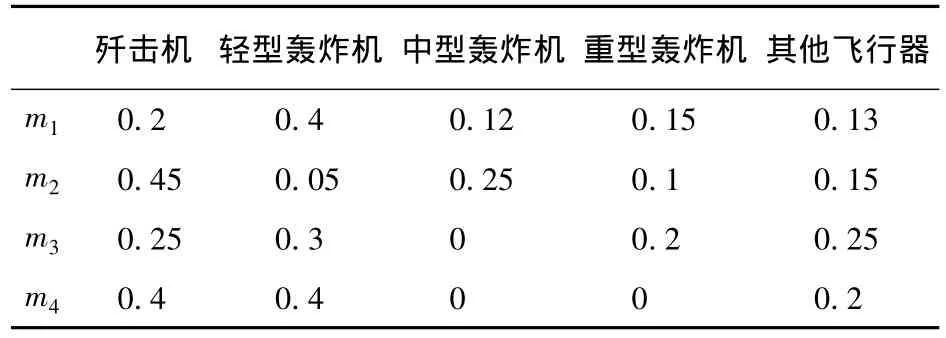
表1 4部传感器确定的基本概率赋值Table 1 Basic probability decided by 4 sensors

表2 基于矩阵分析的DS理论的结论Table 2 Result of evidence theory based on matrix analysis

同样假设对于给定的目标有5种目标类型。则根据前文的结果可得使用DS证据理论所需要的时间为t(5p)，使用矩阵分析的方法所需要的时间为t(25(p－1))，这里p为对该目标进行识别的传感器的数目。对证据理论和基于矩阵分析的传感器数目与运行时间的关系分别进行仿真，仿真结果如图2、图3所示。

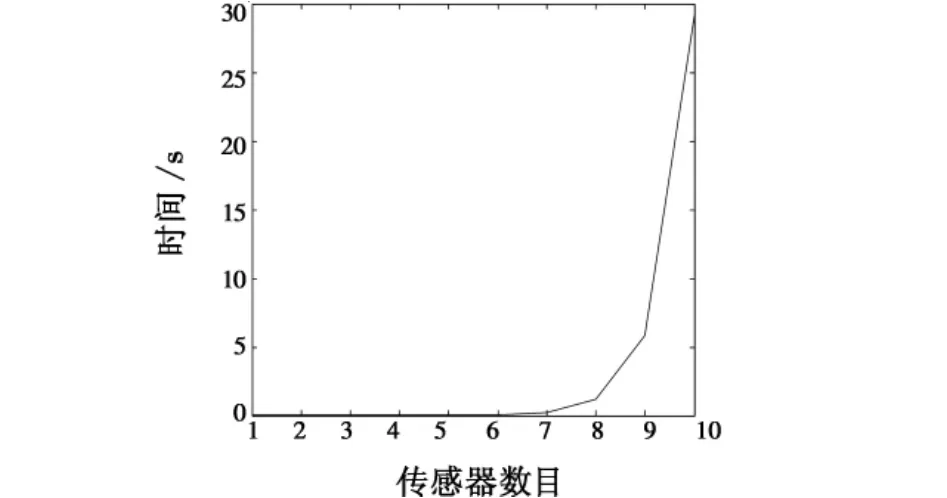
图2 证据理论运行时间Fig.2 Processing time of evidence theory

由图3和图4的比较可以发现，证据理论与基于矩阵分析的证据理论比较，在传感器数目偏少时运行的时间相差不大，但是当传感器数目多于8个时，运行时间呈指数上升，也就是出现了指数爆炸。而本文算法的运行时间一直随着传感器数目的增长呈线性增长，在计算时间上有较大的优势。

5 结论

DS证据理论是一种重要的不确定性推理方法，既能处理随机性导致的不确定性，又能处理模糊性所导致的不确定性。模糊信息可以转化为证据理论框架下的基本概率赋值，基于DS组合规则实现模糊性和随机性信息融合。但DS理论在实现时存在的指数爆炸问题成为应用的一大障碍。特别在组网雷达的目标识别等对实时性和同步性要求较大的领域难以有更大的应用。为了避免在推理链较长时，焦元以指数级数递增，造成计算量变大，引起焦元爆炸的问题，本文在矩阵分析的基础上给出的融合算法在不损失融合精度的情况下，计算所需的时间大大减少，较好地解决了这一问题。因此，该方法非常适用于处理能力有限的传感器结点，也满足了组网雷达防空对实时性和同步性的需求。

［1］陈永光，李修和，沈阳.组网雷达作战能力分析与评估［M］.北京:国防工业出版社，2006.

［2］邓勇，朱振福，钟山.基于证据理论的模糊信息融合及其在目标识别中的应用［J］.航空学报，2005，26(6):754-758.

［3］王加阳，周勇.冲突证据的融合方法研究［J］.计算机应用研究，2008，25(7):2046-2049.

［4］何友，王国宏，陆大纟金，等.多传感器信息融合及应用［M］.北京:电子工业出版社，2007.

［5］王洪峰，单甘霖，梅卫.基于证据理论的跟踪辅助目标识别［J］.电光与控制，2004，11(4):21-23.

［6］王林，寇英信.Dempster-Shafer证据理论在空战态势评估方面的应用［J］.电光与控制，2007，14(6):155-157.

［7］周中良，于雷，敬军.基于模糊理论的多传感器数据融合系统［J］.电光与控制，2007，14(2):23-25.

［8］宿陆，李全龙，徐晓飞，等.基于DS证据理论的传感器网络数据融合算法［J］.小型微型计算机系统，2006，26(7):1321-1325.

［9］LEUNG H，WU Jiangfeng.Bayesian and Dempster-Shafer target identification for radar surveillance［J］.IEEE Trans Aero Elect Sys，2000，36(2):432-447.

［10］LUCAS C，ARAABI B.Generalization of the Dempster-Shafer Theory:A fuzzy-valued measure［J］.IEEE Transactions on Fuzzy Systems，1999，7(3):255-269.