一种基于前馈网络的素数Sigma-Delta调制器优化设计*

王镇道，阮忠周

(湖南大学 物理与微电子科学学院，湖南 长沙　410082)



一种基于前馈网络的素数Sigma-Delta调制器优化设计*

王镇道，阮忠周†

(湖南大学 物理与微电子科学学院，湖南 长沙410082)

Sigma-Delta调制器是小数分频锁相环(Phase Locked Loop, PLL)中的关键模块，其噪声整形效果直接影响PLL的输出杂散、频率精度等性能.已有调制器均不能同时解决输出序列周期短、输出小数值无法覆盖0到1以及输出存在误差问题.针对这些问题，提出了一种新型的、基于前馈网络的素数调制器结构，使调制器的输出序列周期在任何输入值和初始值下都能达到M3，比传统调制器增大约M2/2倍，解决了已有调制器的输出序列周期短的问题，其中M为比2n0小的最大素数，n0为调制器中加法器的位数.提出的调制器还保证了输出小数值能够覆盖0～1、输出无误差.仿真结果表明，得益于输出序列周期更长，提出的调制器比已有的调制器更能有效去除输出量化噪声功率谱中的毛刺，噪声整形性能更接近理想调制器.

Sigma-Delta调制器；量化噪声；功率谱；前馈网络；素数

小数分频器是锁相环(Phase Locked Loop, PLL)频率综合器中的关键模块[1]，它解决了整数分频PLL中输出频率精度受限于输入参考频率的问题[2].传统的小数分频器是基于数字累加器，小数分频值α直接决定了累加器的输出y[n]的周期，使PLL的输出功率谱在距离中心频率α·fref处产生小数杂散，其中fref为PLL的输入参考频率[2].Sigma-Delta调制器凭借着优秀的噪声整形性能解决了小数杂散问题，被广泛地应用于小数分频PLL中[3-5].

然而，传统的Sigma-Delta调制器在某些特定输入下输出序列周期仍然很短，使调制器的输出量化噪声功率谱存在严重的毛刺，影响PLL输出杂散.通过对调制器的输入施加抖动可以有效地打乱调制器的输出序列，达到延长序列周期的效果[6-7].然而，在施加抖动的同时也引入了抖动噪声，拉高了调制器的输出噪底.针对这个问题，文献[8]在高阶调制器中添加额外的延迟单元，并对抖动噪声施加二阶高通滤波器，从而降低了低频处量化噪声的噪底，但该结构使原本为高通的量化噪声传输函数变成了带通[8].文献[9]对多级调制器中第一阶调制器设定奇数初始值来延长序列周期，但这种方式并不能显著地增长序列周期，并且即使调制器的阶数增加，序列周期长度仍然不变.文献[10]通过设定调制器中加法器的模值为素数，保证了调制器在任何输入下的序列周期均能达到该素数值，同样地，这种结构中仅第一阶调制器起到了延长序列周期的效果，第二阶及以上的调制器对输出序列周期无任何贡献.文献[11-12]在传统的一阶调制器上施加了额外的反馈，使输出序列周期随着调制器阶数的增加呈指数增长，但该结构的输出小数范围无法覆盖0～1，导致PLL的输出频率存在死区，此外，该结构的输出与设定值之间存在误差，引起PLL输出的频率偏差.文献[13]在多级调制器之间施加额外的前馈电路，较大程度上增长了输出序列周期，然而，当调制器输入为某些特定的数时，第一阶调制器输出序列周期很短，影响了整体的输出序列周期.

针对已有的Sigma-Delta调制器存在的这些问题，本文提出了一种改进的调制器结构，通过设定每一阶调制器中加法器的模值为素数，并在相邻阶数调制器之间施加前馈电路，不仅保证了输出小数范围能覆盖0～1，输出不存在误差，而且使调制器输出序列周期达到M3，比传统结构增大了约M2/2，其中M为比2n0小的最大素数，n0为调制器中加法器的位数.仿真结果表明，提出的调制器结构能更有效地消除量化噪声功率谱上的毛刺，噪声整形性能更接近理想调制器.

1　调制器结构

本文提出的调制器结构框图如图1所示，图中左边的虚线框内是模值M为素数的一阶Sigma-Delta调制器，即文献[10]中的一阶调制器，其中M为比2n0小的最大素数，n0为调制器中加法器的位数.与文献[10]不同的是，本文提出的调制器结构在相邻阶次的一阶调制器之间增加了前馈电路，该前馈网络把每阶调制器的输出与量化误差相加作为下一阶调制器的输入.右边虚线框内为噪声消除电路.e1[n]，e2[n]，e3[n]为3个量化器的量化噪声；y1[n]，y2[n]，y3[n]为3个一阶调制器的输出.3个一阶Sigma-Delta调制器在Z域的传输函数分别为：

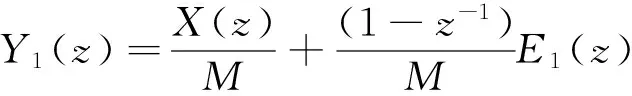
(1)

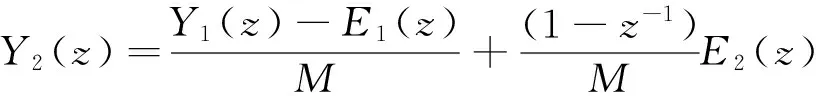
(2)

(3)

式中：E1[z]，E2[z]和E3[z]分别为-e1[n]，-e2[n]和-e3[n]的Z变换.

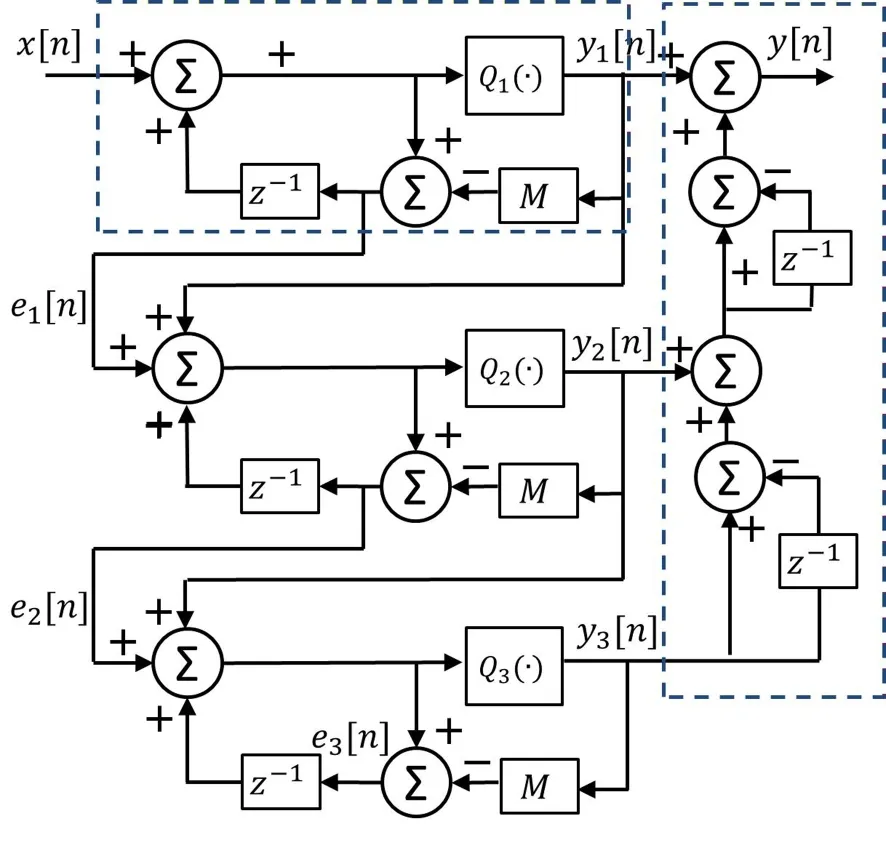
图1　调制器结构框图

噪声消除电路在Z域的传输函数为：

Y(z)=Y1(z)+(1-z-1)Y2(z)+

(1-z-1)2Y3(z).

(4)

最终可以得到：

Y(z)=STF(z)·X(z)+NTF(z)·E(z).

(5)

式中：

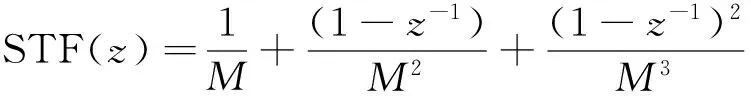
(6)

NTF(z)=(1-z-1)3；

(7)

(8)

从式(6)中可以看出，信号传输函数STF(z)包含了3个部分，分别是全通函数、一阶高通函数和二阶高通函数.由于Sigma-Delta调制器应用于小数分频器时，输入x[n]为常数，经过高通函数后得到的值为0，因此STF(z)中仅全通函数1/M对调制器的输出有贡献，即STF(z)=1/M.

量化噪声传输函数NTF(z)是三阶高通滤波器.把量化噪声e1[n]，e2[n]，e3[n]建模成独立的加性白噪声后，可得到理想情况下输出量化噪声的功率谱密度为：

(9)

其中：fn为归一化频率，取值范围为0～1.

2　调制器性能分析

Sigma-Delta调制器应用于小数分频器时，有3个关键性能需要考虑，分别是：

2)输出误差：为了使PLL的输出频率与设定值一致，要求调制器的输入值与输出小数值之间呈线性关系[13].因此调制器输入值为X时，输出的小数分频值应为X/N，其中N为调制器的模值.当输出小数值为X/N+λ时，则输出频率与设定值相差λfref.

3)输出序列周期：采用数字电路实现Sigma-Delta调制器时，调制器等效于一个有限状态机(Finite State Machine, FSM)，因此其输出序列周期是一个有限值[9].假设调制器的输出序列周期为L，则量化噪声的功率将会分布在L个点上.当L的数值很小时，会导致量化噪声输出功率谱出现严重的毛刺.因此，在设计调制器结构时，需要尽可能地延长输出序列周期.

2.1输出小数范围

在用数字电路实现Sigma-Delta调制器时，需要使用加法器实现高通函数和噪声消除函数[14].当累加器的输入大于2M时，累加器溢出.在本文提出的调制器结构中，x[n]，e1[n]，e2[n]，e3[n]的数值范围为0～M-1，前馈网络的取值范围是0～1，因此不存在加法器溢出问题.

表1列出了已有调制器和本文提出的调制器输入范围以及小数覆盖范围的对比，其中假设加法器的位数为n0，N的取值为2n0，M是比N小的最大素数.从表1中可知，HK-MASH结构的小数覆盖范围小于1，因此以HK-MASH结构为小数分频器的PLL输出频率将存在死区，而其他调制器结构的输出小数值均能覆盖[0, 1].

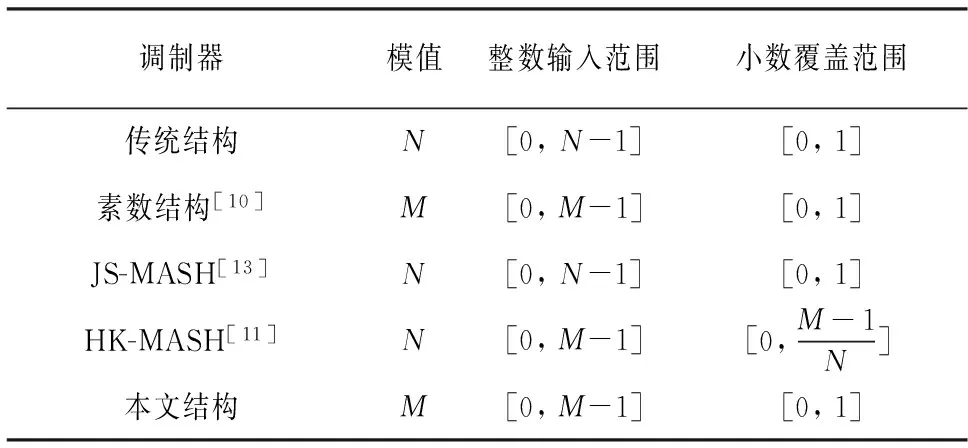
表1　调制器输入范围对比

2.2输出误差

在提出的调制器结构中，当输入值x[n]为常数X时，信号传输函数STF(z)为1/M，得到的输出小数值为X/M，因此调制器的输出与输入之间呈线性关系，不存在误差.表2列出了已有调制器和本文提出的调制器的输出误差对比.可以看出，除HK-MASH之外的调制器结构输出误差均为0，而HK-MASH的输出误差随着输入的增大而线性增大.

表2　调制器的输出误差对比

2.3输出序列周期

本文提出的三阶调制器结构是由3个一阶调制器级联得到的，其中一阶调制器的数学模型如图2所示.从图2中可以得到：

(10)

(11)

联立等式(10)和(11)可以得到：

(12)

因此，对于三阶调制器，得到如下3个等式：

(13)

(14)

(15)

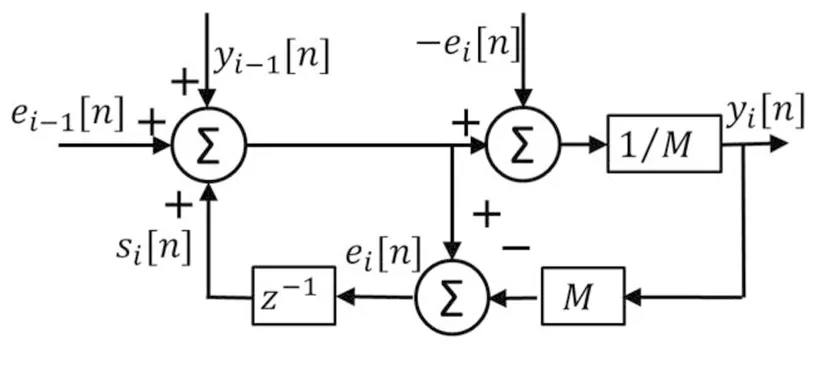
图2　一阶调制器数学模型

从图2中，还可以得出：

(16)

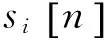
(17)

当i取值为1和2时，分别把等式(13)和(14)代入式(17)，可以得到式(18)和(19)：

(18)

s2[0])modM}/M.

(19)

对式(13)和(14)的左右两边分别进行求和，得到式(20)和(21)：

(20)

(21)

设调制器的输出序列周期长度为L，则对于e3[n]，等式(22)必然成立.

e3[L]-e3[0]=0

(22)

通过联立式(18),(19),(20),(21)和(22)，可以得到式(23).

(23)

其中：

(24)

其中:

由于X的取值范围是0到M-1，为了使式(24)等于0，即满足式(22)这个条件，K1必须取M的整数倍，所以原假设K1不为M的整数倍不成立.重新假设K1=K2M，即L=K2M2，并代入式(23)可得：

e3[L]-e3[0]=K2XmodM.

(25)

表3列出了已有调制器和本文提出的调制器的输出序列周期对比，传统结构和素数结构的输出序列周期长度都很短，JS-MASH结构的输出序列周期长度的最大值与最小值之间差别较大，其最小值远小于HK-MASH和本文提出的结构的最小值.而本文提出的调制器结构和HK-MASH都能保证输出序列周期在任意输入和初始值下均达到M3.

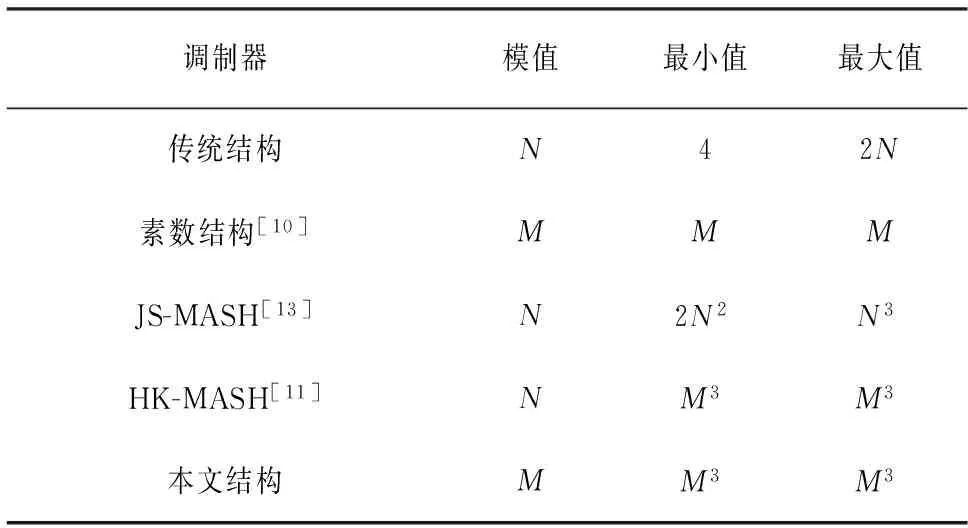
表3　调制器的输出序列周期对比

综上所述，在输出序列周期长度方面，只有本文提出的结构和HK-MASH才能保证在任何输入和初始值下均达到一个稳定的、足够长的数值.而其他调制器在某些特定输入时存在输出序列太短问题.但HK-MASH的输出小数范围无法覆盖0～1，且输出误差随着输入的增大而增大，而本文提出的调制器结构均不存在这些问题.

3　调制器的性能仿真

Sigma-Delta调制器应用于小数分频器时，在特定的带宽内，量化噪声总功率为定值.输出序列周期长度越大，量化噪声功率分布越广泛，输出量化功率谱也越平滑.输出序列周期达到一定数值时，才能有效地消除量化噪声功率谱上的毛刺.

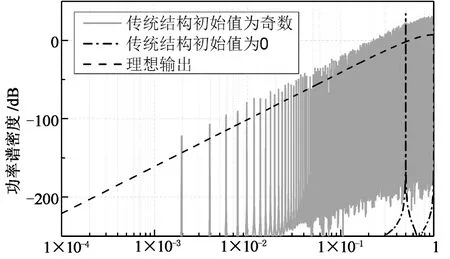
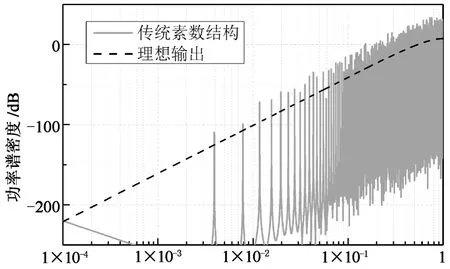
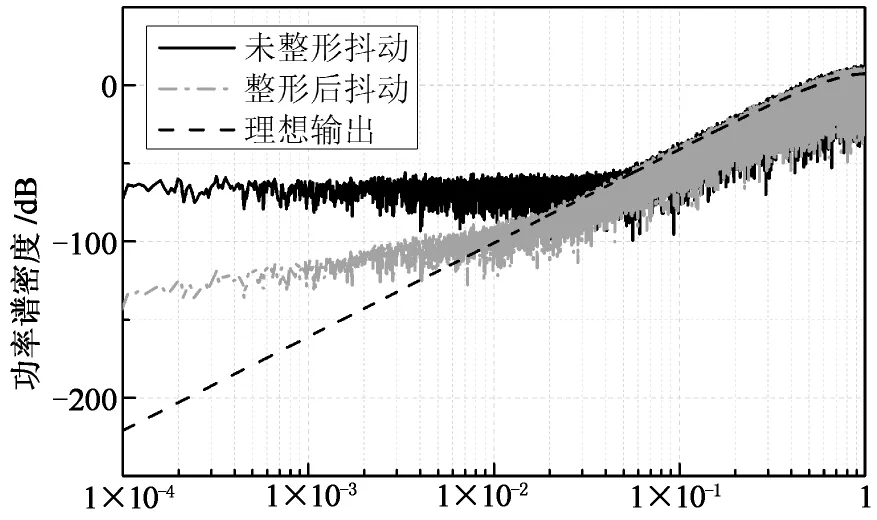
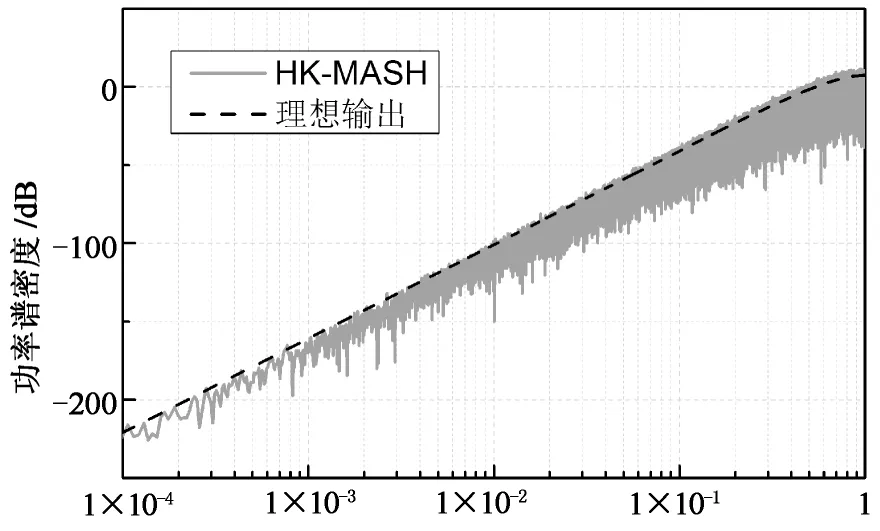
图3是已有调制器和本文提出的调制器的输出功率谱，这些功率谱都是在加法器为9位，输入值为256的情况下得到的.图中的虚线为理想情况下的输出量化噪声功率谱，是通过把量化噪声建模成理想白噪声后，再乘上噪声传输函数得到的.

从图3中可以看出，在传统结构中，倘若不采取任何措施，量化噪声功率谱只有两个毛刺，在设定初始值为奇数后，噪声功率谱得到了较大的改善.同样地，设置调制器的模值为素数也在一定程度上改善了噪声功率谱密度的毛刺问题.然而由于采用这两种方法时，输出序列周期仍然较小，无法有效平滑量化噪声功率谱.施加抖动可有效地解决功率谱上毛刺的问题，但同时也使噪底大大增大.尽管对抖动进行一阶高通整形后，可使噪底降低，但与理想的噪声功率谱仍然相差较远.与前面所述的几种方法相比，JS-MASH结构的调制器在很大程度上减小了功率谱上毛刺的大小，但由于输入值是加法器模值的一半，第一阶调制器的输出序列周期长度仅为2，最终导致JS-MASH的输出序列周期长度仅达到524 288，仍然无法有效地平滑量化噪声功率谱.而本文提出的结构和HK-MASH的输出序列长度都达到了131 872 229，远大于JS-MASH结构及其他结构的输出序列周期长度.从图3(e)和(f)中可以看出，本文提出的结构和HK-MASH都能有效地消除毛刺，达到平滑噪声功率谱的效果，并且二者的效果相当，性能接近理想调制器.然而HK-MASH的输出小数范围无法覆盖0～1，且存在输出误差问题，而本文的结构中均不存在这些问题.

归一化频率

归一化频率

归一化频率

归一化频率

归一化频率

归一化频率

在PLL频率综合器应用中，为了防止小数杂散的产生，Sigma-Delta调制器必须能够在所有的输入值下都具有平滑、无毛刺的输出功率谱.图4为本文提出的调制器在加法器为9位，模值为509的情况下得到所有输入值下的输出量化噪声功率谱.从图4中可以看出，调制器在所有的输入情况下，输出噪声功率谱均是无毛刺、平滑的，满足频率综合器的要求.

图4　提出的调制器在所有输入下的输出功率谱

4　结　论

针对已有调制器无法同时解决输出序列周期短、输出存在误差、输出小数覆盖范围小的问题，提出了一种新型的调制器结构，该结构采用了素数作为加法器的模，并在相邻阶数调制器之间增加了前馈网络，保证了调制器输出小数范围能够覆盖0～1，且输出值与设定的小数值完全一致，不存在误差.文中还建立了调制器的数学模型，证明了该调制器在任何输入值和任何初始值下的输出序列周期长度都能达到了M3，克服了已有结构输出序列周期短的问题，其中M为比2n0小的最大素数，n0为调制器中加法器的位数.仿真结果表明，得益于输出序列周期更长，提出的调制器比已有的调制器更能有效地去除Sigma-Delta调制器输出量化噪声功率谱中的毛刺，噪声整形效果更接近理想调制器.

[1]晏敏, 徐欢, 乔树山, 等.小数分频频率合成器中Σ-Δ调制器设计与实现 [J]. 湖南大学学报:自然科学版, 2014, 41(10): 91-95.

YAN Min, XU Huan, QIAO Shu-shan,etal. Design and implementation of Σ-Δ modulator in fractional-N frequency synthesizer [J]. Journal of Hunan University: Natural Sciences, 2014, 41(10): 91-95.(In Chinese)

[2]PIN-EN S, PAMARTI S. Fractional-N phase-locked-loop-based frequency synthesis: a tutorial [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2009, 56(12): 881-885.

[3]VENERUS C, GALTON I. Delta-Sigma FDC based fractional-N PLLS [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(5): 1274-1285.

[4]KENNEDY M P, HONGJIA M, FITZGIBBON B,etal. 0.3-4.3 GHz Frequency-accurate fractional-N frequency synthesizer with integrated VCO and nested mixed-radix digital Δ-Σ modulator-based divider controller [J]. IEEE Journal of Solid-State Circuits, 2014, 49(7): 1595-1605.

[5]JAEWOOK S, HYUNCHOL S. A 1.9-3.8 GHz ΔΣ fractional-N PLL frequency synthesizer with fast auto-calibration of loop bandwidth and VCO frequency [J]. IEEE Journal of Solid-State Circuits, 2012, 47(3): 665-675.

[6]GONZALEZ-DIAZ V R, GARCIA-ANDRADE M A, FLORES-VERDAD G E,etal. Efficient dithering in MASH Sigma-Delta modulators for fractional frequency synthesizers [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2010, 57(9): 2394-2403.[7]KENNEDY M P, FITZGIBBON B, DOBMEIER K. Spurious tones in digital delta sigma modulators with pseudorandom dither [C]// Proceedings of IEEE International Symposium on the Circuits and Systems(ISCAS).Beijing: IEEE,2013:2747-2750.

[8]FITZGIBBON B, PAMARTI S, KENNEDY M P. A spur-free MASH DDSM with high-order filtered dither [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2011, 58(9): 585-589.

[9]BORKOWSKI M J, RILEY T A D, HAKKINEN J,etal. A practical Σ-Δ modulator design method based on periodical behavior analysis [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2005, 52(10): 626-630.

[10]HOSSEINI K, KENNEDY M P. Mathematical analysis of a prime modulus quantizer MASH digital Delta-Sigma modulator [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2007, 54(12): 1105-1109.

[11]HOSSEINI K, KENNEDY M P. Maximum sequence length MASH digital Delta-Sigma modulators [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2007, 54(12): 2628-2638.

[12]HOSSEINI K, KENNEDY M P. Architectures for maximum-sequence-length digital Delta-Sigma modulators [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(11): 1104-1108.

[13]JINOOK S, IN-CHEOL P. Spur-free MASH Delta-Sigma modulation [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2010, 57(9): 2426-2437.

[14]CHIA-YU Y, CHIH-CHUN H. Hardware simplification to the delta path in a MASH 111 Delta-Sigma modulator [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2009, 56(4): 270-274.

An Optimal Design of Prime Sigma-Delta Modulator Based on Feed Forward

WANG Zhen-dao, RUAN Zhong-zhou†

(School of Physics and Electronics, Hunan Univ,Changsha, Hunan410082, China)

As the key module of fractional-N PLL(Phase Locked Loop), the Sigma-Delta modulator can significantly improve the performance of the fractional-N PLL by the way of noise shaping. However, when it comes to the three most important specifications: the output sequence cycle, the range and the error, the now existing modulators cannot improve them at the same time. As a contrast, the proposed novel Sigma-Delta modulator ameliorates the aforementioned three specifications simultaneously by adding a feed forward between two adjacent stages and adjusting the modulus of adders to prime number. Regardless of the input value and initial conditions, the presented modulator guarantees a sequence length of M3, which is almost M2/2 times of that in traditional modulator, whereMis the largest prime number smaller than 2n0,andn0is the bit width of adders. The simulation results show that, compared with the existing modulators, the proposed modulator can effectively remove the spur in the output spectrum and make it more close to the ideal Sigma-Delta modulator.

Sigma-Delta modulator; quantized noise; power spectrum; feed forward; prime number

1674-2974(2016)08-0108-07

2015-06-15

湖南省科技计划资助项目(2014FJ3155)

王镇道(1974-)，男，湖南益阳人，湖南大学副教授，博士†通讯联系人，E-mail:laoruan@hnu.edu.cn

TN74

A