“人在回路”制导链路仿真
刘 琨,贺知明
(电子科技大学电子工程学院,四川 成都 611731)
0 引言
面对日益复杂的威胁环境,要求战术导弹末制导具有能够自主、智能识别目标的能力。但由于识别目标需要计算的数据量很大,不管是计算速度,容量和算法实现起来都很困难。为此,精确制导导弹引入了“人在回路”电视末制导。导弹上的电视导引头获取到目标和背景图像后,通过上行数据链传输到发射平台进行处理显示,控制人员根据图像选择控制指令,控制指令再通过下行数据链传输到导弹的控制器上,导弹即按收到的指令运动和攻击目标。可以看到“人在回路”制导链路实际上是双向信息传输链通信系统。系统框图如图1所示。
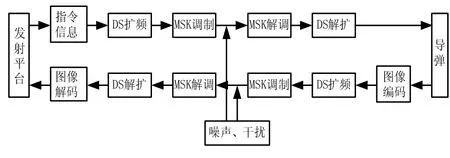
图1 双向信息传输链通信系统
1 系统设计
1.1 图像处理
导弹一般打击的目标比较单一,目标的颜色和轮廓也比较明显,使用黑白电视图像就能清楚识别。但这样也面临处理巨大的数据量,花费很大的传输带宽。因此需要采用数字视频压缩技术。加装摄像头的导弹高速运动,一些基于运动补偿压缩技术的编码效果并不明显,反而会增加处理时间,而从该系统要求视频图像的连续性和实时性来说,对连续视频的每一帧均采用JPEG2000编码的JPEG2000更适合[1]。
首先将图像分割成大小相等、相互不重叠的矩形图像片(Tile)。然后进行直流电平位移操作,目的是去掉图像片中直流分量,从而使小波变换后系数取正、负值的概率基本相等。接着每个图像片进行正向离散小波变换(DWT)。它的实质是把原始图像的像素值矩阵变换成另一个有利于压缩编码的系数矩阵。该系统采用了CDF9/7滤波器进行6层小波分解。变换后,系数的总量并未减少,要真正地压缩数据量,还要对其进行量化,编码[2]。由于量化可通过块截断有效控制,因此子带b的量化步长的选择并不如想象中那样严格[3]。一般量化步长。其中Δ是基本量化步长,可通过调整它来实现所需要的整个压缩码率或失真级别。一般取Δ= 2-R,R为经过分量变换后系数的比特位深。G 是能量增b益因子,并近似为 G≈22db,d代表子带b所在的小波变换bb级数。为方便,引入标记χb[n]∈{-1,1},且,以及,则量化索引。最后将量化后的各子带分割成互不相交的矩形编码块,分别对每个码块进行编码。JPEG2000选用了EBCOT嵌入式编码方法。使用两层编码策略[4]。第一层编码对码块内的小波系数进行嵌入式码块编码,第二层编码使用码率控制算法打包比特流。在接收端,图像的解压缩解码基本是压缩编码的逆过程。
1.2 扩频与调制系统
从隐蔽性和抗干扰的角度,该系统选择了直接序列扩频和最小键控频移调制体制。在扩频系统中,发射端用伪随机码(PN)将载有信息的信号扩展到某个较宽的带宽上,然后在信道上进行传输。当这个接收信号乘以一个与发射端同步了的PN码信号时,所期望的信号被解扩回到窄带带宽上,而其它干扰信号都被扩频到一个较宽的带宽内。这样通过接收端的滤波器就能得到期望信号。另外,任何不具有该 PN码序列的其他接收机不可能解出这个信号[5]。扩频后的信号经过最小移频键控(MSK)调制发射。MSK是二进制连续相位频移键控(FSK)的一种特殊形式,其频差是满足两个频率相互正交的最小频差,并要求FSK信号的相位连续[6]。其频差式中,Ts为输入数据流的比特宽度。其中,xk是为了保证,时相位连续而加入的相位常量。在给定的频带内,MSK能比2PSK的数据传输速率更高,且在带外的频谱分量要比2PSK衰减的快[7]。
1.3 MATLAB仿真
对于上行链路,图像源采用一幅512×512标准测试灰度图像“Lenna”,如图2(a)所示。在实际硬件电路中,如果时钟为8.33 MHz,完成一幅图像的压缩时间为65 ms。小波压缩解压缩芯片(如ADV202)可实现压缩比达350~400∶1。该仿真中设置图像压缩比为350:1,这样码元速率约为Rb1=300Kb/s。采用Matlab结合Jasper软件来实现JPEG2000的编解码。解码后图像如图2(b)所示。

图2 原始图像和解压后图像
然后进行DS扩频。扩频过程就是和PN码进行逐码片逻辑异或。选用gold码[8],码长为128bit。经过DS扩频后,码元速率变为 Rc1×128 =38.4Mb/s,则扩频带宽 B1约为80 MHz。设工作频率 fc1为20 GHz,码元宽度 Ts1=1/ Rc1≐ 2 .6×10-8s。再将单极性码元变为-1,+1的双极性码元并送入MSK调制发射。在信道中加入高斯白噪声及噪声调幅干扰[9],如图3所示。接收到的信号经过MSK解调,解扩及图像解码,即可获得重构后的图像。
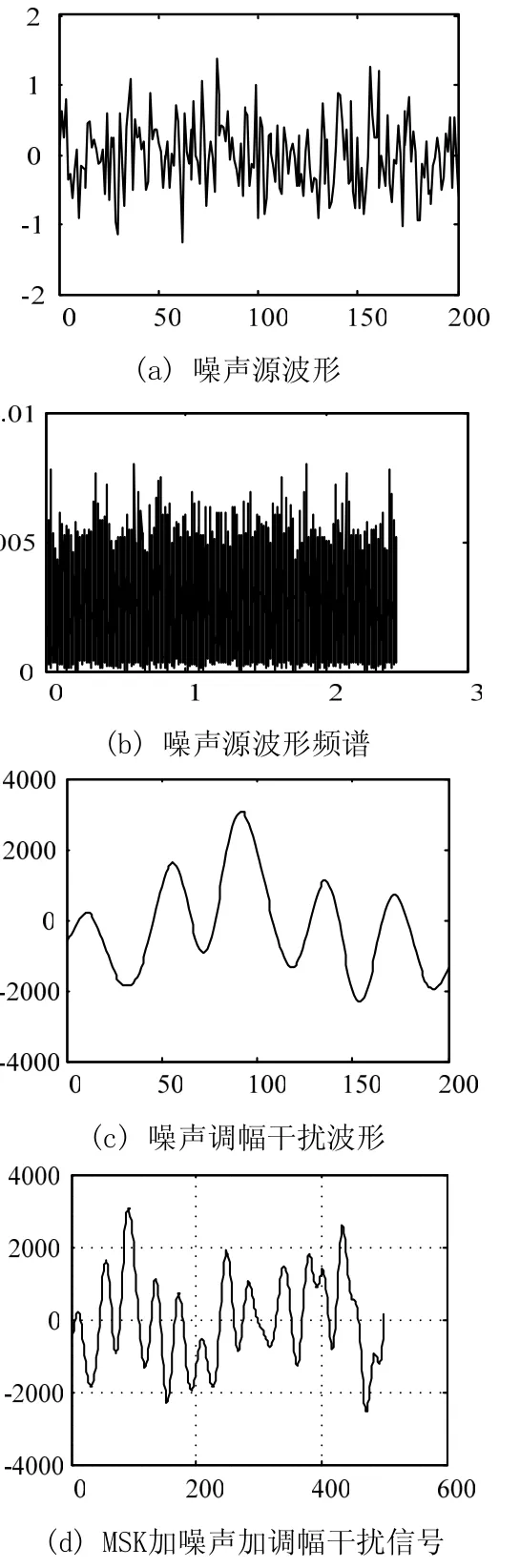
图3 噪声及干扰信号
对于下行链路,实现方式与上行链路基本相同。只是由randsrc命令生成1,0单极性码的信源,以此来模拟发射指令。武器系统要求导弹控制指令传送码率为 Rb2= 1 2.8Kb/s,gold码长度选为512bit,则扩频后码元速率Rc2= Rb2×512 = 6.55Mb/s,则扩频带宽 B2约为13 MHz。工作频率 fc2设为3 GHz,码元宽度 Ts2=1/ Rc2≐ 1 .5×10-7s。
2 性能分析
2.1 干扰容限
干扰容限,是指在保证系统工作正常的条件下,接收机能够承受的干扰信号比有用信号高出的分贝数,干扰容限直接反映了扩频系统接收机可能抵抗的极限干扰强度,用jM表示,单位为dB[10]。

式(1)中,Ls为扩频系统解扩解调的固有处理损耗,它是扩频信号处理以及工程实现中的误差对信号造成的损伤而引起的; ( S/N )out为系统正常工作时要求的最小输出信噪比;GP= ( Rc/ Rb)为系统的处理增益; Rb为信息速率; Rc为伪码速率。则上下行链路处理增益分别为 Gp1= 2 1 dB ,Gp2= 2 7 dB 。假设进入基带解调器的最小输出信噪比(S/ N )out= 1 0 dB ;处理损耗 Ls= 3 dB ,将上述参数代入式(1),得上行链路干扰容限 Mj1= 8 dB ;下行链路干扰容限Mj2= 1 4 dB 。计算结果说明,要提高扩频系统的抗干扰能力,就应该提高扩频系统的处理增益,即可以采用更高位数的扩频码以提高伪随机码的速率。当处理增益提高到一定程度时,不能再靠提高伪随机码速率的方法来提高系统的处理增益,而应考虑用别的办法,比如可以降低信息速率。
2.2 误码率
采用Monte Carlo仿真说明了系统在抑制调幅干扰方面的有效性。对于每个SNR值,发送符号的个数N=10 000。图4给出了对于扩频码位数为128,在3种不同的调幅干扰下所得的仿真结果。图中还给出当除掉这个干扰时所测得的误码率。在这些仿真过程中,加性噪声的方差都保持不变,产生两种干扰的高斯白噪声的方差也不变。
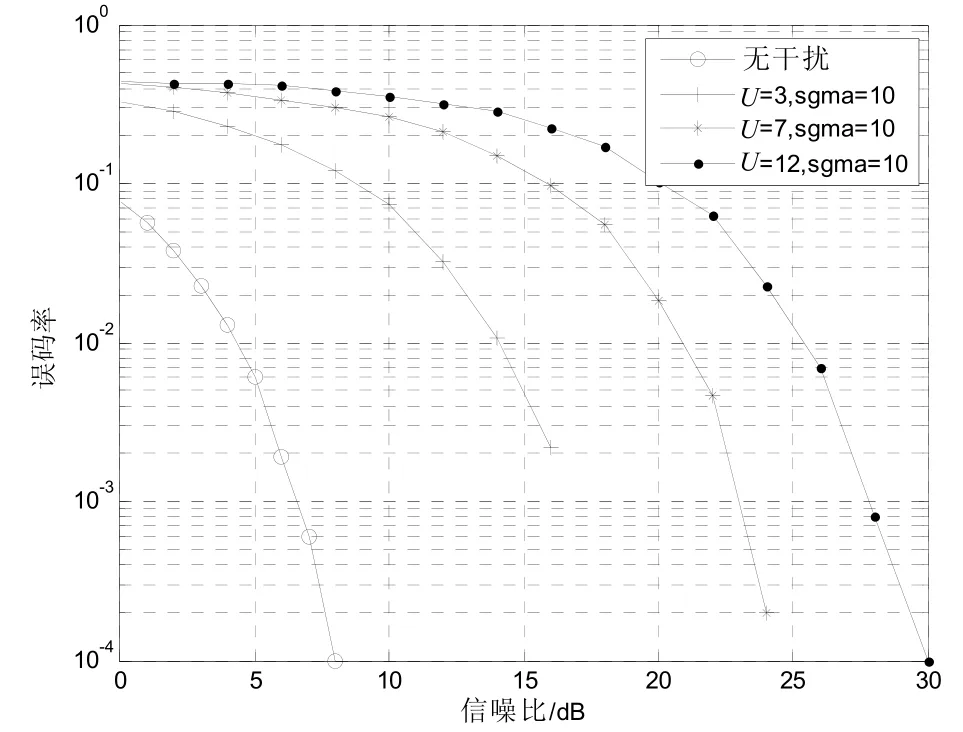
图4 系统的误码率
从图4中可以看到,在无干扰的情况下,即使是在信噪比很小的条件下,扩频系统的误码率依然很低。加了干扰以后,特别是在大功率的扰下,随着信噪比的增加,误码率会缓慢减小。可以看到扩频系统的抗干扰性能还是很强的。
3 结语
根据“人在回路”制导链路的工作原理提出了一种图像制导加 DS-MSK通信体制的双向通信链路的建模方案并用MATLAB编程实现[11]。从而建立了一种简单且有效的信息传输链路。由于联系导弹和后方载体平台的数据链回路工作距离可达几百至上千公里,是一个容易被干扰的环节[12]。因此程序中预留了干扰的接口,这样就可利用此模型进一步研究数据链的抗干扰性能或寻求破坏制导链路通信的突破口。另外链路中为了仿真方便没有涉及差错控制编码的内容,需要完善。
[1] 栾宪锋.基于M-JPEG2000的电视制导图象压缩系统研究[D].哈尔滨:哈尔滨工业大学,2006.
[2] 张德丰.MATLAB数字图像处理[M].北京:机械工业出版社,2009.
[3] TAUBMAN D S,MARCELLIN M W.JPEG2000图像压缩基础、标准和实践[M].北京:电子工业出版社,2004.
[4] 全子一.图像信源压缩编码及信道传输理论与新技术[M].北京:北京工业大学出版社,2006.
[5] PROAKIS J G,SALEHI M,BAUCH G.现代通信系统[M]. MATLAB版.北京:电子工业出版社,2005.
[6] 高凯,王世练,刘毅坚,等.直扩MSK中频数字化相干接收的设计与实现[J].通信技术,2002,42(09):21-22.
[7] 张辉,曹丽娜.现代通信原理与技术[M].西安:西安电子科技大学出版社,2002.
[8] 韦岗,季飞,傅娟.通信系统建模与仿真[M].北京:电子工业出版社,2007.
[9] 胡修林,熊小兰.典型压制性干扰的建模与仿[J].雷达与对抗,2006(04):10-12.
[10] 黄峥,李科杰,金连宝. 电视图像遥控制导小型战术导弹无线电双向信息传输链路的研究[J].导弹与制导学报,2000(04):5-11.
[11] 谢晓燕,宁永海. 基于MATLAB的通信系统仿真应用研究[J].通信技术,2007,40(12):82-83.
[12] 鲍虎,刘隆和.对“人在回路中”末制导导弹的干扰研究[J].航天电子对抗,2001 (02):1-2.

