基于软限幅法降低峰均比的性能分析

苏雁泳，吴华明，徐媛媛

（哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨 150001）

0 引言

在无线移动通信中，要求提供高速率和高质量的通信服务。OFDM 是一种无线环境下的高速多载波传输技术，它能有效地抗多径衰落，具有非常高的频带利用率，适于宽带移动通信，是下一代移动通信系统中实现高速移动通信的最有前途的技术。由于OFDM符号是由多个统计独立的经过调制的正弦子载波信号相加而成的，合成的OFDM信号有可能产生比较大的峰值功率，由此会带来较大的峰均功率比(PAPR)。大的峰均功率比会带来很多问题，比如增加A/D转换器和D/A转换器的复杂度，降低射频功率放大器的有效性等。因此，如何有效地降低OFDM系统PAPR是目前OFDM系统研究的一个主要问题。当接收到的信号较弱时，采用选择性映射法(SLM)和部分传输序列法(PTS)虽然能够改善系统的误码性能，但是，效果不是很好，且系统复杂[1-2]。采用编码技术是可以有效地降低OFDM系统的峰均比，但在子载波数很大时，编码效率很低[3]。为此，提出了基于软限幅法来降低 PAPR，其能够改善 OFDM 系统的误码性能，且传输效率高、易于实现。

1 OFDM系统互补累积函数分布特性的分析

OFDM 系统的并行多载波调制是用基带的快速傅立叶变换(IFFT)算法来实现的，其基带的等效IFFT实现表达式为：由式(1)可知，任一个OFDM符号是由N个离散信号组成的，式中的s(n)表示该OFDM符号中的第n个样值。在OFDM系统中，对于离散信号，峰均功率比(简称为峰均比)PPAPR定义为：

由式（2）可知，降低PAPR可通过对具有较大样值的s(n)信号进行限幅来实现。

OFDM 信号幅度是各子载波信号的叠加，当子载波数为128时，采用不同方法降低PAPR的互补累积分布函数[4]，如图1所示。

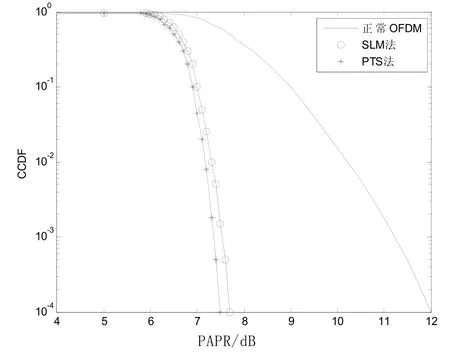
图1 不同方法的互补累积分布函数曲线

由于OFDM符号是由多个统计独立的经过调制的正弦子载波信号相加而成的，当子载波数较大时，其互补累积分布函数值服从高斯分布，小信号出现的概率较大，信号越大，其出现的概率越低。由图 1中正常峰均比互补累积分布函数(CCDF)曲线可知，虽然大信号出现的概率很小，但其模值很大，从而系统的峰均比很大。由于输入到功率放大器等模块的信号具有较大的动态范围，且大信号出现的概率很低，从而，造成系统的信噪比难以提高，通信系统的误码率较大。为了提高系统的信噪比，降低信道传输噪声对系统误码性能的影响，希望系统PAPR设定值越小越好，这样小信号的输出功率增加，从而使系统的平均输出功率增加。但是，大信号的畸变会越来越严重，从而造成系统误码率上升，二者相互矛盾。当信道传输噪声和信号畸变对系统的误码性能影响力相同时，系统的误码率最小。当OFDM系统功放模块的输出功率能力越强，接收到的信号信噪比越大，则传输噪声对系统的影响减小，要想使系统具有最小误码率，则PAPR值应取得大一些，反之亦然。当OFDM系统功放模块的输出功率能力较弱时，PAPR的取值应较小，此时，由图1可知，即使采用SLM法和PTS法，系统的信号畸变也会较严重，同时，还会使功率放大器等模块处于非线性工作状态，造成较严重地带内失真和带外干扰，以致造成系统误码率的提高和器件的损坏，且其算法复杂[5]。为此，提出了软限幅法来降低OFDM系统的PAPR。

2 软限幅法降低峰均比的原理

采用采用软限幅法来降低PAPR的原理方框图，如图2所示。

图2 基于星座映射法降低PAPR的原理

对于OFDM系统，首先对输入的二进制数进行星座映射（即数据调制），使二进制时域数字信号变成频域信号，进一步将输入的串行信号变成并行信号输出，并行路数N与OFDM系统的子载波个数相等，因此OFDM系统的符号长度也为N。接着，将并行数据送入IFFT变换模块，变换后得到的时域信号的长度也为N。由于多径时延造成符号间干扰，所以为了减少符号间干扰应插入循环前缀，循环前缀为变换后该符号的后M个数值，因此实际发送的符号长度为N+M。然后，将该并行数据进行并/串变换，并经过低通滤波实现数模转换，将得到的模拟信号送入上变频器进行频率搬移，最后，送入信道。此为OFDM系统的发射过程，接收过程为其的逆过程。假设OFDM系统的子载波个数为N，由于引入的循环前缀为N个子载波进行IFFT变换后的该符号的后M个数值，所以研究降低峰均比的问题时，只需考虑如何降低IFFT变换后得到的N个离散信号中那些超过系统线性工作范围的信号即可。采用软限幅法来降低峰均比只是在原有的OFDM发射子系统的IFFT模块后面加入了一个软限幅模块，对OFDM系统中那些超过系统线性工作范围的离散信号进行软限幅，确保系统工作在线性区间内，而其不像传统的限幅法采用限幅器件对调制后的射频信号进行限幅。由于其不需要采用非线性器件，因此，不会带来带内失真和带外辐射，能够确保系统可靠地传输。

软限幅法的工作流程，如图3所示。

由图3可知，其通过软件判决来限制系统所传输的信号样值在相应的动态范围之内。首先，对输入的二进制数据进行组帧和数字调制；接着，对该帧数据进行IFFT变换，并将计数器清零；然后，判断变换后的数据帧中的离散信号样值是否超过限幅门限；如果OFDM符号中的某离散样值 ck+ jdk的模值大于限幅门限电平时，则对该样值的实部和虚部进行等比例限幅，即将 ck和 dk分别乘以一个相同的系数k′= MN′，其中 M为限幅门限，N'为该离散样值的模值，k′＜ 1；否则，不对该离散样值进行限幅，计数器加1。最后，判断计数器值是否为N，如果为N，表示该帧数据软限幅完成，可对下一帧数据进行处理。采用软限幅法的优点是：可确保限幅后的OFDM符号中的数据值不会超过系统允许输入信号的最大值，且易于随意改变限幅门限M，即PAPR的设定值。

图3 软限幅流程

3 仿真结果与性能分析

采用Matlab仿真软件对软限幅法降低峰均比的方法进行仿真分析。系统子载波数为N=128，即OFDM符号的长度为128，子载波带宽为2 kHz，采用QPSK调制方式。仿真结果，如图4所示。

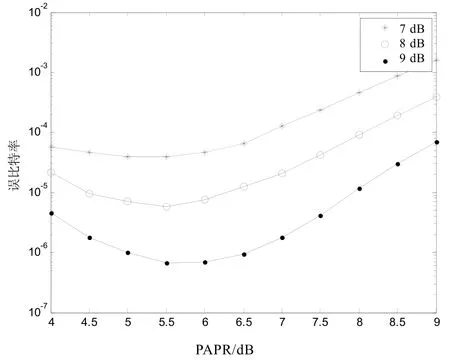
图4 不同信噪比、不同PAPR条件下，系统误码率特性曲线

图4中的三条曲线是分别表示：在PAPR为9 dB时，系统信噪比分别为7 dB、 8 dB和 9 dB时，系统误码率与 PAPR之间的关系曲线。随着软限幅门限的降低，即PAPR取值的减小，进入到接收系统的传输噪声减小、系统的信噪比增大，系统的误码率大大地降低，误码性能获得较大地改善，当PAPR的取值进一步减小时，信号畸变对系统误码率的影响增大，误码率增大。当接收到的信号较强时，如9 dB曲线，PAPR取值为5.7 dB 左右时，其系统误码率最小。而当接收到的信号较弱时，如7 dB曲线，PAPR取值为5.3 dB 左右时，其系统误码率最小。由图 4可知，随着接收到信号的强度的减弱，图中相应曲线的系统误码率最小值出现处的PAPR值越小。

4 结语

综上所述，当接收到的信号较弱时，采用目前被广泛关注的SLM和PTS方法的系统误码性能与采用软限幅方法相比较，二者误码性能接近。同时，采用SLM和PTS方法，会存在大量地OFDM符号，其动态范围超出功率放大器等模块的线性工作区间，从而带来带内干扰、频带弥散等的负面影响；并且，还要确保加权系数等信息能够被可靠的传输，且算法较复杂。而采用软限幅法来降低 PAPR，能够有效地改善 OFDM 系统的误码性能；同时，能够确保输入到功率放大器等模块的信号在相应的线性工作区间内，从而避免了带内干扰、频带弥散等的负面影响。系统不需要加入冗余码，传输效率高，且系统简单、易于实现。因此，该方法更具实用性。

[1] 林爱英,朱连轩,王敏杰.用选择性映射法减小OFDM信号的峰均比及其改进方法[J].电子科技,2006(09):26-28.

[2] 王林,江秀萍.降低OFDM信号峰均比的PTS技术[J].计算机工程与应用,2007,43(05):153-158.

[3] SATHANANTHAN K, TELLAMBURA C. Coding to Reduce both PAR and PICR of an OFDM Signal[J].IEEE Communications Letters,2002,6(08):316-318.

[4] 刘明攀.OFDM 信号限幅滤波的性能分析[J].通信技术,2009,42(11):10-12.

[5] 吴法文,胡茂凯,陈西宏,等.优化OFDM系统峰均比的PTS改进算法研究[J].通信技术,2009,42(11):13-15.