基于假设坐标系法的长定子直线同步电机无速度传感器算法

王 飞 葛琼璇

（中国科学院电工研究所 北京 100190）

1 引言

长定子直线同步电机因为其效率高、爬坡能力强、转弯半径小等优点被应用于磁悬浮列车和一些城市轨道列车中作为驱动装置。高性能的旋转电机控制策略如磁场定向、直接转矩控制等也被用于直线电机的控制系统中，如磁场定向控制已被成功应用于德国的TR系列磁悬浮列车牵引控制中。

磁悬浮列车采用磁场定向控制驱动电机，必须要获知车体的位置和速度信息，这也是列车为保证高速状态下的安全运行所必需的状态参数。在实际系统中，列车的位置信息及其他运行参数是通过车载设备检测，并以固定的频率无线传输给地面控制中心[1]。这种方式传输范围有限，需要沿着轨道建立地面基站，而且当列车运行速度增大时，固定的发送间隔中列车位置有很大变化，从而会使位置信息产生延迟，对列车的牵引控制以及运行安全产生不利影响。如果在控制单元中使用无速度传感器算法，通过定子的电压和电流来实时计算出动子位置，则可以减小信息的传输延迟，从而提高驱动控制的有效性以及系统的安全性。

本文所提出的无速度传感器算法利用任意旋转坐标系（假设坐标系）上的电机方程构造扰动观测器计算反电动势，并利用反电动势通过反三角函数获得该坐标系与实际dq坐标系之间的角度偏差，通过修正该偏差来获得位置和速度信息。整套算法在IOWorks环境中开发，并在基于 VME总线的控制系统中进行了实验验证。

2 电机模型

同步旋转坐标系 dq轴中长定子直线同步电机的电压动态方程为[2-5]

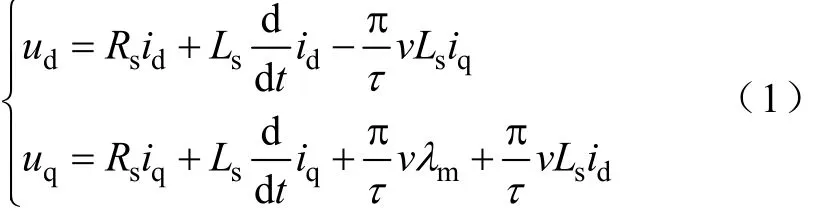
式中Ls,Rs——定子自感和电阻；

λm——动子磁链；

τ——定子极距；

v——动子线速度，其与同步电角速度ω的关系为/vτω=π。

运动方程为

式中m——电机质量；

Fx——直线电机的牵引力；

Fl——负载阻力；

kw——风阻系数。

以上数学模型是电机中各变量的基波方程，由于长定子直线电机动子长度有限，在动子两端截面会有较大漏磁通产生，存在端部效应，会对牵引力产生扰动。这种扰动往往在动子长度相对较短时较为明显，当动子侧极数较多而且在端部采用半极距时可以忽略[6]。

3 假设坐标系法

由图1所示，电机动子位置角度用动子磁通正向（d轴）与A相定子绕组轴线之间角度来表示。在无位置和速度传感器应用中该位置为未知量，用估算得到的θe来表示假设旋转坐标系δγ的位置，ωe来表示其电角速度，并设δγ坐标系与实际dq坐标之间的角度误差为Δθ。考虑到电压方程的时间常数远小于运动方程时间常数[7]，在δγ坐标系的电压方程中设估算速度已收敛到实际速度，且在一个电流采样周期内为常数[8]：

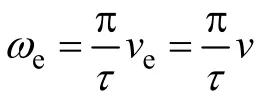
δγ 坐标系里的电压方程为

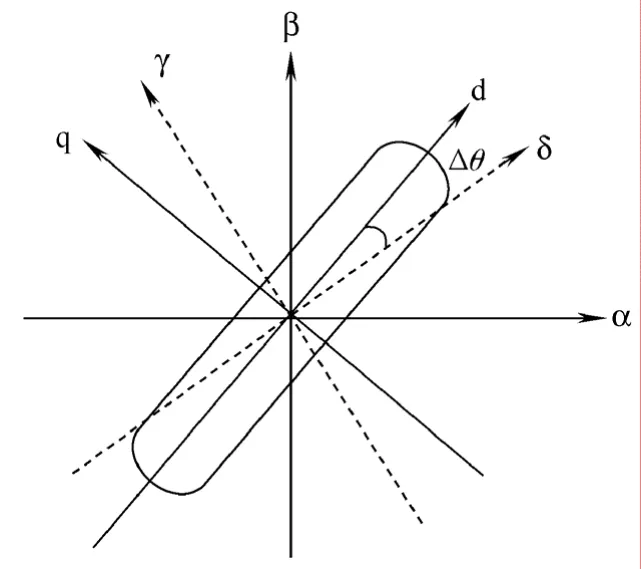
图1 dq与δγ坐标系Fig.1 dq and δγ reference frame

将上式矢量方程分解到δγ坐标轴上

设其中反电动势分量为

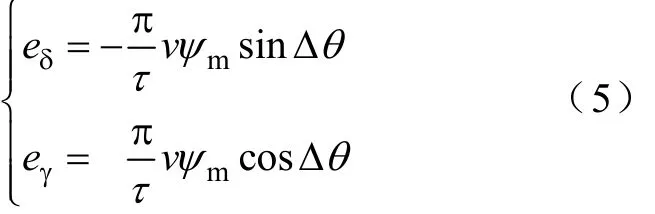
由式（5）可得角度误差Δθ可以通过eδ和eγ做反三角函数来获得。式（4）为以电流为状态变量的线性方程，反电动势分量在其中作为扰动量。因此可以构造扰动观测器来估算获得反电动势分量。扰动观测器为

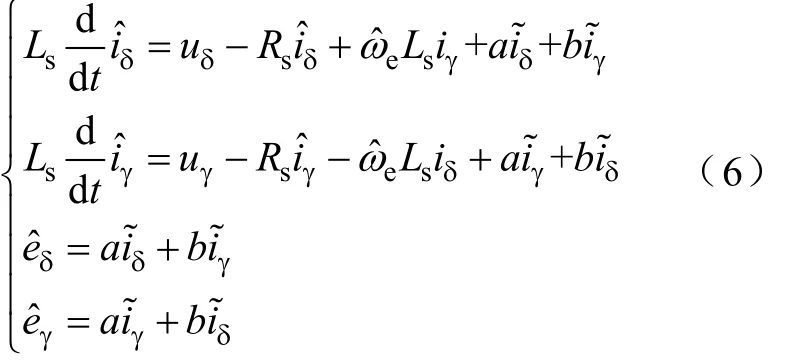
式中，——观测器输出；

，——观测误差，

a，b——反馈系数。

在得到反电动势分量后，利用反三角函数计算出角度误差Δθ为

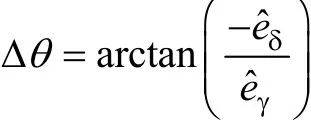
为了使估算得到的坐标与dq坐标系重合，即得到真实的动子位置，必须调节Δθ使其收敛于0，本文采用比例积分（PI）控制器来对Δθ进行控制，控制参考量为0。PI控制器的输出为估算得到的动子电角速度，通过对电角速度积分得到动子位置的估算值。该位置估算值被反馈给定子电压电流的坐标变换函数来更新估算的坐标位置信息。整个算法框图如图2所示。

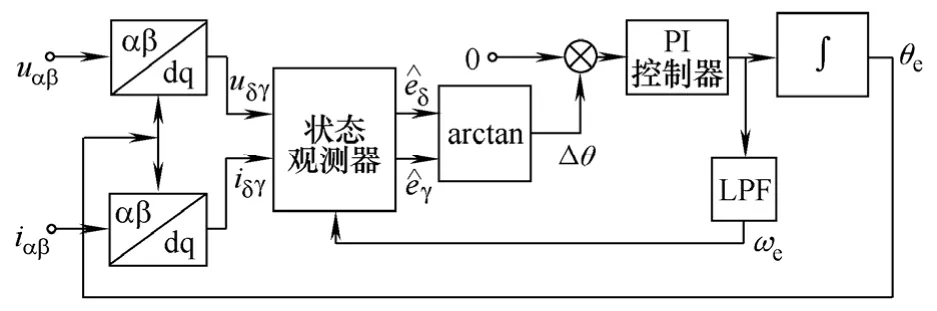
图2 速度和位置算法框图Fig.2 Speed and position estimation diagram

4 实验

4.1 实验平台

为了验证以上算法，利用基于 VME总线的控制系统和一台长定子同步直线电机搭建实验平台。

控制系统采用VMIC公司的VMIVME 7750工控计算机和VxWorks操作系统，动子磁场定向控制与位置和速度估算程序均在IOWorks环境中开发，IOWorks是VMIC公司提供的基于其公司硬件的编程环境，整套开发环境高度集成从而可以大大缩短开发周期。

实验电机为长定子直线同步电机，动子侧采用电励磁，电机参数如下：定子极距τ：258mm；定子电阻Rs：0.149Ω；定子电感Ls：1.92mH；动子励磁磁链φm：0.495Wb。

由以上参数可得电机动子的直线速度与电角速度之间关系为

实验中，电机的起步过程采用开环控制，当速度达到一定值后接入观测器的值构成闭环控制，整个系统的框图如图3所示。

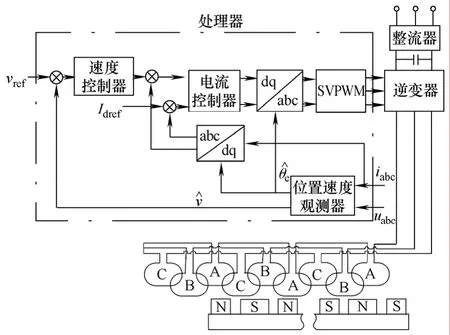
图3 实验系统框图Fig.3 Experimental system overview

4.2 实验结果

图4是电机正反向运动过程的速度曲线，速度正向给定最大值为3m/s，电角速度频率约为6Hz，反向最大为 1.5m/s，电角速度频率约为 3Hz。从图中可以看到速度估算效果良好，误差较小。同时也可以在图中注意到反向运行起动时刻速度估算误差有跳变，这是因为本算法不能估算零速时的电机位置，当起动时，位置估算值与实际值相差较大时估算值收敛到实际值的过渡过程会使速度估算产生较大误差。在起动时采用开环控制可以避免这一问题。

图5是电机在正向运行时的动子位置波形，包括实际位置和估算值。图6是图5的放大图，从图中可以看出位置估算效果良好，估算误差保持在0°附近。

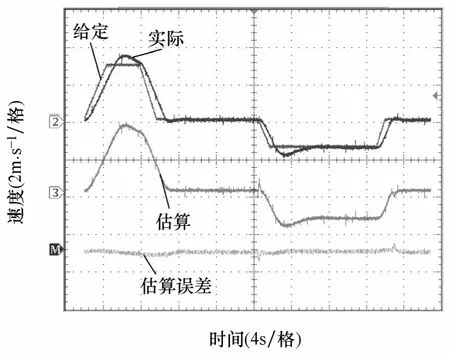
图4 电机运行的速度曲线Fig.4 Mover speed waveforms

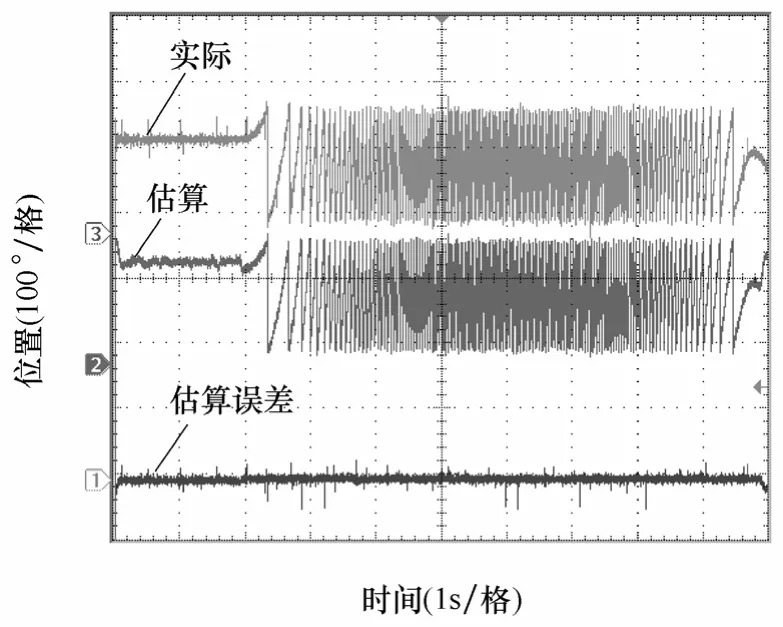
图5 电机正向运行期间的位置波形Fig.5 Mover position waveforms when moving in positive direction

5 结论

本文针对长定子直线同步电机的矢量控制提出了基于假设坐标系法的速度和位置估算方法，并通过电机试验平台验证。由实验结果可以看出，本文所采用的速度和位置观测方法能够实现对速度和位置很好的估算。

图6 位置波形放大图Fig.6 Detailed position waveform

[1] Plattner A. A millimetrewave communication system for maglev application[J]. Microwave Symposium Digest of IEEE MTT-S International, 1994, 2:745-748.

[2] Ng C H, Rashed M, Vas P, et al.A novel MRAS current-based sensorless vector controlled PMLSM drive for low speed operation[C]. Electric Machines and Drives Conference of IEEE International, 2003, 3:1889-1894.

[3] Wang Limei, Guo Qingding.Sensorless control of permanent magnet linear synchronous motor based on nonlinear observer[C]. The 8th IEEE International Workshop on Advanced Motion Control, 2004:619-622.

[4] Kim J H, Choi J W, Sul S K. High precision position control of linear permanent magnet synchronous motor for surface mount device placement system[C] .Proceedings of the Power Conversion Conference,2002, 1: 37-42.

[5] Leidhold R, Mutschler P. Speed sensorless control of a long-stator linear synchronous motor arranged in multiple segments[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3246-3254.

[6] Platen M, Henneberger G. Examination of leakage and end effects in a linear synchronous motor for vertical transportation by means of finite element computation[J]. IEEE Transactions on Magnetics,2001, 37(5): 3640-3643.

[7] Vas P. Electrical machines and drives: a space-vector theory approach[M]. New York: NY, USA: Oxford University Press, 1992.

[8] Mobarakeh B, Meibody Tabar F, Sargos F. A globally converging observer of mechanical variables for sensorless pmsm[C] . 2000 IEEE 31st Annual Power Electronics Specialists Conference, 2000, 2: 885-890.