新型UPQC直流电压的PIλDμ控制

梁祖权 束洪春

（1. 哈尔滨工业大学电气工程及其自动化学院 哈尔滨 150001 2. 昆明理工大学电力工程学院 昆明 650051）

1 引言

在实际控制系统中，非线性问题广泛存在，并且许多系统中的非线性元件越来越多，使得传统的控制问题也越来越多地开始采取非线性控制理论。目前，电力系统中的非线性元件也越来越多，且非线性问题广泛存在。由于许多实际系统本质上呈现分数而非整数阶次，如文献[1]分析得出电容对应的积分阶次是0.998次而不是通常的1次。在许多控制过程，如精确控制和非线性问题中，传统的控制很难完全适应非整数阶次的需要。

电力系统中，电能质量问题已经得到越来越多的重视，是目前研究的热点。统一电能质量调解器（UPQC）作为解决电能质量的有效设备，其有关的研究报道已很多，但如何使其工作在更优、更精确的状态以提高设备的控制效果仍需进一步研究。

分数微积分[2]是基本与古典微积分同时出现的数学，已经具有完整的理论，但其应用由于受到如数学处理工具等客观条件的限制而只在 20世纪后期才得到了发展。PID控制器作为控制系统的经典控制器，基本原理是通过基于整数阶次的比例、微分和积分控制器的组合和相应系数的调整来调节被控制系统，其控制灵活，实现简单，物理意义明确因而得到广泛的应用。目前PID控制的研究已经比较成熟，在此基础上出现了许多新型PID控制器，并在非线性特性方面也有文献报道[3]。目前 PIλDμ控制器[4]在电力系统控制中还没有报道。随着计算机技术处理器以及相应数学软件的高速发展，使其必将在电力系统及其他许多领域中得到新的广泛地应用。

2 分数阶基本定义

目前，分数微分方程的基本定义有许多，最广泛认可的有以下两种[2]：

Riemann-Liouville分数微分定义：

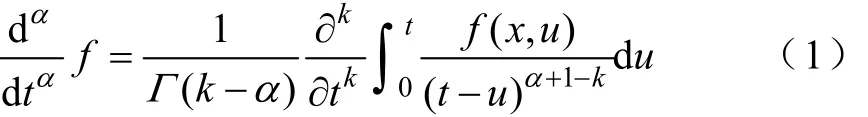
Caputo分数微分定义：

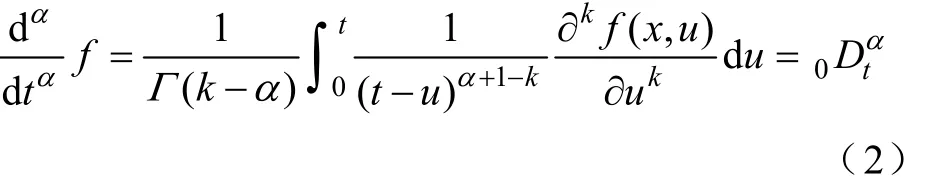
式中Γ(·)—— Gamma函数；

α—— 分数微积分的分数阶次，k为整数，k-1＜α≤k；

上述两种定义对于很多实际函数都是等效的，其区别在于对常数求导的定义不同，Caputo定义对常数的求导是有界的（为0），而Riemann-Liouville定义是无界的，Caputo定义更适用于分数阶微积分方程初值问题的描述。

2.1 分数阶 PIλDμ控制器

分数阶 PIλDμ控制器由 Podlubony提出并对其进行了研究[4]，国内学者[5]也对其进行了原理性的仿真研究，但尚未有其在电力方面应用的研究文献。其定义为

对上述Caputo定义进行Laplace变换后有

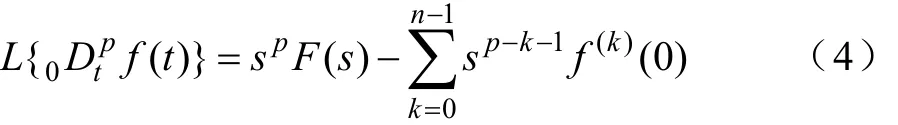
通过对0时刻的选取可以简化上式为

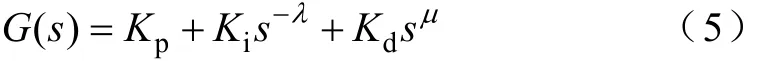
由式（5）可知

当λ=0且μ=0时，G(s)=Kp，为常规比例控制。

当λ=1且μ=0时，G(s)=Kp+Ki/s，为常规 PI控制器。

当λ=0且μ=1时，G(s)=Kp+Kds，为常规 PD控制器。

当λ=1且μ=1时，G(s)=Kp+Ki/s+Kds，为常规 PID控制器。

由于λ和μ可以为任意实数，所以经典的 PID控制实际上就是PIλDμ控制的特例，而PIλDμ控制可以看作为经典PID控制的拓展形式。通过选取不同的λ和μ值，能在很大程度上拓宽控制范围，有可能取得更好的控制效果。PIλDμ控制和经典PID控制最大不同在于：PIλDμ控制既可以调节三个增益系数Kp、Ki、Kd，同时还可以对积分和微分的阶次进行调节以增大或减少该环节的作用，故其结构更灵活，控制范围可以更广；另外，从分数微分的定义可知，其微分也具有记忆功能，故能确保历史信息对现在和未来的影响，从而有利于改善系统的控制品质；分数阶 PIλDμ控制器最突出的特点是具有更强的鲁棒性，其对控制参数的变化以及对被控对象系统参数的变化不敏感，只要参数在一定范围内变化，分数阶PIλDμ控制器都能很好地进行控制。

2.2 PIλDμ控制器存在问题

（1）由于PIλDμ控制器有5个自由度可以进行控制，故控制范围更广，但更多的阶次和系数的选取也增加了优化的难度。

（2）实际应用中还存在一定的困难，对于分数阶次的实现较复杂，在实际应用的不同情况要采取不同的形式来对待，例如对于离散系统来说由于纯粹的分数阶微分器是不能直接物理实现的，所以需要用FIR滤波器或IIR滤波器形式来近似，具体讨论将在后期工作中研究。

（3）PIλDμ控制器在实现上较复杂，在分数阶次的计算上要耗费较多的时间，如何提高计算时间和精度间的矛盾问题还有待研究。

3 UPQC直流电压控制系统

统一质量调解器（UPQC）[6]是用户电力的重要成员，能有效提高电力系统的电能质量，其具有消除谐波，补偿无功等功能。国内外有关的研究已经比较深入。为使主电路正常运行，需使UPQC直流侧电容电压维持在一固定的数值，以保证主电路在任何时刻都能跟随指令的变化产生正确的补偿量，否则会出现降低补偿精度的欠补偿和可能增加谐波的过补偿。直流侧电压变化的原因有：

（1）逆变器元件本身亦要消耗一定的能量而引起的电压变化。

（2）若系统中存在负序电流, 则其与系统电压在直流侧产生的能量脉动也可使直流电压波动；不同次的谐波电压和谐波电流的相互作用将与电容产生能量交换，从而使得直流侧电压发生波动等。

目前UPQC控制中通常采用的直流侧电容电压控制基本原理是：根据瞬时无功功率理论[6]，针对直流侧电容电压的实际测量值udc与基准值udcref之差，通过PI控制得到调节结果Ic，将其叠加到瞬时有功电流的直流分量上，补偿电流生成电路（UPQC并联部分）产生与其相应的补偿电流进入系统，使得UPQC的补偿电流中包含一定的基波有功电流分量，从而使UPQC的直流侧与交流侧产生能量交换，将udc调节到基准值。其原理如图1所示。

图1 直流电容电压控制原理Fig.1 The control scheme of the DC capacitor voltage

虽然UPQC的控制方法有许多，但直流电容电压控制的原理基本相同[7-8]，即通过 PI控制过程使得 UPQC补偿电流中包含一定的基波有功电流分量，其控制参数主要是比例和积分系数Kp、Ki，该过程中可能会有比较大的超调量和静差，响应速度也较慢。

对于直流电容电压的分数阶 PIλDμ控制器，只需将图 1中的 PI环节换成分数阶 PIλDμ控制器即可。

4 PIλDμ控制的实现

对于 PIλDμ控制器存在的问题，在具体实现时要有针对性的解决。文献[5]对 PIλDμ的控制主要是针对已知函数信号的处理，而在实际应用中控制信号通常是未知的或由于反馈等原因而很难精确表达的，因此对于该类信号需要采取如滤波器的形式来对其进行数值微分处理，即通过滤波器的输出来实现信号的分数阶数值微分运算。

文献[9]列出了许多连续滤波器的实现算法，本文亦采取其中的 Oustaloup算法来构造分数阶连续滤波器。假设拟合频率段为（ωb,ωh），其传递函数模型为

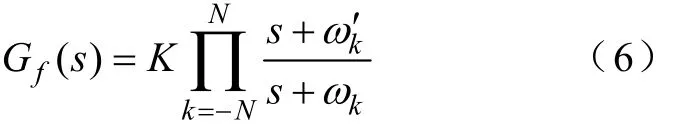
式中，滤波器的零极点、增益可由下式求出：

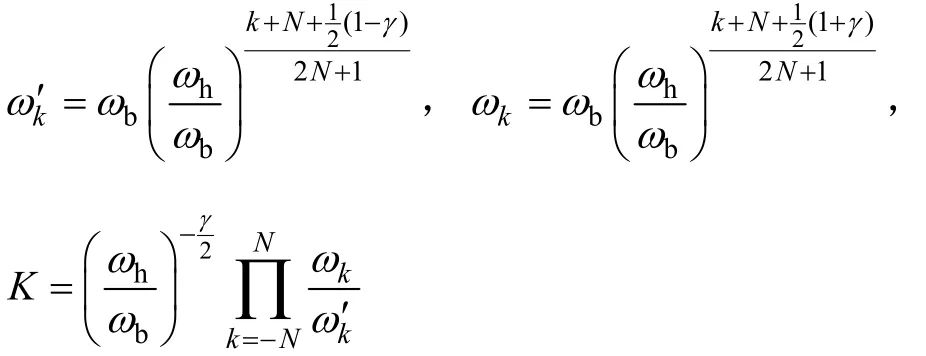
其中，r为分数阶次；2N+1为滤波器阶次；ωh、ωb是拟合频率的上限和下限，如果拟合的频率范围较大，需适当增加拟合的阶次。本文中ωb=0.0001，ωh=10000，N=4。

对于分数阶次的选取可以通过最优控制规则和主导极点法等方法来获得，考虑到直流电压控制本质上是一个优化过程，本文是就 PIλDμ控制器的效果进行评定，故对分数阶次的选取上以仿真结果为参考。

5 仿真及比较

Matlab是数学模型软件包，Matlab语言具有强大的计算功能和丰富的图形功能，编程效率高，扩充能力强，而且具有功能齐备的各种工具箱，所以Matlab语言已成为目前应用最广泛的数值计算软件，EMTDC/PSCAD是暂态分析程序，两者之间具有互补性，通过程序提供的接口可把两者的优点结合起来。本文采用 EMTDC/PSCAD来搭建 UPQC仿真模型。PIλDμ控制器采取上述的Oustaloup算法通过Matlab来实现，通过EMTDC/PSCAD与Matlab的接口来调用。

针对 UPQC直流电压的建立过程，采取 PIλDμ控制器，取Kp=0.55、Ki=10、Kd=0.001，利用 Matlab软件进行了仿真。

5.1 λ 对系统控制的影响

取λ值分别等于 0.85、0.95、1.0、1.005、1.01和1.2，得到直流电压的响应曲线如图2所示。由图2可知，随着λ的增大，直流电容电压的动态性能由差（λ=0.85）慢慢变好（λ=1.01），之后又变差（λ=1.2）。当λ＜1.01时，图 2中直流电压超调量的大小与λ的增加成反方向，λ越小，超调量越大；但当λ＞1.05后，动态响应效果又明显变差，主要表现在响应时间的增大上。

图2 不同λ 值下直流电容电压曲线Fig.2 The DC capacitor voltage waveforms of different values of λ

通过仿真结果对比后可以说明：通过改变λ的取值，能够有效地提高阶跃响应的控制效果，在非整数阶次积分环节下能够寻找到相比整数阶次积分环节具有更小超调量和响应时间的控制效果。

5.2 μ 对系统控制的影响

与分析λ时的条件相似，取Kp=0.55、Ki=10、Kd=0.001，并令λ=1。分别取μ值为 0.01、0.15、0.29、0.35、0.46和1.0，得到直流电容的电压波形如图3所示。

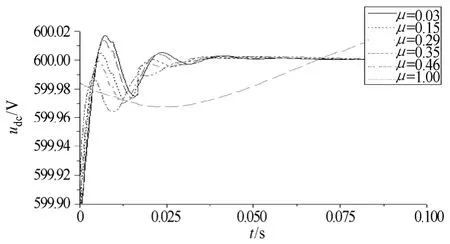
图3 不同μ 值下直流电容电压曲线Fig.3 The DC capacitor voltage waveforms of different values of μ

μ值的大小，意味着微分环节的强弱。由图 3可知，当μ=0.29时，直流电压的动态性能较好，而当μ值偏离0.29时（即大于或小于0.29时），直流电压的控制效果逐渐变差。

仿真结果同样说明：通过改变μ的取值，可以有效地提高阶跃响应的控制效果，在非整数阶次微分环节下能够寻找到相比整数阶次微分环节具有更小超调量和响应时间的控制效果。

5.3 UPQC直流电容电压PIλDμ控制的动态效果仿真

EMTDC/PSCAD与Matlab接口的内部结构如图4所示。

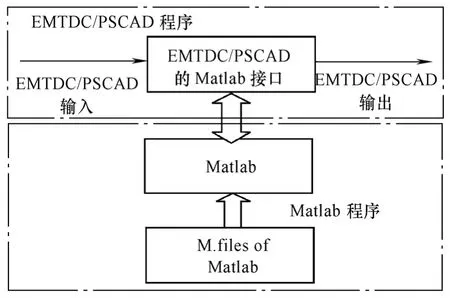
图4 EMTDC/PSCAD与Matlab接口示意图Fig.4 The scheme of EMTDC/PSCAD-Matlab interface

内部接口实现具体要求：

（1）在EMTDC/PSCAD中提供所定义的m文件。

（2）在利用EMTDC/PSCAD提供的自定义模块来实现与Matlab的接口，并对其输入和输出数据的类型和维数等性质进行定义，指定m文件的具体位置。

（3）需要采用Fortran90编译器并在EMTDC/PSCAD中设定F90编译器和Matlab的路径。

仿真中系统侧三相线电压为0.2kV，含有250Hz幅值为0.02kV和350Hz幅值为0.02kV的谐波电压，负载侧为三相整流电路接电阻 2.5Ω和电感 1mH的串联负载。UPQC在0.2s时投入，直流电容电压给定值为0.6kV。为考察其动态特性，在0.3s投入另一组负载，持续 0.06s后切除，仿真时间共 0.5s，利用上述方式求得的控制结果如图5和图6所示。图中的 3条曲线分别为采用传统 PI控制、PIλ控制和PIλDμ控制后的直流电容电压波形（图中符号udc之后的下标pi表示PI控制、fpi表示PIλ控制、fpid表示 PIλDμ控制）。其中，Kp=0.55、Ki=10、Kd=0.001；在 PIλ控制中，取λ=1.005；在 PIλDμ控制中，取λ=1.01，μ=0.3。

由上面的结果可知，在同样的Kp、Ki下，采取PIλ和 PIλDμ控制都能够更精确地得到控制结果，两者的差距不大，但传统的 PI控制则存在一定的误差，而由图6可知，分数阶控制器的动态效果也要好些，具有更小的超调量和响应速度，即 PIλDμ控制具有更强的鲁棒性和控制效果。对于本文所述的控制对象，由于 PIλDμ比 PIλ更难实现，所以采取 PIλ即可达到很好的控制效果。

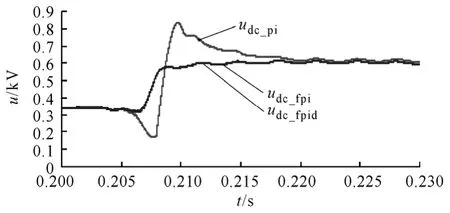
图5 直流电容电压放大波形Fig.5 The zooming in waveforms of the DC capacitor voltage

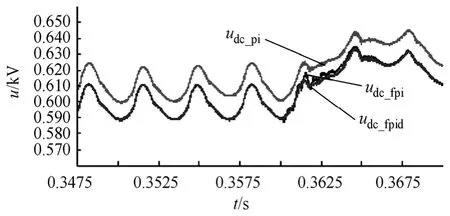
图6 直流电容电压局部放大波形Fig.6 The partly zoomed waveforms of the DC capacitor voltage

6 结论

分数阶 PIλDμ控制规律增加了控制器设计的灵活性，为进一步提高控制系统的性能提供了可能。本文设计了 PIλDμ控制器，并将其应用于 UPQC直流电容电压的定值控制。仿真结果显示，PIλDμ控制较传统的 PI控制，要更加精确且具有更强的鲁棒性，结构更灵活，控制范围也更广，可以应用于精确控制和非线性问题。

[1] Westerlund S. Capacitor theory[J]. IEEE Trans. on Dielectrics Electron Insulation, 1994, 1(5): 826-839.

[2] Podlubny I. Fractional differential equations[M]. New York: Academic Press, 1999.

[3] 胡包钢. 非线性PID控制器研究—比例分量的非线性方法[J]. 自动化学报, 2006, 32(2): 219-227.

Hu Baogang. A study on nonlinear PID controllersproportional component approach[J]. Acta Automatica Sinica, 2006, 32(2): 219-227.

[4] Podluby I. Fractional-order systems and PIλDμ-controllers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-214.

[5] 曾庆山, 曹广益, 王振斌. 分数阶 PIλDμ控制器的仿真研究[J]. 系统仿真学报, 2004, 16(3): 465-473.

Zeng Qingshan, Cao Guangyi, Wang Zhenbin.Simulation research on fractiona1 order PIλDμcontroller[J]. Journal of System Simulation, 2004,16(3): 465-473.

[6] Fujita H, Akagi H. The unified power quality conditioner: the integration of series and shunt-active filters[J]. IEEE Transactions on Power Electronics,1998, 13(2): 315-322.

[7] 朱鹏程, 李勋, 康勇, 等. 统一电能质量控制器控制策略研究[J]. 中国电机工程学报, 2004, 24(8):67-73.

Zhu Pengcheng, Li Xun, Kang Yong, et al. Study of control strategy for a unified power quality conditioner[J]. Proceedings of the CSEE, 2004, 24(8):67-73.

[8] 李鹏, 杨以涵. 基于H∞控制理论的UPQC串并联单元协调控制的实现[J]. 中国电机工程学报, 2006,26(20): 91-97.

Li Peng, Yang Yihan. Realization for coordinated control of UPQC series unit and shunt unit based onH∞control theory[J]. Proceedings of the CSEE, 2006,26(20): 91-97.

[9] 张邦楚, 王少锋, 韩子鹏, 等. 飞航导弹分数阶PID控制及其数字实现[J]. 宇航学报, 2005, 26(5):653-656.

Zhang Bangchu, Wang Shaofeng, Han Zipeng, et al.Using fractional-order PID controller for control of aerodynamic missile[J]. Journal of Astronautics，2005,26(5): 653-656.

[10] Axtell M, Bise E M. Fractional calculus application sin control systems[C]. Proceedings of the IEEE 1990 Nat. Aerospace and Electronics Conf, New York,USA, 1990: 563-566.

[11] 楼森岳, 唐晓艳. 非线性数学物理方法[M]. 北京：科学出版社, 2006.

[12] 袁晓, 张红雨, 虞厥邦. 分数导数与数字微分器设计[J]. 电子学报, 2004, 32(10): 1658-1165.

Yuan Xiao, Zhang Hongyu, Yu Juebang. Fractionalorder derivative and design of fractional digital diferentiators[J]. Acta Electronica Sinica, 2004,32(10): 1658-1165.

[13] 蔡智富, 张雯雯, 刘志宏, 等. 基于提升静态小波-分数阶傅立叶变换的 LFM 识别[J]. 数据采集与处理, 2008, 23(5): 542-546.

Cai Zhifu, Zhang Wenwen, Liu Zhihong, et al.Recognition of LFM signals based on lifting SWT-FRFT[J]. Journal of Data Acquisition &Processing, 2008, 23(5): 542-546.

[14] Xue Dingyu, Chen Yangquan. Fractional order calculus and its applications in mechatronics and power electronics-an introduction[C]. 2nd IEEE Conference on Industrial Electronics and Applications, 2007: xlvi.