SF6断路器开断并联电抗器的截流过电压及其特性分析

孙秋芹 李庆民 王 冠 刘洪顺 邹振宇

（1. 山东大学电气工程学院 济南 250061 2. 山东电力工程咨询院 济南 250100）

1 引言

并联电抗器广泛安装于超、特高压等级的输电线路中，它能够补偿线路的对地充电功率，削弱输电线路的电容效应，有效抑制工频与操作过电压。

目前超/特高压电压等级的断路器多采用外能方式灭弧，利用这种断路器分断电流时，弧道中游离作用并不强烈，随着电弧的急剧拉伸，弧阻增加，易发生电弧不稳定现象，电流在到达零点之前可能发生强制熄弧，形成截流，产生严重的操作过电压[1-6]。电抗器正常运行时储存一定的能量，一旦被切除，该能量将通过电抗器的等值入口电容释放，因该电容值很小，故会激发出很高的过电压，2002年我国新疆电网在开断并联电抗器时曾发生过相应的爆炸事件[1]。

国内外学者对开断并联电抗器过电压进行了大量研究。文献[2]通过引入断路器触头的分离速度，建立相应的介质绝缘强度函数，给出了顺利开断并联电抗器以及电弧重燃时负载侧和电源侧的过电压波形。文献[4]通过引入断路器电弧模型及其介质绝缘强度函数，对并联电抗器的开断特性进行了分析。文献[5]给出了并联电抗器的详细模型，重点分析了开断并联电抗器时线圈匝间的过电压情况，并与试验波形相对比，取得了较好的效果。此外，其他学者也开展了一些相关方面的研究[6-8]。上述研究主要集中在并联电抗器中性点直接接地或不接地的情况， 而对并联电抗器中性点经小电抗接地关注较少。同时以往研究主要针对并联电抗器在安装现场的开断情况， 而带长线开断并联电抗器（切带并联电抗器的空载线路）也是一种有效的方法，值得关注。随着超/特高压输电线路的迅速发展，中性点接小电抗以熄灭潜供电弧的补偿方式将占据主导地位，必须给予重视。

本文首先分析了带中性点小电抗的并联电抗器的开断过程和过电压情况，阐明了断路器开断后拍频振荡产生的机理，并计算出不同工况下的拍频振荡频率。结合某 750kV线路， 使用 ATP-EMTP软件，通过引入较精确的 SF6断路器电弧模型，详细研究了并联电抗器开断过程中的电磁暂态特性，并将仿真与理论分析进行了比较。

2 开断并联电抗器过电压

2.1 过电压分析

开断并联电抗器时，其单相等效电路如图1所示。图中Us为等效电源电压，Ls为电源侧等效电感，Cs为电源侧等效电容，L为并联电抗器电感，CL为并联电抗器侧对地电容，Lp和Cp为断路器等效电感和电容。

设t=t0时断路器触头分开，断路器的截流值为Ich，此时电容CL上的电压为U0；当回路总磁场能全部转化为电场能时，电容CL上的电压最大为Um，且满足

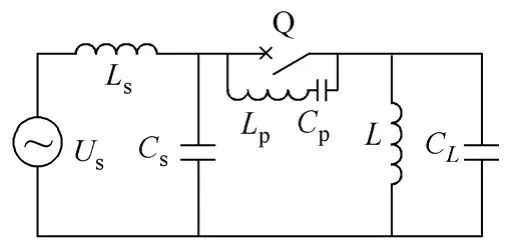
图1 开断并联电抗器的单相等效电路Fig.1 Single-phase equivalent circuit for shunt reactor interrupting

以U0为基准电压，开断并联电抗器时产生的最大过电压倍数K为

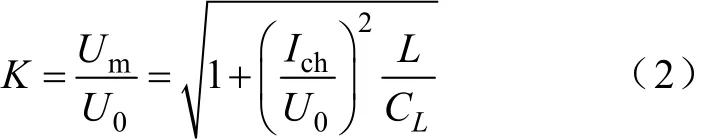
实际中对于带铁心的电抗器，由于铁心及其铜线损耗，在磁能与电能的转化过程中，部分磁能将会损失掉，为此可引入转化磁能系数ηm，则式（2）变为

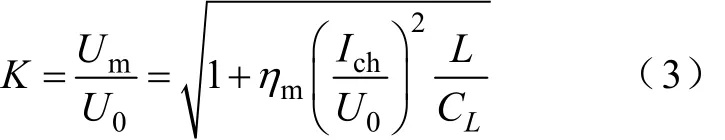
开断时的过电压倍数与并联电抗器的种类、额定电压、容量、结构以及断路器的种类有关。当变电站近距离开断并联电抗器时，由于并联电抗器的入口电容很小，其最大过电压倍数很大，通常会超过电气设备的绝缘水平。

并联电抗器中性点带小电抗时，由于断路器动作时间不同期，三相开断和截流时刻并不一致。首相高抗先被开断后，中性点电压将产生偏移而升高，此时的等效电路如图2所示，电抗器线路侧单相电压有效值为Uφ，电抗器高压臂的值为L，小电抗器的值为LN。

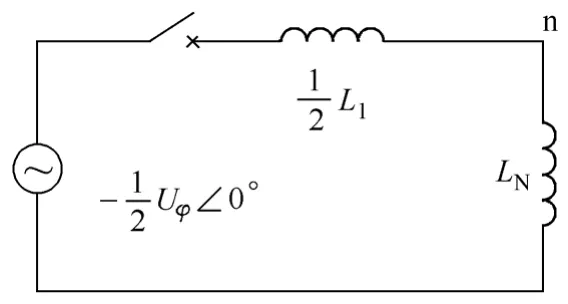
图2 首相开断后的等效电路Fig.2 Equivalent circuit after the first phase opening

则中性点n处的电压Un为

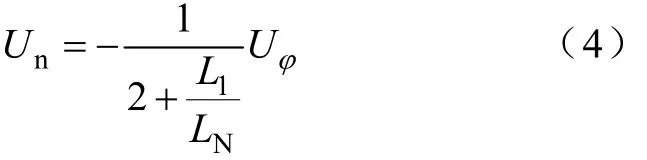
式中

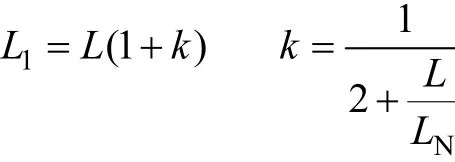
被开断相电压计算电路如图 3所示，其中CL为电抗器对地电容。

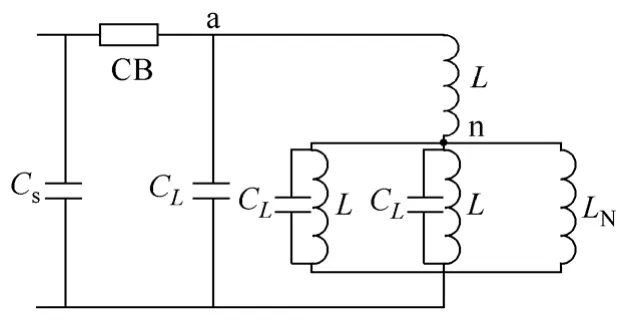
图3 单相开断后过电压计算电路Fig.3 Overvoltage calculation circuit after single-phase interrupting

设U0为首开相被开断后瞬间的对地电压值，由于中性点电压偏移，则图3中对应的a点电压升高为（1＋k）U0。由电磁能量平衡，可知首开相的电压方程为

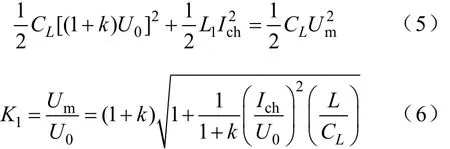
考虑ηm后，式（6）变为

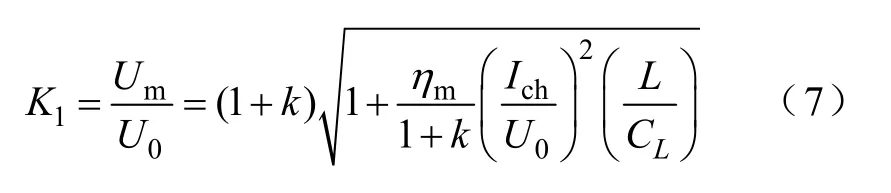
式中，Um为被开断相出现的电压峰值；K1为过电压倍数。在一定参数范围内，令ηm=1时（空心电抗器ηm≈1），过电压倍数随高抗和小电抗变化的轨迹如图4所示。

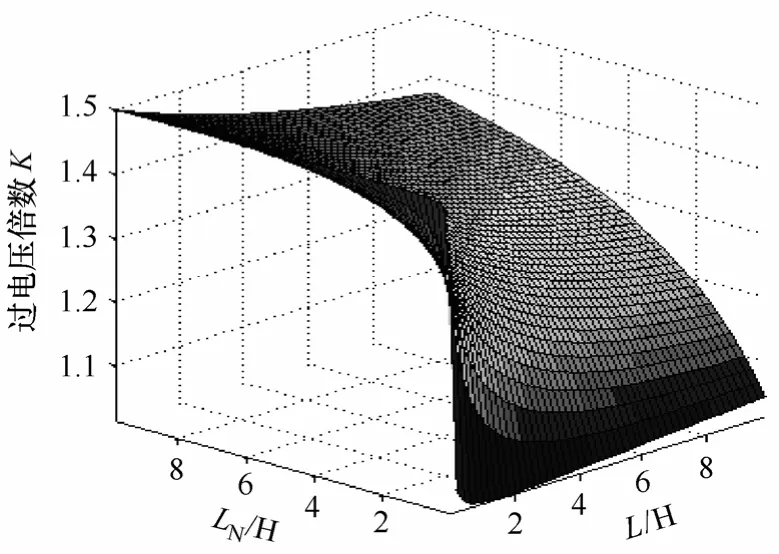
图4 不同电抗器参数下的过电压倍数Fig.4 Scenario of the overvoltage vs.parameter variation

由图4可以看出，在一定参数范围内，首相开断后的最大过电压倍数随中性点小电抗的增大而增加。当带长线开断并联电抗器时，并联电抗器与线路电容构成振荡回路，CL大大增加，则对应的过电压倍数将会减小。

2.2 过电压频率特性分析

断路器三相分闸开断并联电抗器后，并联电抗器侧构成一个孤立的系统，因并联电抗器的电感和对地电容中储存了大量能量，形成电磁能量转换的振荡回路。分析开断电抗器时过电压的振荡频率特性，可为研究断路器的恢复电压与重燃、线路的匝间纵向绝缘、电抗器参数的集肤效应等提供参考依据。

文献[6]中忽略相间电容耦合，给出了简化的计算公式。当近距离开断并联电抗器时，公式可近似成立；但当带长线开断并联电抗器时，相间耦合则不能忽略。并联电抗器开断后三相电感间通过电容耦合形成充放电回路， 其简化原理图如图5所示。

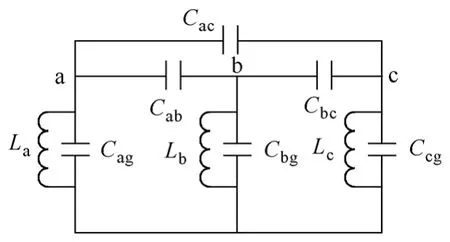
图5 三相并联电抗器的电磁耦合Fig.5 Electromagnetic coupling circuit of the shunt reactor

图5中La、Lb、Lc为三相并联电抗器等效电感，Cag、Cbg、Ccg为三相对地电容，Cab、Cbc、Cac为相间耦合电容。若令Cab=Cbc=Cac=CΔ，La=Lb=Lc=L，Cag=Cbg=Ccg=C，通过求解回路方程，可推出电路中两个主要自振频率的计算公式为

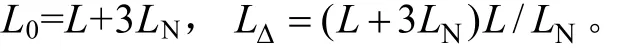
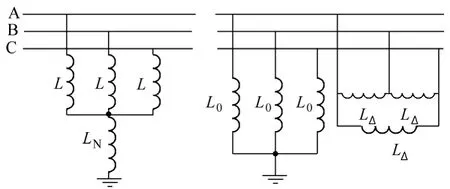
图6 并联电抗器加小电抗的等效变换Fig.6 Equivalent circuit transformation of the four legged reactor

解回路方程得，并联电抗器开断后，电路中将存在两个主要的自振频率，其计算公式为

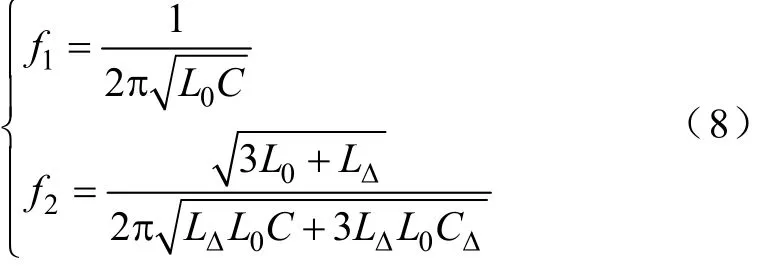
则此时电压的拍频振荡频率f为

计算表明，接中性点小电抗的并联电抗器组开断后，其过电压的振荡频率低于对应条件下不接中性点小电抗的情形。

参照文献[3～5]中的数据，令C＝15.62nF，CΔ=0.236nF，在变电站近距离切并联电抗器时，过电压的拍频振荡频率随高抗和小电抗变化的曲线如图7所示。

当带长线路开断并联电抗器时，令C=1.18μF，CΔ=0.107μF，则对应的拍频频率随高抗和小电抗变化的曲线如图8所示。此时因CΔ和C大大增加，对应的电路自振荡频率均大大减小，导致拍频振荡频率减小。

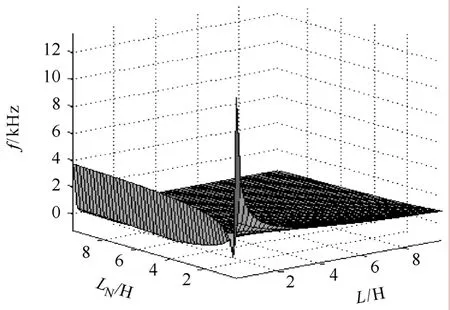
图7 近距离开断并联电抗器时的拍频频率Fig.7 Beat frequency of the oscillating overvoltage while the shunt reactor is interrupted at a short line distance

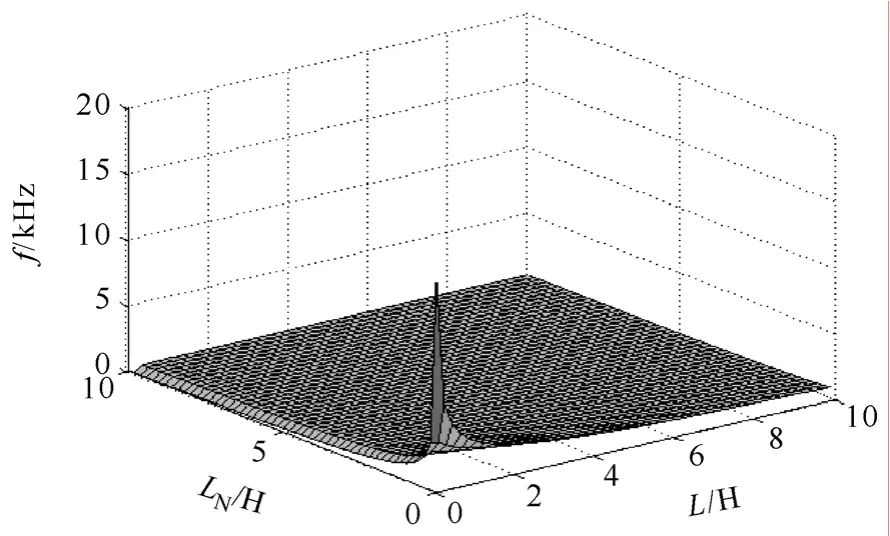
图8 带长线开断并联电抗器时的拍频频率Fig.8 Beat frequency of the oscillatory overvoltage while the shunt reactor is interrupted with a long transmission line

带长线开断并联电抗器时，拍频频率随着LN和L的增大而增大，但近距离切并联电抗器时，情况则较为复杂。由于CΔ和C的值较小，同时考虑到铁心元件中必然存在磁滞、涡流等损耗，电抗器侧的实际过电压多呈衰减的拍频振荡波形。

3 仿真研究

3.1 计算对象

基于某750kV输电线路构建了仿真模型，采用ATP-EMTP软件，在输电线路空载时计算得到了并联电抗器开断前后的过电压情形。线路结构如图 9所示。其中，S和 R表示输电线路的首、末端；N为并联电抗器的中性点，并联电抗器高抗的补偿度为90%。Q1和Q2为SF6断路器，r和rN为电抗器高压臂和小电抗的等效电阻值。电路正序参数为：R1=0.0133Ω/km，L1=0.347mH/km，C1=0.0138μF/km；零序参数为：R0＝0.3216Ω/km；L0＝2.65mH/km；C0＝0.0098μF/km。

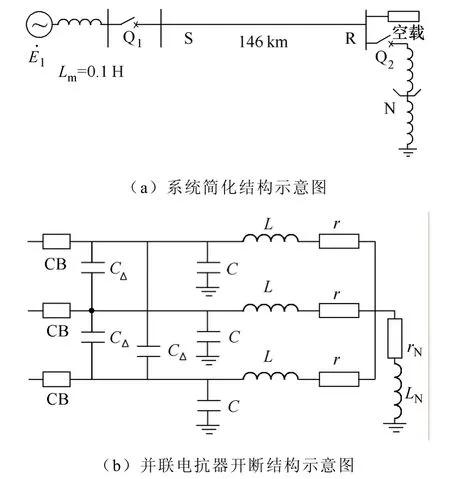
图9 750kV输电系统仿真图Fig.9 Simulation model of the 750kV transmission system

开断过程中电抗器侧产生的过电压频率很高，特别是在近距离开断电抗器时，导线和电抗器的电阻会因强烈的集肤效应而增大。当前考虑频变效应的处理方法主要有两种：①仿真时采用考虑频变的J. Marti线路模型；②通过预先的简化计算，先获得过电压的大致振荡频率，然后直接计算该频率下导线和电抗器的相关参数。第一种方法的处理结果相对准确，但需要的计算步长较小，耗时较多；第二种方法较为简便，一般情况下也能满足计算精度要求[5]。本文采用第二种方法进行计算，近距离开断时，参数计算频率为500Hz；带长线开断时，采用工频频率。

3.2 断路器电弧模型

断路器电弧是一个复杂的物理、化学过程。对一些难以实现或实现起来代价太大的开断实验，通过引入电弧模型进行计算，并使开断过程的仿真更符合实际情况，其有效性在一些相关试验中得到了验证[2-5,7-8]。最早的电弧模型是Cassie模型和Mayr模型，其中Cassie模型主要适用于电流过零前的大电流阶段，Mayr模型主要适用于零区小电流阶段。以这两种模型为基础，针对其固有不足，很多人对电弧模型进行了改进[10-14]，陆续提出的电弧模型主要有：Habedank电弧模型、KEMA电弧模型、改进的Mayr模型、Schavemaker电弧模型、Kopplin模型、Urbanek模型等[11]。各种电弧模型的适用范围不同，本文在仿真中采用应用较为广泛的 Schwarz电弧模型，其中电弧散热功率和时间常数为电弧电导的函数，具体表达式为[11]

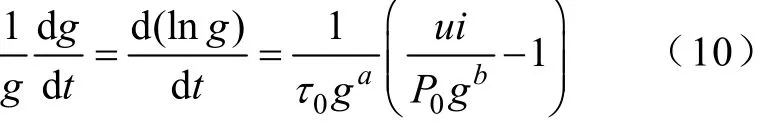
式中，u、i、g、P0、τ0分别为电弧电压、电弧电流、电弧电导、散热功率以及散热时间常数。参照文献中的数据[3-5,11-12]，取P0＝108W，τ0=6μs，a=0.15，b=1.8。

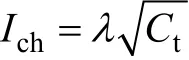
3.3 仿真结果

为开断线路末端R处的并联电抗器，采用两种仿真方案，如图9所示：①变电站近距离开断，即打开断路器Q2，直接开断线路末端的并联电抗器；②带长线开断并联电抗器，即先打开 Q1，再打开Q2开断末端的并联电抗器。设断路器在 0.1s时动作，两种方案下的仿真波形如图10～图14所示。

表 不同 λ 下的过电压幅值Tab. Peak overvoltages under different λ

由上表可知，随着λ的增大，截流值增大，电抗器侧的过电压幅值快速上升。

当λ=10×104时（图10～图14均采用此条件），同一截流水平下，分别采用理想开关和电弧模型，在近距离开断电抗器时，得到电抗器侧的过电压波形如图10所示。

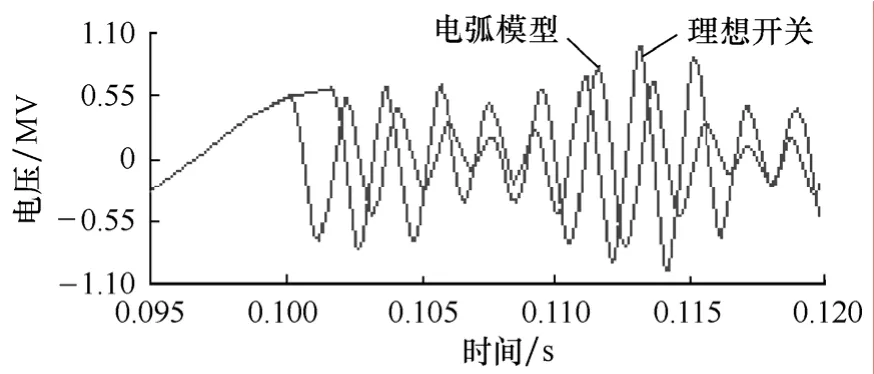
图10 电弧模型和理想开关下电抗器侧的过电压Fig.10 Overvoltages along the shunt reactor under arc model and ideal switch

由图10可知，两种模型下的过电压仿真波形存在较大差别，实际的开关电弧相当于一个非线性电阻，它将吸收一部分能量，使得过电压的幅值减小，引入电弧模型能更真实地反应实际的开断过程。

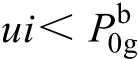
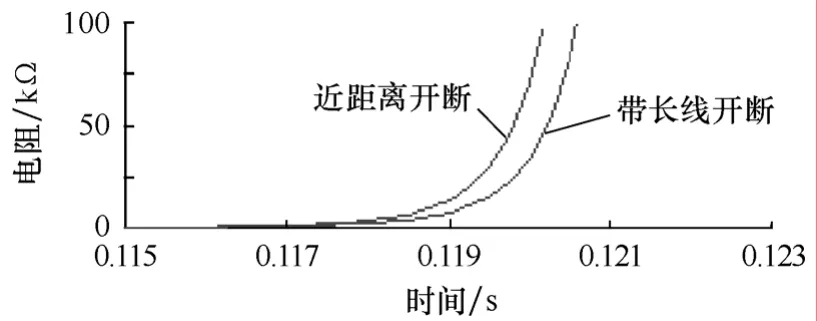
图11 电弧电阻Fig.11 Arc resistance

图12给出了开断并联电抗器时，其高压臂的过电压波形（图 12～图 14均将电弧特性考虑在内）。

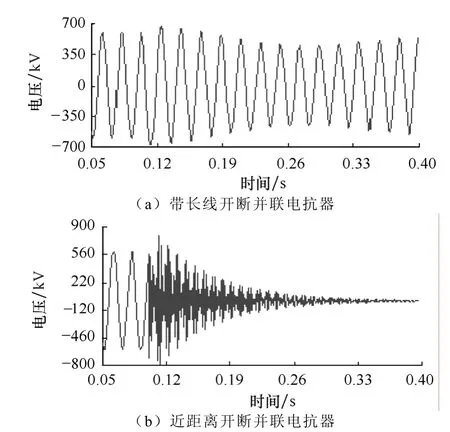
图12 线路末端电压Fig.12 Overvoltages at line terminal

由图12可知，两种方案切并联电抗器时，都会产生明显的拍频振荡现象。带长线切时，电抗器通过输电线路释放一部分能量，电抗器侧的过电压较低，拍频频率也较小，但电压的衰减速度较慢。近距离切并联电抗器时，因对地电容小，过电压幅值较大，拍频频率较高，同时电压衰减也较快。

对近距离切时的线路末端电压（如图12b所示）进行傅里叶分析可知，电压振荡的两个主要频率分别为 520Hz和 420Hz，则对应的拍频振荡频率为100Hz。采用式（6）与式（7）进行计算，得到的振荡频率分别为528Hz和425Hz，则拍频振荡频率为103Hz。仿真结果与理论分析结果非常接近。

在并联电抗器开断过程中，并联电抗器中性点的电压变化波形如图13所示。

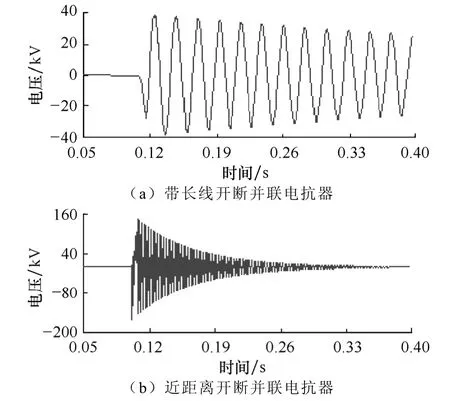
图13 末端并联电抗器的中性点电压Fig.13 Neutral point voltage of the shunt reactor at line terminal

由图13可知，相同条件下，带长线开断时，对应的电抗器中性点电压要远小于近距离开断的情况。近距离开断时，需考虑在中性点安装适当避雷器以抑制过电压。

并联电抗器开断后，断路器触头间的恢复电压波形如图14所示。

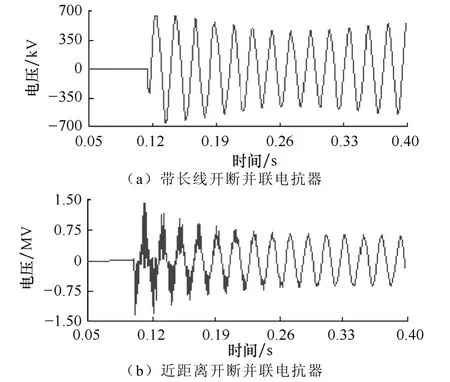
图14 断路器的瞬态恢复电压Fig.14 Transient recovery voltage of the circuit breaker

断路器触头间的恢复电压波形表现为不同的瞬态特性。当带长线开断并联电抗器时，瞬态恢复电压波呈拍频振荡，衰减较慢，触头间恢复电压及其上升率较小，对应的断路器重燃概率小；当近距离开断时，触头间恢复电压及其上升率很大，衰减也快，很快变为稳定的正弦波，但断路器重燃概率大，时易产生较大的重燃过电压。

4 结论

通过建立等效电路模型，从理论上分析了带长线和近距离开断并联电抗器时的过电压及其频率特性。基于实际的750kV输电线路参数，通过引入SF6断路器的开关电弧模型，进行了仿真计算和比较。

（1）并联电抗器开断时易产生截流，形成的过电压幅值主要取决于截断电流水平。随着截断电流的增加，过电压呈非线性增长。

（2）并联电抗器开断时，会产生拍频式振荡电压，其特性影响断路器的恢复电压与重燃、线路的匝间纵向绝缘、电抗器的参数等，拍频振荡频率与线路的电容密切相关。

（3）带长线开断并联电抗器是一种有效抑制开断过电压的方法，电抗器通过输电线路放电而释放能量，能减小并联电抗器侧的过电压。因相对地电容较大，振荡频率相对较小，电压衰减较慢。

（4）近距离开断并联电抗器时，其中性点可能会产生幅值很高的过电压，需考虑在小电抗附近安装避雷器。与此同时，断路器触头间的瞬态恢复电压及其上升率很高，易引起断路器的重燃。可考虑采用相控断路器以减小重燃率，或考虑安装并联开断电阻，以减小并联电抗器开断时的过电压。

（5）比较理想的补偿措施是研制智能化的连续可控电抗器，以适应不同类型的线路和运行工况，减小断路器开断并联电抗器的操作，但在超/特高压等级获得实用尚有待于技术进步。

[1] 平绍勋. 电力系统内部过电压保护及实例分析[M].北京: 中国电力出版社, 2006.

[2] Vahidi B, Ghatrehsamani A, Kashi S A. Shunt reactor switching simulation by EMTP[C]. IEEE Melecon,2004: 939-941.

[3] Peelo D F, Ruoss E M. A new IEEE application guide for shunt reactor switching[J]. IEEE Transaction on Power Delivery, 1996, 11(2): 881-887.

[4] Gary W Chang, Hunter M Huang. Modeling SF6circuit breaker for characterizing shunt reactor switching transients[J]. IEEE Transaction on Power Delivery, 2007, 11(3): 1533-1540.

[5] Prikler L, Ban G, Banfai G. EMTP models for simulation of shunt reactor switching transients[J]. Electrical Power and Energy Systems, 1997, 19(4): 235-240.

[6] 杨大卫. SF6断路器切并联电抗器组实验研究[J]. 高电压技术, 1992, 64(2): 50-55.

Yang Dawei. Test and research on disconnecting shunt reactors with SF6circuit breakers[J]. High Voltage Engineering, 1992, 64(2): 50-55.

[7] Ching Yinlee, Chang Jhih, Chen Chao Rong, et al.Comparison of transient phenomena when switching shunt reactors on the line’s two terminals and station busbar[C]. International Conference on Power Sysem,PEWERCON Singapore, 2004: 1255-1260.

[8] Peelo D F, Avent B L, Darkos J E. Shunt reactor switching tests in BC Hydao’s 500kV systems[J].IEEE Proceeding of Generation and Transmission,1988, 135(5): 400-435.

[9] Application guide for shunt reactor switching[S].IEEE Standard C37.015, Dec, 1993.

[10] 黄绍平, 杨青, 李靖. 基于Matlab的电弧模型仿真[J].电力系统及其自动化学报, 2005, 17(10): 64-66.

Huang Shaoping, Yang Qing, Li Jing. Simulation of arc model based on Matlab[J]. Proceedings of the CSU-EPSA, 2005, 17(10): 64-66.

[11] Schavemaker P H. Arc model blockset[DB]. Power Systems Laboratory, Delft University of Technology,the Netherlands (eps.et.tudelft.nl), 2001.

[12] Schavemaker P H, Van der Sluis. An improved mayr-type arc model based on current-zero measurements[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 580-584.

[13] Phaniraj V, Phadke A G. Modeling of circuit breakers in the electromagnetic transients program[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 799-805.

[14] Landry M, Jean G, Jean R, et al. Dielectric withstand and breaking capacity of SF6circuit breaker at low temperatures[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1029-1035.