基于正则形理论的非线性稳定因子

邓集祥 姜 涛 姜传霏 欧小高

（东北电力大学电气工程学院 吉林 132012）

1 引言

由于得不到非线性动态电力系统解析解，所以电力系统大扰动下的稳定分析无法使用特征分析方法，主要都是利用数值方法求解。近年来，由于有了电力系统二阶近似解[1-6]，所以用解析法分析电力系统的动态特性，也就是在模态空间分析电力系统的动态特性就有了可能。大区电网的互联，系统stressed度增强，系统非线性对系统稳定的影响加大的情况下，即使一个在以往研究中不被重视的较小的扰动，由于系统非线性的加大也可能不允许再被忽略。这时，动态电力系统的二阶近似解[1-6]就起到了从另一侧面更有效地分析系统稳定与动态特性的作用。但组成二阶近似解的主要成分仍然是线性化分析中的eλi，即基本元素仍然是模式λi[3-8]，所以只要Re(λi.)＜0，通过近似解分析的结果系统就将是稳定的。即使这时的扰动已大到足以使系统失稳，或者扰动持续的时间也长到足以使系统失稳，由这些解或这些解曲线也得不到或看不出系统失稳的情况。

本文在研究正则形二阶变换[7,9]过程中省略的交叉项和三阶项的基础上，提出了分析大扰动下电力系统稳定的阻尼因子和稳定域因子的新概念，从而得到解决上述问题的一个新方法。在形成这两个因子的过程中不仅考虑了每个模式的高阶项，而且进一步考虑了模式间的非线性相关作用。阻尼因子是用来描述随着扰动持续时间的不同，每个正则形变量幅值变化快慢的情况；稳定域因子被用来确定每个正则形变量在不同的扰动持续时间下的大致稳定范围。即通过阻尼因子和稳定域因子可以分析大扰动下电力系统非线性振荡曲线特征的改变情况，获得振荡曲线幅值和周期发生变化的一些重要信息，进而从解析解这一侧面来研究大扰动下电力系统的稳定性。对小扰动下的 stressed系统，通常的特征分析方法无法适应其强非线性时，本文提出的方法同样适用。算例结果证明了本文所提出的非线性稳定因子这一新概念的正确性和在电力系统中应用的有效性。

2 二阶正则形变换

动态电力系统可以描述为

式中，X为状态变量；X0为f(X)的平衡点。

对式（1）泰勒级数展开如下：

式中，A为系统一阶部分的系数矩阵，即系统的雅可比矩阵。通过以下的线性变换：

式中，U为A的右特征矢量阵，系统（1）可以转化为以下形式：

式中，JY代表线性部分；F2(Y)代表F(Y)泰勒级数展开式二阶项；F3(Y)代表F(Y)泰勒级数展开式三阶项，H.O.T为F(Y)泰勒级数展开式四阶和四阶以上项。

对式（4）中的二阶项F2(Y)进行坐标变换：

在Z非常小的情况下，有

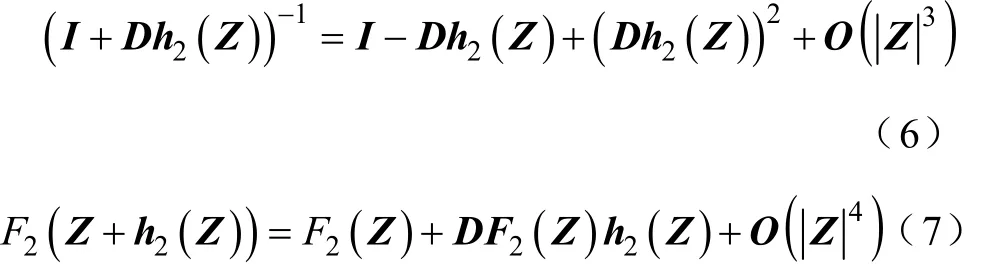
式中，I为N×N单位阵；Dh2(Z)和DF2(Z)分别为h2(Z)和F2(Z)的雅可比矩阵。

把式（5）代入式（4）并应用式（6）和式（7）得

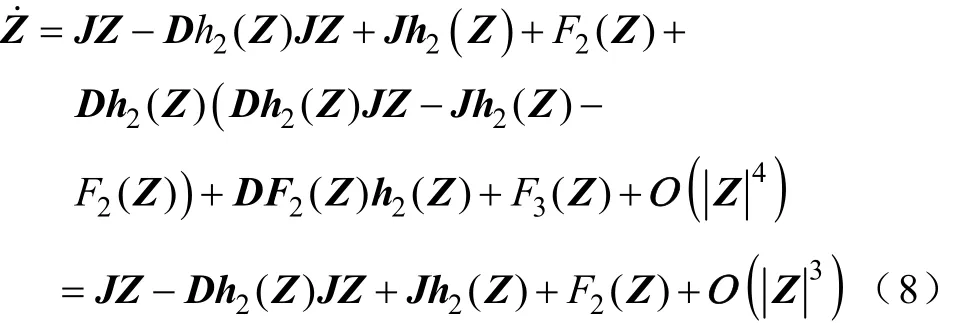
为了消去式（7）中的二阶项，变换式（4）必须满足方程

式中，Fl为F的第l个元素；λl为A的第l个特征值。

在式（5）的条件下，系统（4）可以转化为

如果令系统第i个模式λi=σi+jΩi，在只考虑振荡模式的情况下简化式（12），可得

式中，为zj的共轭。去掉式（13）右端高阶项就是通常二阶正则形矢量场[6]，而式（13）中的zi则是考虑了二阶变换中省略的交叉项和三阶项后新的正则形变量。

根据二阶变换式（9）和式（10）可以得到

设式（15）中的实部为aij，虚部为bij，则有

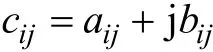
3 正则形二阶变换所省略三阶项的坐标变换

式中，ri代表模式i的幅值；θi代表模式i的相角。

在仅仅考虑模式i的情况下，式（16）和式（17）可写为

根据式（18）可得

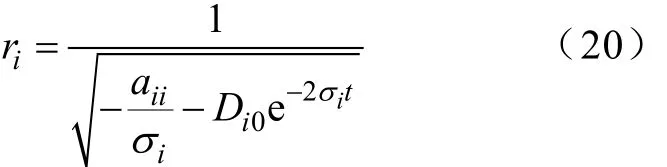
将式（20）代入式（18）整理得

4 非线性稳定因子的分析

4.1 阻尼因子aij

由于aij代表了二阶正则变化中省略的三阶交叉项的系数，所以描述了模式i和模式j之间的非线性相互作用。进而，由于式（14）的第二项和式（15）的相互作用形成对正则形变量zi的影响可以直接通过aij的计算来定量估计。

4.2 稳定域因子Ri

如果式（16）中aiM(M≠i)与aii相比较小，即除模式i以外其他模式间相互作用很弱（也就是模式i不与其他模式发生一阶谐振和一阶准谐振[6]）时，正则形变量zi的幅值为

式中，Ri给出了正则形变量zi的大致稳定范围，当ri＞Ri时（正则形变量zi的幅值超过Ri），由式（18）知ir˙＞0。显然，这时系统将失稳。即使特征分析指出系统在平衡点是稳定的，也就是说，即使所有模式的实部都小于零，系统振荡也将是发散的。

5 算例分析

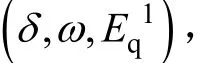
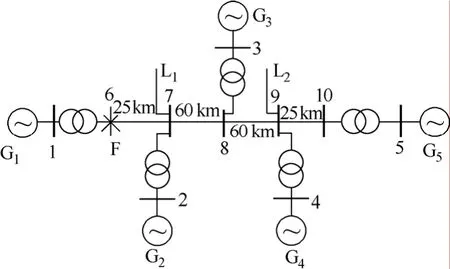
图1 五机系统Fig.1 Five-generator system

表1 低频振荡模式Tab.1 Inertial modes

表2 非线性稳定因子Tab.2 Nonlinear stability factor

为验证上述计算分析的正确性，针对这些不同的故障清除时间进行时域仿真，结果如图 2～图 7所示。其中图2、图4和图6是依据式（20）所得的z1和z2振荡曲线，图3、图 5和图7是发电机G2、G3、G4转子角曲线（G1作为参考机）。

（1）当故障清除时间tc=0.01s时，仿真结果列于图2和图3。由图2可以看出，正则形变量z1和正则形变量z2的幅值都是衰减的，且z2比z1幅值衰减得更快。由图3可以看出，此时发电机转子角也都是衰减的，表明系统是稳定的。这和①的结论是相同的。

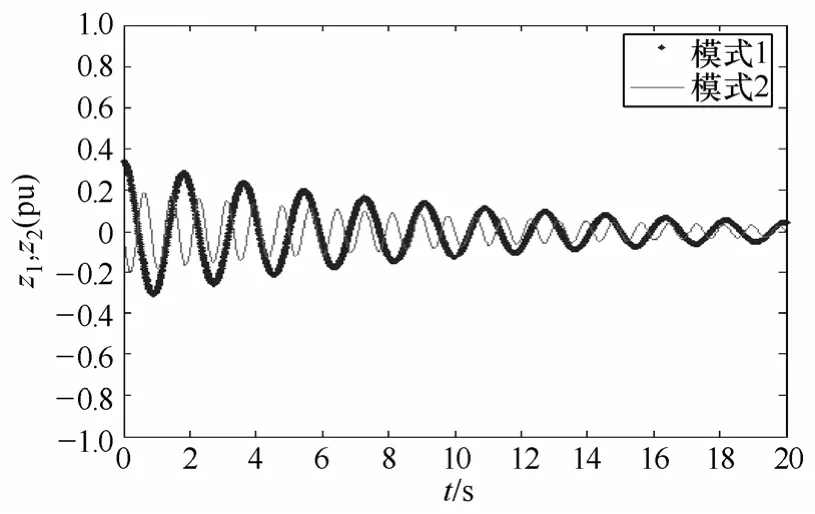
图2 正则形变量z1和z2的振荡曲线（tc=0.01s）Fig.2 Oscillations curves of z1 and z2（tc=0.01s）

图3 发电机转子角曲线(tc=0.01s)Fig.3 Rotor angles curves of the generators (tc=0.01s)

（2）当故障清除时间tc=0.09s时，仿真结果列于图4和图5。比较图2和图4可以看出，tc=0.09s时z2的幅值衰减比tc=0.01s时变慢，z1幅值的衰减也变慢，但没有z2幅值衰减变慢得快，在这种情况下很难区分z1和z2哪个更加稳定。

图4 正则形变量z1和z2的振荡曲线（tc=0.09s）Fig.4 Oscillations curves of z1 and z2（tc=0.09s）

图5 发电机的转子角度曲线(tc=0.09s)Fig.5 Rotor angles curves of the generators (tc=0.09s)

（3）当故障清除时间tc=0.11s时，仿真结果如图6和图7所示。由图6可以看出，z2的幅值增大，从而导致发电机转子角振荡发散（见图7），系统失稳。这和上面（3）的结论是相同的。

图6 正则形变量z1和z2的振荡曲线（tc=0.11s）Fig.6 Oscillations curves of z1 and z2（tc=0.11s）

图7 发电机的转子角曲线(tc=0.11s)Fig.7 Rotor angles curves of the generators (tc=0.11s)

6 结论

本文在正则形二阶变换基础上，充分考虑和利用正则形二阶变换过程中省略的交叉项和省略的三阶项，提出了分析大扰动下电力系统稳定的非线性稳定因子的新概念，即提出了阻尼因子和稳定域因子的新概念。通过阻尼因子可分析大扰动下正则形变量幅值的改变情况，通过稳定域因子可获得大扰动下正则形变量大致稳定的区域，进而判断大扰动下系统动态特性和稳定情况。对小扰动下的stressed系统，通常的特征分析方法无法适应其强非线性时，本文提出的方法同样适用。这些稳定信息从以往的分析理论和方法中是得不到的，这就从另一侧面为系统的稳定分析提供了一条可行途径。电力系统算例仿真结果证明了本文所提出非线性稳定因子这一新概念的正确性和在电力系统中应用的有效性。

由于实际大规模电力系统的复杂性，本文所提出的数学模型只是某种程度的近似。求解电力系统更高阶解析解，以及解决其在大规模电力系统中应用的维数灾问题将是下一步研究的重点。

[1] Dobson I, Barocio E. Scaling of normal form analysis coefficients under coordinate change[J]. IEEE Trans.on Power Syst., 2004, 19(3): 1438-1444.

[2] Zhu S Z, Vitta V, Kliemann W. Analyzing dynamic performance of power systems over parameter space using normal forms of vector fields part I:Identification of vulnerable regions[J]. IEEE Trans.on Power Systems, 2001, 16(4): 444-450.

[3] Saha S, Fouad A A, Kliemann W. Stability boundary approximation of a power system using the real normal form of vector fields[J]. IEEE Trans. on Power Syst., 2005, 12: 797-802.

[4] Starrett S K, Fouad A A. Nonlinear measures of mode-machine participation[J]. IEEE Trans. on Power Syst., 1998, 13(2): 389-394.

[5] 李伟固. 正则形理论及其应用[M]. 北京: 科学出版社, 2000.

[6] 邓集祥, 陈武晖, 纪静. 基于正则形理论的电力系统 2阶模态谐振的研究[J]. 中国电机工程学报,2006, 26(24): 5-11.

Deng Jixiang, Chen Wuhui, Ji Jing. Study on power system second order modal resonance on the basis of normal forms theory[J]. Proceedings of the CSEE,2006, 26(24): 5-11.

[7] Jang G, Vittal V, Kliemann W. Effect of nonlinear modal interaction on control performance use of normal forms technique in control design. Part Ⅰ:General theory and procedure[J]. IEEE Trans. on Power Syst., 1998, 13(2): 401-407.

[8] Sanchez Gasca J J, Vittal V, Gibbard M J, et al.Committee report-task force on assessing the need to include higher order terms for small-signal (modal)analysis[J]. IEEE Trans. on Power Syst. , 2005, 20(4):1886-1904.

[9] Betancourt R J, Barocio E, Arroyo J, et al. A real normal form approach to the study of resonant power systems[J]. IEEE Trans. on Power Syst., 2006, 21(1):431-432.

[10] Guckenheimer J, Holmes P. Nonlinear oscillations,dynamical systems and bifurcations of vector fields[M]. New York: Springer-Verlag, 1990.

[11] Kumano T. Nonlinear stability indexes of power swing oscillation using normal form analysis[J]. IEEE Trans. on Power Syst. , 2006, 20(2): 1439-1448.

[12] 邓集祥, 赵丽丽. 主导低频振荡模式二阶非线性相关作用的研究[J]. 中国电机工程学报, 2005, 25(7):15-21.

Deng Jixiang, Zhao Lili. Study on the second order nonlinear interaction of the critical inertial modes[J].Proceedings of the CSEE, 2005, 25(7): 15-21.