基于瞬时功率理论的新型功率方向元件

古 斌 谭建成

（1. 广西大学电气工程学院 南宁 530004 2. 绍兴文理学院工学院 绍兴 312000）

1 引言

目前可作为主保护且较成熟的方向纵联保护原理主要有[1]：工频突变量方向保护、负序方向保护。工频突变量方向保护通过模拟阻抗直接比较工频突变量电压、电流的极性（相位）以判别故障方向，保护的自适应性较强[2]，如不受过渡电阻影响，取母线侧电压时完全适用于串补线路等。负序方向保护通过比相算法计算负序电压、电流的相位差来判断故障方向。但这两种方向保护原理都是基于工频量，故将受非工频分量的影响，故障前和故障期间的非工频分量均将影响保护的快速性、选择性和灵敏性。由于电力系统的复杂性和故障发生的随机性,很难用十分有效的方法消除非工频分量的影响。另外基于工频变化量的方向保护原理虽然清晰、实现简单，但其最大不足是动作速度较慢。因此，研究高性能的方向继电器是继电保护领域中十分紧迫的任务，具有特别重要的意义[3]。

能量（功率）保护原理是近年来继电保护领域的研究热点之一[4-8]。瞬时无功功率理论是 20世纪80年代初由日本学者提出[9-10]，该理论适用于系统不对称或畸变及暂态过程，利用电压、电流瞬时值实时计算三相无功功率，目前已成功应用于无功补偿及有源滤波等诸多工程领域[11-13]。本文基于瞬时无功理论及故障分量保护原理，提出一种新型功率方向元件，该原理基于系统阻抗呈感性这一显著特征，直接利用线路两侧保护安装处的电压、电流瞬时值计算故障附加网络中的无功，区内故障时计算结果为两侧等效无源系统的无功，区外故障时为一侧系统无功及线路无功加该侧系统无功，并比较两侧计算结果来判定区内、区外故障，该原理物理意义明确，算法简单、易于实现，无需进行专门的滤波器设计，实时滤序算法[14]的引入，也使得该保护原理动作速度较快。由于是基于故障分量，所以该原理具有所有故障分量保护原理所具有的优点，如不受过渡电阻影响，适用于串补线路等。

2 三相瞬时无功功率及有关分析

由瞬时无功理论有[9-10]

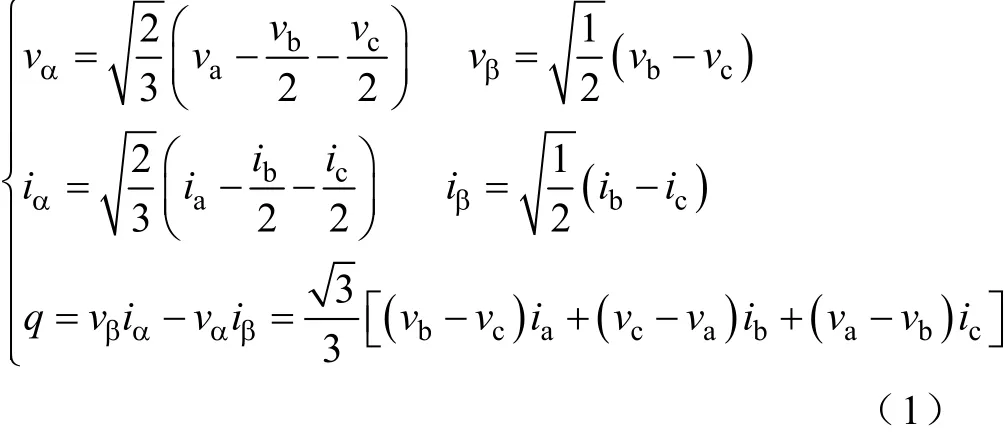
由于三相瞬时无功计算已自动滤除了零序，仅考虑正弦不对称时正、负序分量有

式中，V1、V2为正、负序电压有效值；φv1、φv2为A相正、负序电压初相角；I1、I2为正、负序电流有效值；φi1、φi2为A相正、负序电流初相角。

可见三相正弦不对称系统中三相瞬时无功直流分量为同序电压、电流作用而成；两倍频交流分量由不同序电压、电流作用而成。文献[11]给出了不对称且畸变情况下的三相瞬时无功表达式，表明其直流分量由电压、电流中同次（谐波次数）、同序分量作用而成，交流分量由同次不同序或同序不同次分量作用而成。如把三相电压、电流取为三相负载端口的值，则在三相正弦对称时三相瞬时无功功率q为定值，即为传统功率理论中负载的无功功率；在三相不对称或畸变时，q为一随时间变化的值，其一周波的平均值即直流分量为定值，因而三相瞬时无功功率q反映了三相电路作为一个整体某一时刻在三相电路之间来回传递的功率大小（负载无功功率的大小）[11]。

3 功率方向元件

对图1所示系统，根据叠加原理，系统发生故障后可分解成正常系统和故障分量系统。图2表示区内故障时的故障分量系统。M、N为系统等效无源网络，Δi、Δv为保护安装处电流故障分量和电压故障分量，UF(0)为故障前故障点的电压。

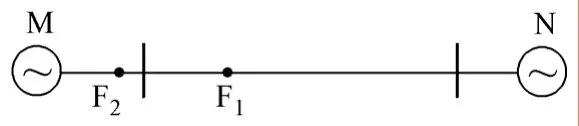
图1 系统图Fig.1 System model

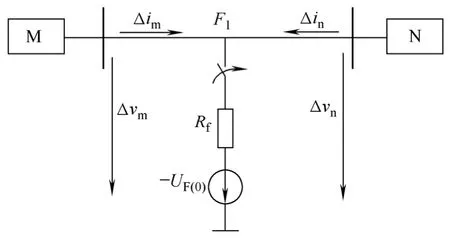
图2 正向故障时的故障分量系统Fig.2 A forward fault component system

对故障分量系统，由式（1）可计算两侧等效无源系统的无功为

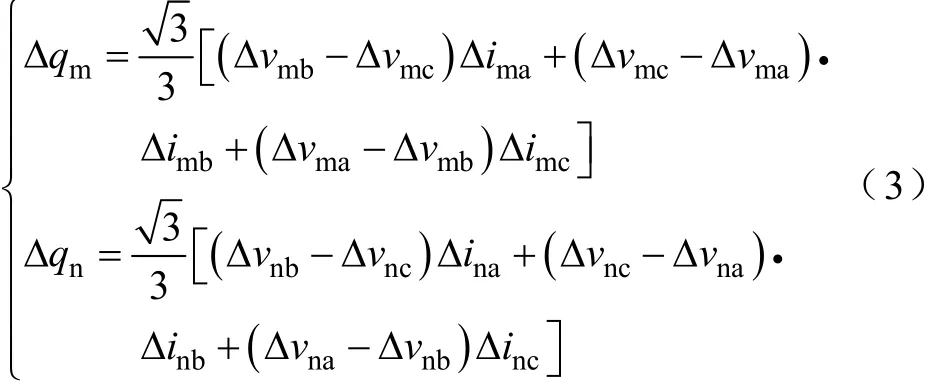
式中，T为工频周期（下同）；、为故障附加网络中两侧等效无源系统无功损耗的直流分量。本文附录中分析了发生各种故障时的情况，结论是：三相对称故障及两相接地故障时，为定值；单相接地故障及两相故障时，为零。可见用式（4）的突变量无功直流分量仅能判断三相故障及两相接地故障。观察式（1）及式（2），当M及N侧三相电压、电流采用负序分量时，可得两侧等效无源系统无功损耗负序分量的公式

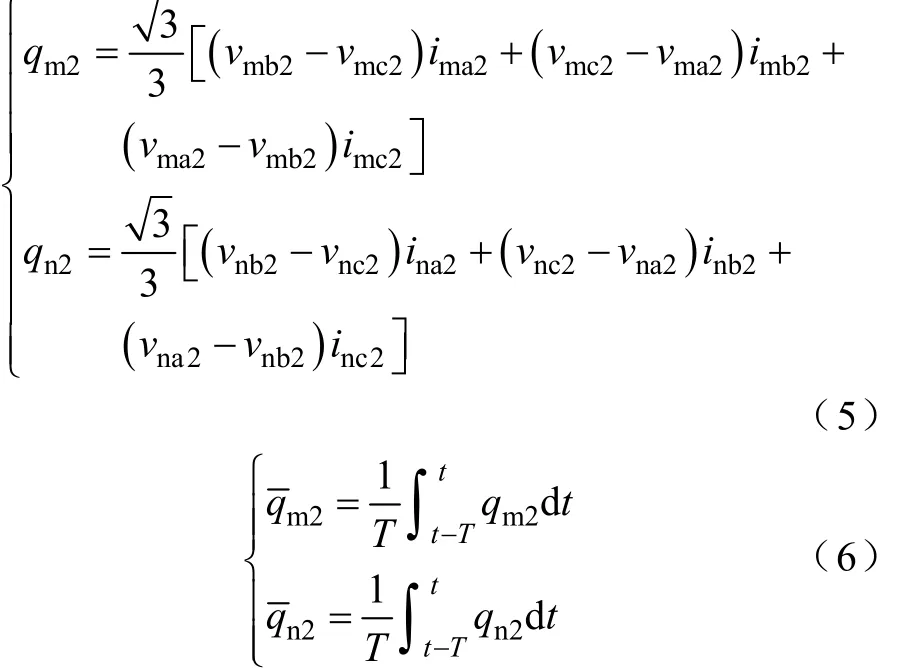
式中下标2表示负序量。即不对称故障时可由两侧系统的负序功率来判断故障方向。负序分量存在于故障的全过程，因此，负序无功方向纵联保护可以可靠地反应不对称故障的全过程。负序分量方向保护的主要缺点是被认为“不能可靠反应三相短路”[1]。但如果给负序无功方向元件配以突变量无功方向元件专门反应三相短路，则可以构成一种完善的纵联方向保护。

式（4）和式（6）的均值滤波可消除高频噪声的影响。区内故障时两侧无功计算结果为两侧系统等效阻抗的无功损耗；对区外故障（如图1系统F2点故障），N侧的无功计算结果仍为 N侧系统等效阻抗无功损耗，而M侧的无功计算结果为线路阻抗及N侧系统等效阻抗无功损耗之和。区内故障时两侧无功计算结果同号；区外故障时，考虑到图2所示的电流参考方向，两侧无功计算结果异号。

突变量算法为

式中，N为每周波采样点数。引用文献[14]的基于一个采样间隔的滤序算法，可得电压、电流的实时负序分量。 每工频周期采样 96个点的负序电流滤序算法为

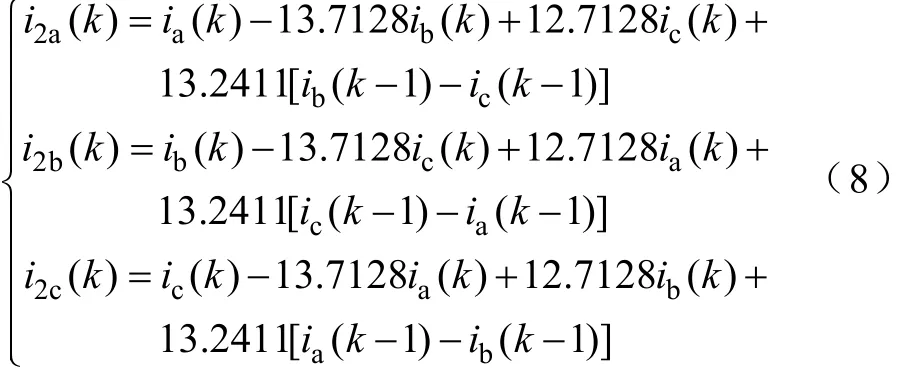
4 仿真结果及分析

为考核本文所提出的保护原理性能, 选用现场500kV超高压输电线路模型和实际参数[15]，仿真模型如图1所示。

两侧系统阻抗参数：

线路长度为500km，线路参数：

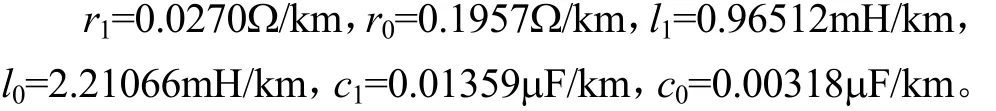
仿真中功率皆以标幺值表示，基准值为200MVA，突变量无功及负序无功为式（4）和式（6）的计算结果，故障过渡电阻表示为Rf，A相故障角为α。在仿真图中的波形图标为：◇—A相或M侧，□—B相或N侧，△—C相。仿真计算的部分结果如图3～图6所示（区内故障点距M侧100km，区外故障于M侧反向出口故障）。

式（2）是基于电流流进系统为正方向，仿真时取母线指向线路即流出系统为电流正方向（如图 2所示），功率符号与式（2）的表达相反。由式（5）和式（8）可知，如保护所采用的软硬件能够保证在一个采样时间间隔内对所有算法进行一次循环，不考虑暂态分量的影响，则负序无功方向元件能够保证在一个采样时间间隔的数据窗内做出判断，几乎达到了最优速度。从仿真图还可看出，从故障起始两侧功率计算值就已表现出了故障方向特征（区内故障同号，区外故障异号），两侧功率计算值在故障后一工频周期内达到稳定，因而该功率方向元件动作速度快，可在故障后半个周期内准确可靠动作。另外，由式（2）、式（4）及式（6）知，每一采样点判据计算结果都有相当于故障分量电压、电流幅值乘积的稳定输出，这也大大提高了保护的动作可靠性。

图3 Rf=100Ω, α=90°时单相接地故障Fig.3 One phase to ground fault

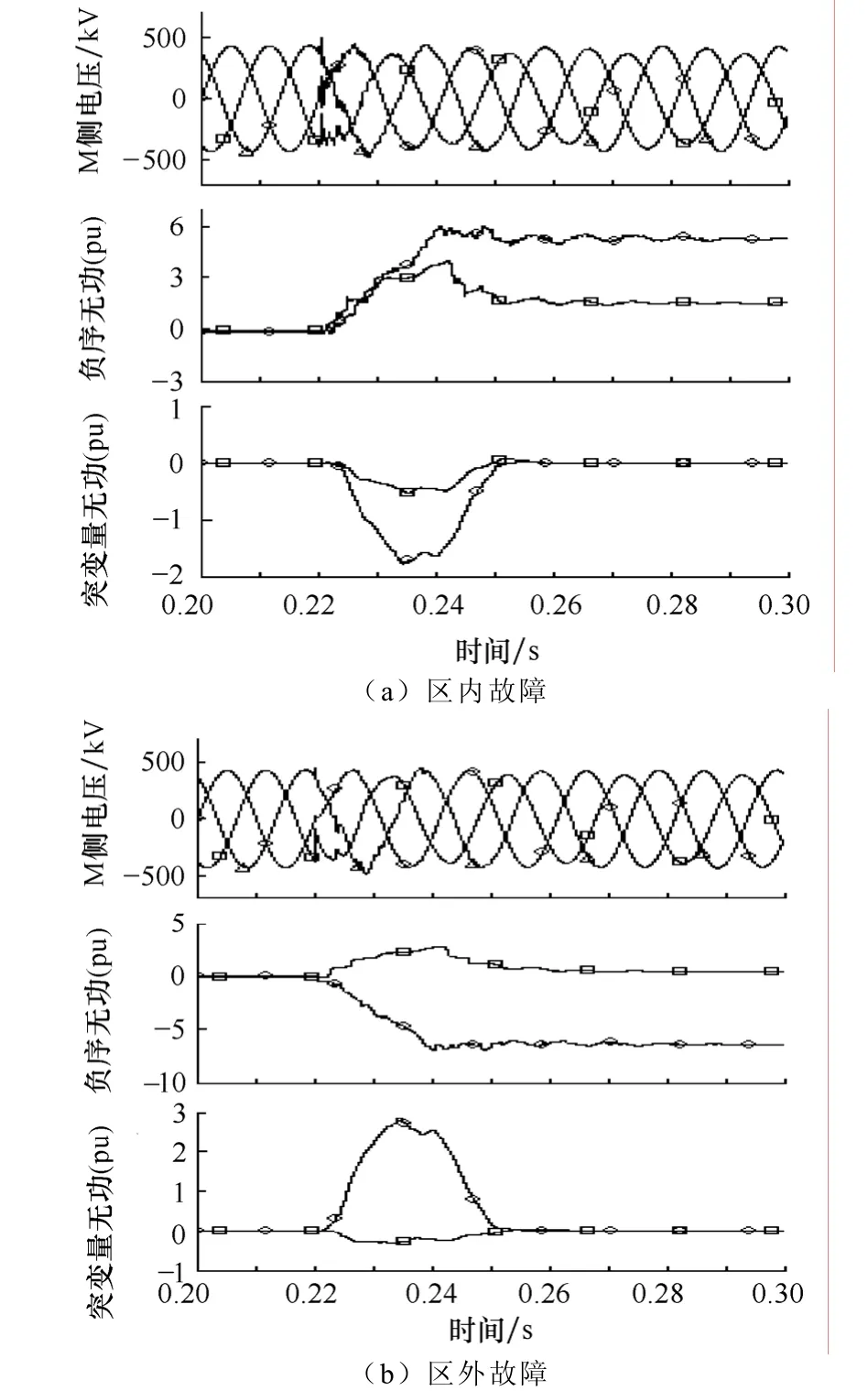
图4 Rf=100Ω, α=0°时两相接地故障Fig.4 Two phases to ground fault

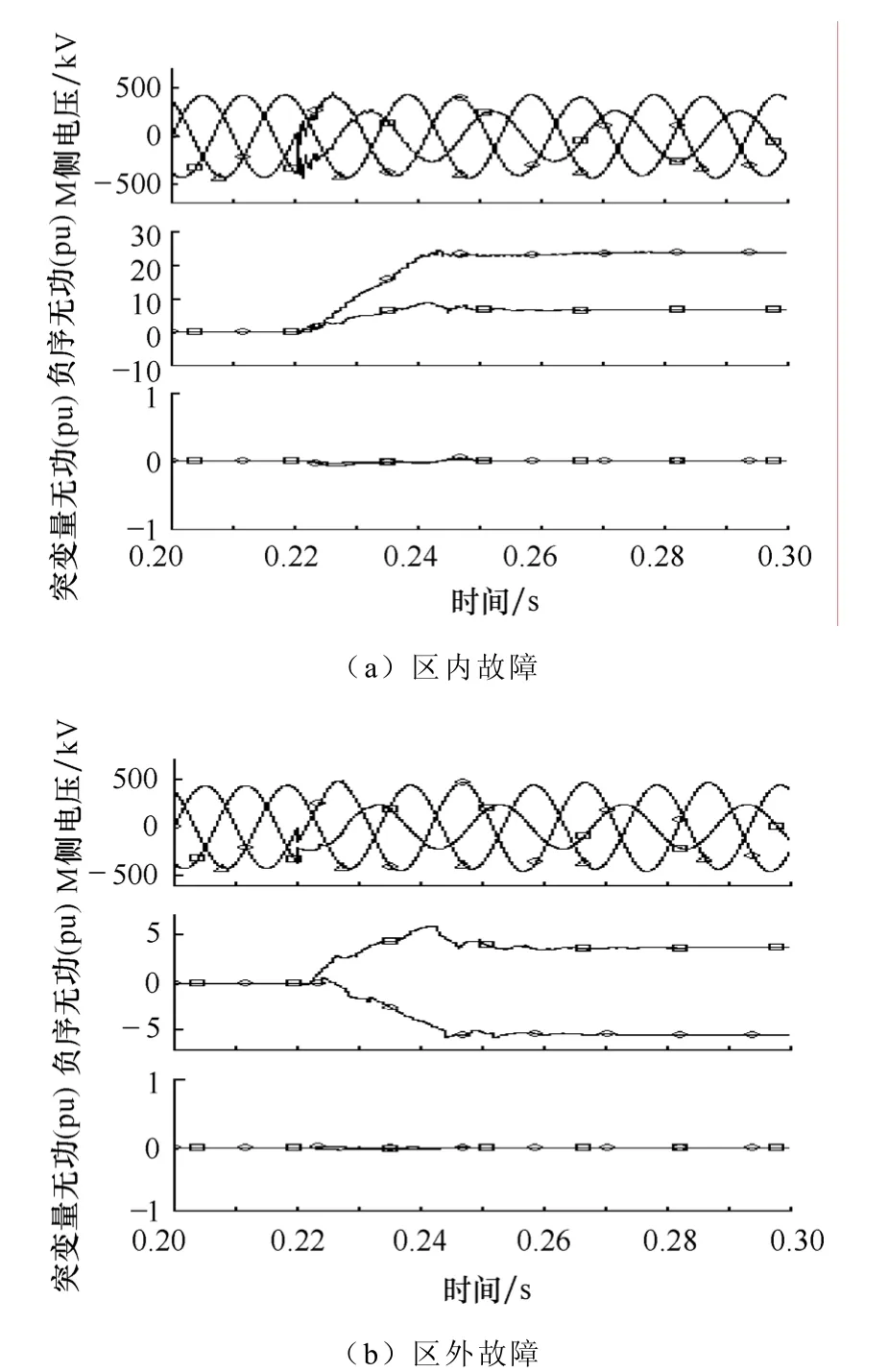
图 5 Rf=100Ω, α=0°时两相故障Fig.5 Phase to phase fault

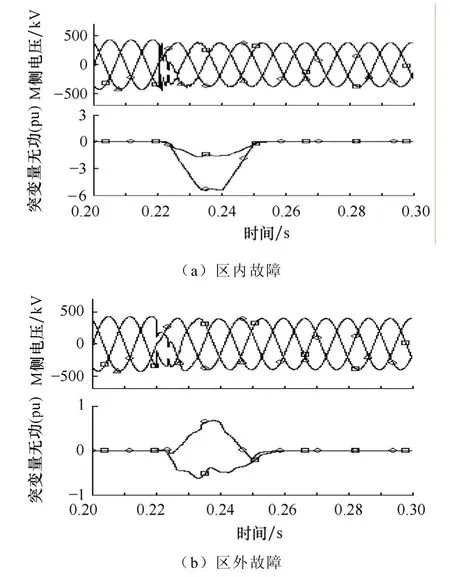
图 6 Rf=100Ω, α=0°时三相故障Fig.6 Three phases to ground fault

5 结论

基于瞬时功率理论，本文提出了一种新型功率方向保护原理，该原理由负序无功方向元件及突变量无功方向元件构成，两者构成了一种完善的纵联保护。分析了该继电器在不同种类的短路故障中的动作特性及方向继电器的性能，从而明确了新算法在理论上的正确性。对各种区内、区外故障进行了仿真实验，结果显示该新型功率方向保护原理在各种故障下可在故障后半周期内可靠动作，仿真结果同时显示该新型功率方向元件也具有较高的灵敏性。

附 录

各种区内不对称故障附加网络如附图 1～附图 3所示。现分析M侧Δq的情况，仅考虑工频情况时有

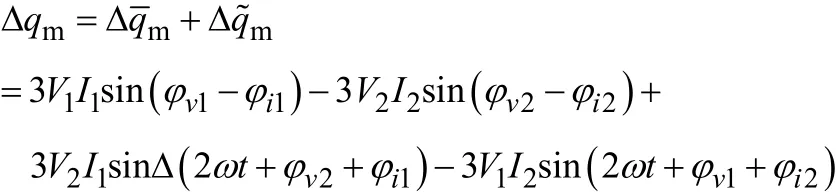
即

式中，V1、I1为 M侧电压、电流正序故障分量有效值；V2、I2为M侧电压、电流负序分量有效值。

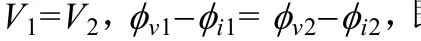
附图1 单相接地故障附加网络App. Fig.1 The superimposed fault network for phase to ground fault

附图2 两相接地故障附加网络App. Fig.2 The superimposed fault network for two phase to ground fault

附图3 两相故障附加网络App. Fig.3 The superimposed fault network for phase to phase fault

附图4 参数示意图App. Fig.4 The parameters skech

考虑三相不对称且畸变，由本文第 3节知，不对称且畸变情况下的三相瞬时无功直流分量由电压、电流中同次、同序分量作用而成，因而

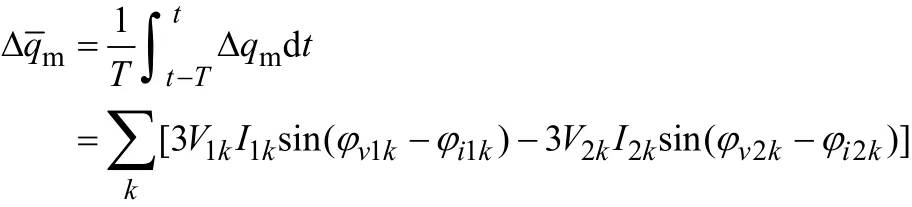
式中，k为谐波次数；下标1表示正序，2表示负序。其不同故障时的结果与工频时一致。

[1] 贺家李, 李永丽, 李斌, 等. 特高压输电线继电保护配置方案(二)——保护配置方案[J]. 电力系统自动化, 2002, 26(24): 1-6.

He Jiali, Li Yongli, Li Bin, et al. Relay protection for UHV transmission lines: part two disposition of relay protection[J]. Automation of Electric Power Systems,2002, 26(24): 1-6.

[2] 戴学安. 继电保护原理的重大突破——综论工频变化量继电器[J]. 电力系统自动化, 1995, 19(1): 41-47.

Dai Xuean. A brief discussion on the protection relay based on power frequency variation principle[J].Automation of Electric Power Systems, 1995, 19(1):41-47.

[3] 袁荣湘, 陈德树, 张哲. 高压线路方向保护新原理的研究[J]. 中国电机工程学报, 2000, 20(3): 20-25.

Yuan Rongxiang, Chen Deshu, Zhang Zhe. Study on a new algorithm for the high voltage line [J].Proceedings of the CSEE, 2000, 20(3): 20-25.

[4] 何奔腾, 金华烽, 李菊. 能量方向保护的实现和试验[J]. 中国电机工程学报, 1997, 17(3): 171-174.

He Benteng, Jin Huafeng, Li Ju. Realization and test of the energy directional protection [J]. Proceedings of the CSEE, 1997, 17(3): 171-174.

[5] 何奔腾, 金华烽, 李菊. 能量方向保护原理和特性研究 [J]. 中国电机工程学报, 1997, 17(3): 166-170.

He Benteng, Jin Huafeng, Li Ju. Principle and property research of the energy directional protection[J]. Proceedings of the CSEE, 1997, 17(3):166-170.

[6] 文明浩, 陈德树, 尹项根. 远距离输电线路的能量平衡保护[J]. 中国电机工程学报, 2001, 21(2):74-79.

Wen Minghao, Chen Deshu, Yin Xianggen. Long transmission line protection based on the principle of balance of energy[J]. Proceedings of the CSEE, 2001,21(2): 74-79.

[7] Darwish H A, Taalab A M, Ahmed E S. Investigation of power differential concept for line protection[J].IEEE Transactions on Power Delivery, 2005, 20(2):617-624.

[8] Namdari F, Jamali S, Peter A C. Differential protection of busbars and transmission lines based on the energy conservation law for wide area protection[J]. Automation of Electric Power Systems,2007, 31(3): 35-40.

[9] Akagi H, Kanazawa Y, Nobase A. Generalized theory of the instantaneous reactive power in three-phase circuits[C]. Proceedings of International Conference on Power Electronics, Tokyo, Japan, 1983.

[10] Akagi H, Kanazawa Y, Nobase A. Instantaneous reactive power compensators comprising switching devices without energy storage components[J]. IEEE Transactions on Industry Applications, 1984, 20(3):625-630.

[11] 刘进军, 王兆安. 瞬时无功功率与传统功率理论的统一数学描述及物理意义[J]. 电工技术学报, 1998,13(6): 6-12.

Liu Jinjun, Wang Zhaoan. Uniform mathematical description of instantaneous reactive power theory and conventional power theory and its physical meaning[J]. Transactions of the Electrotechnical Society, 1998, 13(6): 6-12.

[12] Willems J L. A new interpretation of the Akagi-Nabae power components for nonsinusoidal three-phase situations[J]. IEEE Transactions on Instrumentation and Measurement, 1992, 41(4): 523-527.

[13] Aller J M, Bueno A, Restrepo J A. Advantages of the instantaneous reactive power definitions in three phase system measurement[J]. IEEE Power Engineering Review, 1999, 19(6): 54-56.

[14] Bo Z Q. Adaptive non-communication protection for power lines, BO scheme 3—The accelerated operation approach[J]. IEEE Transactions on Power Delivery,2002, 17(1): 97-104.

[15] 毛鹏, 杨立, 杜肖功. 基于零序分量的距离继电器[J]. 电力系统自动化, 2003, 27(10): 60-65.

Mao Peng, Yang Li, Du Xiaogong. Study of the distance relay based on zero sequence components[J].Automation of Electric Power Systems, 2003, 27(10):60-65.