长江下游典型代表性潮型选择研究初探

夏云峰，闻云呈，梁 婷

（南京水利科学研究院，南京210024）

长江大通至吴淞口全长约567 km，为长江口以上受潮汐影响区段。其中大通至江阴为潮区界至潮流界的近口段414 km，河道平面形态多为分汊和缩窄相间的藕节状。江阴至吴淞口约153 km，为长江潮流界以下的河口段，长江自江阴鹅鼻嘴以下江面展宽，江中洲滩群生，汊道众多，分为澄通河段、白茆沙河段。福姜沙河段位于长江口潮流界变动区江阴以下澄通河段，属长江河口河流段。进口鹅鼻嘴处江面宽1.4 km，河床窄深，至长山江面放宽至4.1 km，其后福姜沙分左右两汊，右汊为鹅头型弯道，长约22.2 km，江面宽约950 m，分流比约为20%；左汊顺直，为主汊，江面宽约3 km，长约19 km，分流比约为80%。长江主流由鹅鼻咀导流岸壁导入福姜沙左汊，福姜沙左汊下段又被双涧沙分为福北水道和福中水道，水流走福中水道至福姜沙尾和福南水道汇合，进入浏海沙水道，部分水流由双涧沙北水道进入如皋中汊。如皋中汊为左汊，长约10 km，江面宽850～1 000 m，分流比约为30%，右汊浏海沙水道江面宽约2 500 m，分流比约为70%，至老海坝下侧九龙港一带与浏海沙水道汇合，此处江面宽约1.6 km。其后长江主流紧贴南岸，经九龙港至十二圩港，脱离南岸过渡到南通姚港至任港一带，主流紧贴左岸顺通州沙东水道下泄。本河段位于长江口潮流界变动区，属河口河流段，受上游径流及下游潮汐影响，水流条件复杂，河床沙细易动［1］。

图1 大通至河口长河段示意图Fig.1 Sketch of river reach from Datong to estuary

1 水流、泥沙特性

1.1 径流条件

长江下游最后一个水文站大通站距工程河段长400 km，根据大通水文站资料（1950～2003年），历年平均年径流量为9 250×109m3；历年最大流量为92 600 m3/s（1953-08-01）；历年最小流量为4 260 m3/s（1979-01-31）；多年平均流量为 28 700 m3/s。

1.2 潮汐和潮流

长江口为中等强度潮汐河口，本河段潮汐为非正规半日浅海潮，每日两涨两落，且有日潮不等现象，在径流与河床边界条件阻滞下，潮波变形明显，涨落潮历时不对称，涨潮历时短，落潮历时长，潮差沿程递减，落潮历时沿程递增，涨潮历时沿程递减。长江口潮流界随径流强弱和潮差大小等因素的变化而变动，枯季潮流界可上溯到镇江附近，洪季潮流界可下移至西界港附近。

1.3 泥沙条件

该河段泥沙主要为流域来沙，悬沙中值粒径范围为0.001～0.025 mm。主槽内粒径较粗，悬沙基本不含0.01 mm以上细沙。河床质分析表明，本河段底沙主要是细沙。主槽床沙较粗，中值粒径d50为0.13～0.25 mm，河心沙滩滩面d50约为0.1 mm。福南水道深槽河床质中值粒径约为0.17 mm，福南水道北边滩d50为0.01～0.02 mm；福姜沙北汊深槽d50约为0.18 mm，北汊边滩d50为0.014～0.017 mm。可见本河段的滩槽冲淤变化以床沙推移运动和临底悬沙造床作用为主。

2 一维水流、泥沙数学模型建立及验证

2.1 水流运动基本方程

式中：t为时间坐标；x为空间坐标；Q为流量；Z为水位；u为断面平均流速；n为糙率；A为过流断面面积；B为主流断面宽度；BW为水面宽度（包括主流断面宽度B及仅起调蓄作用的附加宽度）；R为水力半径；q为旁侧位流流量［2-3］。

2.2 泥沙输移基本方程

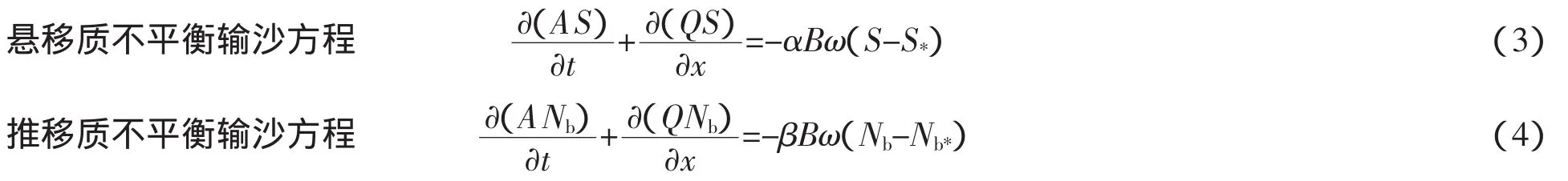
式中：Q为流量；A为过流断面面积，B为主流断面宽度；S和S觹分别为断面平均含沙量及挟沙能力；Nb和Nb*分别为水深范围内平均推移质输沙率和推移质输沙能力；ω为沉速；α和β为泥沙恢复饱和系数［4］。

2.3 河床冲淤变形方程

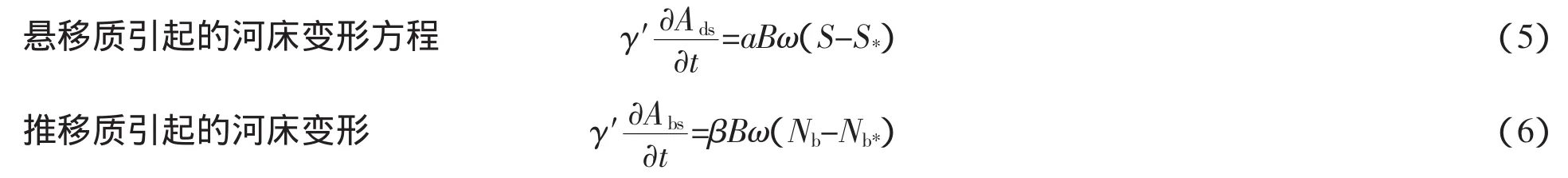
式中：γ′为淤积物干容重；Ads为悬移质引起冲淤变化面积；Abs为推移质引起冲淤变化面积［5］。

2.4 模型的验证

数学模型计算范围上起安徽大通，下迄长江口，上游控制边界为大通站，下游控制边界长江北支为连兴港站，南支在南北港的六效附近［6］。

本文对工程河段洪枯季水动力、泥沙条件以及河床冲淤进行了验证，计算结果与实测值较一致（图2～图5），结果表明一维数学模型较好地模拟了洪、枯季条件下径流下泄、潮波沿程传播、潮流运动以及泥沙输移特性。

3 潮汐特性初步分析及典型代表性潮型选择

3.1 计算河段沿程各潮位站潮位径流量相关分析

由于计算河段位于长江下游潮流界变动区以下，受上游径流和下游潮汐共同作用，其沿程潮波传播和潮流运动较复杂。为确定河段典型代表性水流运动和潮波特性，根据所处河段和计算控制边界，特选取江阴站、天生港站和六效站来分析高潮位和日平均潮位与上游来流的关系，分析时考虑大通站径流下泄运动时间为2～3 d，其中大通流量与日平均潮位关系曲线见图6。各潮位站高潮位及日平均潮位和上游径流的相关系数见表1。

由表1可知，江阴站的相关系数相对较大，表明江阴站附近河段潮位受上游径流影响较大。而六效站的相关系数较小，表明上游径流对接近河口河段潮位影响较小。

图2 枯季水位验证Fig.2 Verification of water level in dry season

图3 洪季大潮流量验证图Fig.3 Verification of flux of spring tide in flood season

图4 枯季含沙量验证图Fig.4 Verification of sediment concentration in dry season

图5 枯季输沙率验证Fig.5 Verification of sediment transportation rate in dry season

表1 各潮位站高潮位及日平均潮位和上游径流量相关系数R2Tab.1 Correlation coefficient between high tide level and daily average tidal level with the runoff of upper reaches in each station

图6 大通流量与日平均潮位相关关系曲线Fig.6 Correlation between Datong flux and daily average tidal level

3.2 六效站和连兴港站潮差累积频率分析

作为计算模型控制边界，典型代表性潮型的选择既要考虑潮位高低，更要关注潮差的大小。潮差的大小反映了潮汐动力的强弱即涨落潮流速的大小，通过六效和连兴港潮差累积频率分析，计算出不同频率的潮差大小，其特征潮差见表2。

3.3 典型代表性潮型和径流组合方案分析

考虑到长江上游流量的变化对长江口潮位有一定的影响，通过选定的相应潮差和上游洪季造床流量55 000 m3/s及枯季平均流量16 800 m3/s对应潮型，来确定典型的洪枯季代表性潮型（图7～图8）。

根据《海岸与河口潮流泥沙模拟技术规程》的要求，宜选择潮差中等偏大的潮型作为代表性潮型，分析其下游潮汐过程对该河段河床冲淤变化的影响。为此选择了潮差累积频率为50%、85%、95%代表性潮型作为比选的3种计算条件，分别表示为A，B，C三个方案，计算时间段为1998年9月～2000年12月，各区段河床冲淤变化计算结果见表3。

由表3可知，镇江以上河床冲淤变化主要受上游径流影响，下游潮汐的变化对河床冲淤变化影响甚小；镇江至江阴段河床冲淤变化主要受径流造床控制，冲淤特性基本一致，冲淤数量受潮汐影响。从3个方案的计算结果来看，工程河段受潮汐影响较明显，其中B方案和实测控制潮型计算结果较吻合，由此可见，依据85%潮差所选择的典型代表性潮型能基本反映计算河段河床冲淤变化。

图7 洪季代表性潮型曲线图Fig.7 Curve diagram of representative tidal type in flood season

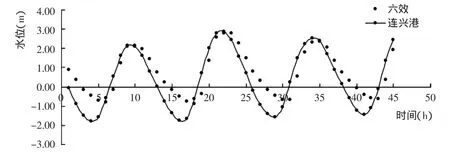
图8 枯季代表性潮型曲线图Fig.8 Curve diagram of representative tidal type in dry season

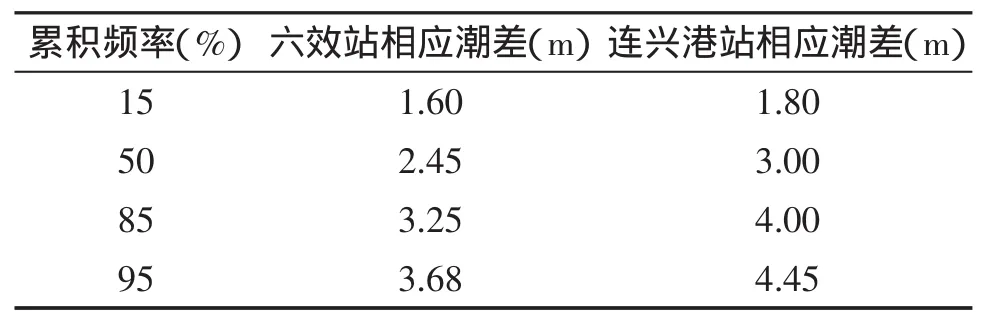
表2 六效和连兴港相应潮差及其累积频率Tab.2 Corresponding tidal difference and cumulative frequency of Liuxiao and Lianxinggang

表3 各代表性潮型方案计算各区段河床冲淤变化Tab.3 River bed erosion-deposition variation of representative tidal type in each river reach 亿m3

4 结论

本文建立了长江下游大通至长江口一维非恒定非平衡非均匀水流泥沙数学模型，并对其进行水动力条件和泥沙条件验证。结果表明，本模型建立及离散求解和有关参数选取是可行的，可用来进行相关水沙控制条件的比选计算，并为物理模型提供相应的边界控制条件。

下游各潮位站径流量和潮位相关分析表明，上游径流对计算河段潮位影响较明显，相关系数较大；随着向长江河口趋近，相关系数越来越小，潮位受径流影响进一步减弱。说明该河段水流运动及潮波传播受上游径流和长江口潮波共同作用，也反映了该河段水动力条件的复杂性。

不同代表性潮型方案计算结果表明，镇江以上造床作用主要受上游径流控制；镇江—江阴河段造床作用以径流为主，受潮汐影响较小；河段河床冲淤变化受径流和潮汐共同作用。下游中等偏大潮差的典型代表性潮型和上游径流组合基本反映计算河段河床冲淤变化。

［1］方波.长江下游大通—镇江河道干流水流挟沙力公式［J］.人民长江，2004，35（12）：42-44.FANG B.The formula of main stream sediment carrying force from Datong to Zhengjiang in lower Yangtze rive［rJ］.Yangtze River，2004，35（12）：42-44.

［2］杨国录，吴卫民.一维河流数值模拟算法的概述［J］.泥沙研究，1995（4）：34-41.YANG G L，WU W M.Resume of numerical modeling for one-dimension river mode［lJ］.Journal of Sediment Research，1995（4）：34-41.

［3］李义天，尚全民.一维不恒定泥沙数学模型研究［J］.泥沙研究，1998（1）：81-87.LI Y T，SHANG Q M.Modeling of sediment transport in unsteady flow［J］.Journal of Sediment Research，1998（1）：81-87.

［4］张瑞瑾，谢鉴衡.河流泥沙动力学［M］.北京：水利电力出版社，1989.

［5］窦国仁，赵士清.三峡水库变动回水区二维全沙数学模型的研究和初步应用［M］.武汉：武汉工业大学出版社，1993.

［6］夏云峰.感潮河段三维水流泥沙数学模型研究［D］.南京：河海大学，2002.