基于Copula函数的甬江流域设计潮位过程研究

薛晓鹏，张卫国，朱从飞，赵思远，郝振纯

(1.宁波市水利水电规划设计研究院，浙江 宁波 315192；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098)

甬江流域地处宁波市，位于我国东海岸，为独流入海的小流域，流域内最大的排洪河道——甬江在镇海口直接与外海相连，城市防洪易受潮汐影响。镇海站设计潮位过程是影响宁波市城市河道堤防设计的主要因素，因此研究镇海站设计潮位对宁波市城市防洪具有重要意义。目前工程设计中多采用设计高潮位与设计潮差同频率放大的方法，选取典型潮型，然后将高潮位和潮差按照设计值缩放典型潮型。但是这种方法没有考虑设计高潮位与潮差的遭遇可能性大小。

研究不同水文系列遭遇频率常用多维联合分布的方法。目前，多维联合分布模型的研究和应用已经比较成熟，Copula函数因形式多样且易于求解，广泛地应用在水文系列的多维联合分析中。比如，杨志勇等[1]采用Copula函数拟合降水距平百分率序列，计算出滦河流域各站点旱涝组合事件发生的概率；张冬冬等[2]采用Copula函数探讨洪水多要素的联合概率分布和条件概率分布；李天元等[3]构造了分别金沙江和岷江2江洪峰流量的单参数和双参数Copula联合分布，表明双参数Copula函数拟合效果优于单参数Copula函数。黄锋华等[4]研究分析了东江干支流年最大洪水遭遇风险特征，结果表明：Copula函数能较好地拟合东江干支流年最大洪水(出现时间和量级)联合分布。但是，目前的研究多停留在探究水文系列联合分布上，对应用高潮位与同期潮差联合分布推求潮位过程线的研究尚显不足。

1 高潮位与同期潮差组合分析方法

1.1 二维Copula联合分布模型L

1.1.1 边缘分布函数

设年最高潮位为Z，与之相对应的统一潮位过程的较大潮差为R，根据统计特性，假定年最高潮位和同期潮差分别服从Gumbel分布和正态分布，其分布函数分别为：

FZ(z)=exp {-exp [-(z-μ)/σ]}

(1)

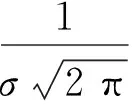
s

式中：μ、σ为统计参数，可用极大似然法对其进行估计。

对于假设的Gumbel分布和正态分布是否符合实际要求，需要对其进行假设检验。对于年最高潮位的Gumbel分布检验常使用K-S检验法，指标的表达式见式(3)；国际标准化组织组织统计学家对几十种正态性检验方法进行比较后，认为Wilk-Shapiro的W检验效果最好[5]。因此选用W检验来判断同期潮差的分布是否符合正态分布，指标表达式见式(4)。

K-S检验：

Dn=max {|F(x)-Fn(x)|}

(3)

式中：Fn(x)=i/(n+1)是等于或小于x的所有观察结果数目；F(x)表示理论分布的累积概率分布函数。

W检验：

(4)

当W>Wα=0.05时，认为在α=0.05的水平上不拒绝正态性假设。

1.1.2 二维Copula联合分布模型

Copula函数的优点在于分别考虑了变量的边缘分布和变量间的相关性结构，且能描述变量间的非线性相关关系。目前在水文领域常用的Copula函数主要有：Gumbel-Hougaard Copula函数、Clayton Copula函数、Frank Copula函数和AMH Copula函数。这4种Copula函数各有特点，可以描述各种相关关系的水文系列。

Copula 函数的参数θ可由Kendall 秩相关系数来推算。Kendall 秩相关系数用来描述年最高潮位和同期潮差之间的相依关系，计算公式为：

(5)

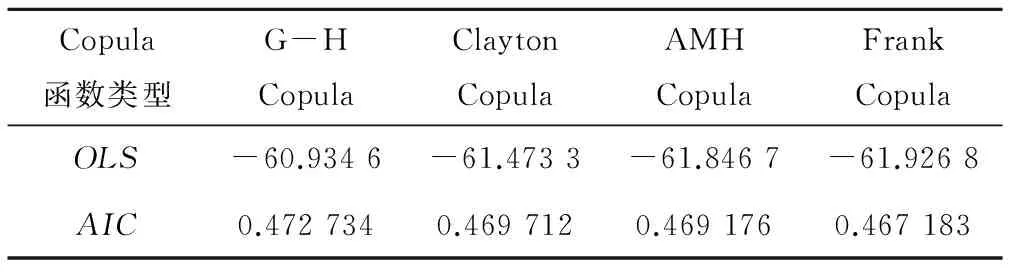
式中：τ为 Kendall秩相关系数，-1≤τ≤1，τ的绝对值越大表示变量间的相关关系越强；xi-xj为实测点据；n为系列长度。

4种常用的Copula函数表达式及Kendall秩相关系数τ与Copula 函数的参数θ间的关系见表1。

1.1.3 拟合优度评价

上述4种Copula函数对变量间相关性的描述各有特点，可通过拟合优度评价选择最优Copula 函数。常用的拟合优度评价方法有以下3种：

表1 常见的Copula函数及Kendall秩相关系数τ与 θ间的关系Tab.1 Common Copula functions and the relationship betweenrank correlation coefficients τ and θ

注：u和v均为边缘分布函数，u=FZ(z)，v=FR(r)；θ为Copula函数的参数；τ为 Kendall 秩相关系数。

(1)最小二乘法评价(OLS)。

(6)

(2)最小信息准则(AIC)。

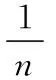
(7)

AIC=nlnMSE+2k

(8)

式中：Femp(xi,yi)为经验频率；C(ui,vi)为理论频率；k为模型参数的个数。

计算出的OLS或MSE越小，说明拟合优度越高。

(3) 理论联合概率与经验联合频率比较。绘制由理论联合分布和实测点据计算所得的经验联合分布的散点图进行比较。如果图上的点都落在45°线附近，表明所选的Copula函数拟合效果良好。经验联合分布的计算公式为：

(9)

式中：xi,yi为实测点据；nm,k为同时满足X≤xi,Y≤yi时联合观测值的个数；n为联合观测值的总个数。

1.2 设计组合风险分析

在防洪设计中，影响安全的主要因素是高潮位。当设计标准的高潮位发生时，相应出现的潮差有多种可能，且不同的潮差出现的概率也不相同。因此需研究选定设计高潮位时，不同频率潮差与之组合的概率风险情况。在满足设计高潮位z条件下，将潮差超过r发生的概率作为其组合风险率：

(10)

式中：Z和R分别为高潮位和潮差变量；FZ(z)为高潮位的边缘分布函数。

1.3 条件最可能组合

设计潮位过程的确定需要确定高潮位与潮差的组合方式，即需在给定高潮位Z的条件下，确定高潮位对应的最大潮差R。当高潮位一定时，每一个可能的同期潮差对应的概率分布为：

(11)

相应的条件密度函数为：

fR|Z(r)=cθ(u,v)fR(r)

(12)

式中：cθ(u,v)为Cθ(u,v)的密度函数；fR(r)为FR(r)的密度函数。

当条件概率密度fR|Z(r)取到最大值时，对应的高潮位与潮差组合(z,r0)即称为条件最可能组合，r0称为条件最可能潮差。此外，可以给定某个显著性水平α，计算得到条件最可能同期潮差r0的区间估计[r1,r2]，通过区间估计可以定量评价条件最可能同期潮差的不确定性。

2 镇海站设计潮位过程计算

2.1 年最高潮位与同期潮差二维联合Copula联合分布模型

选取镇海站1971-2015年实测潮位系列，假定年最高潮位服从Gumbel分布，同期潮差服从和Normal分布，对边缘分布函数的参数进行最大似然估计，结果见表2。

表2 边缘分布函数参数最大似然估计值Tab.2 Maximum likelihood estimation of marginaldistribution function parameters

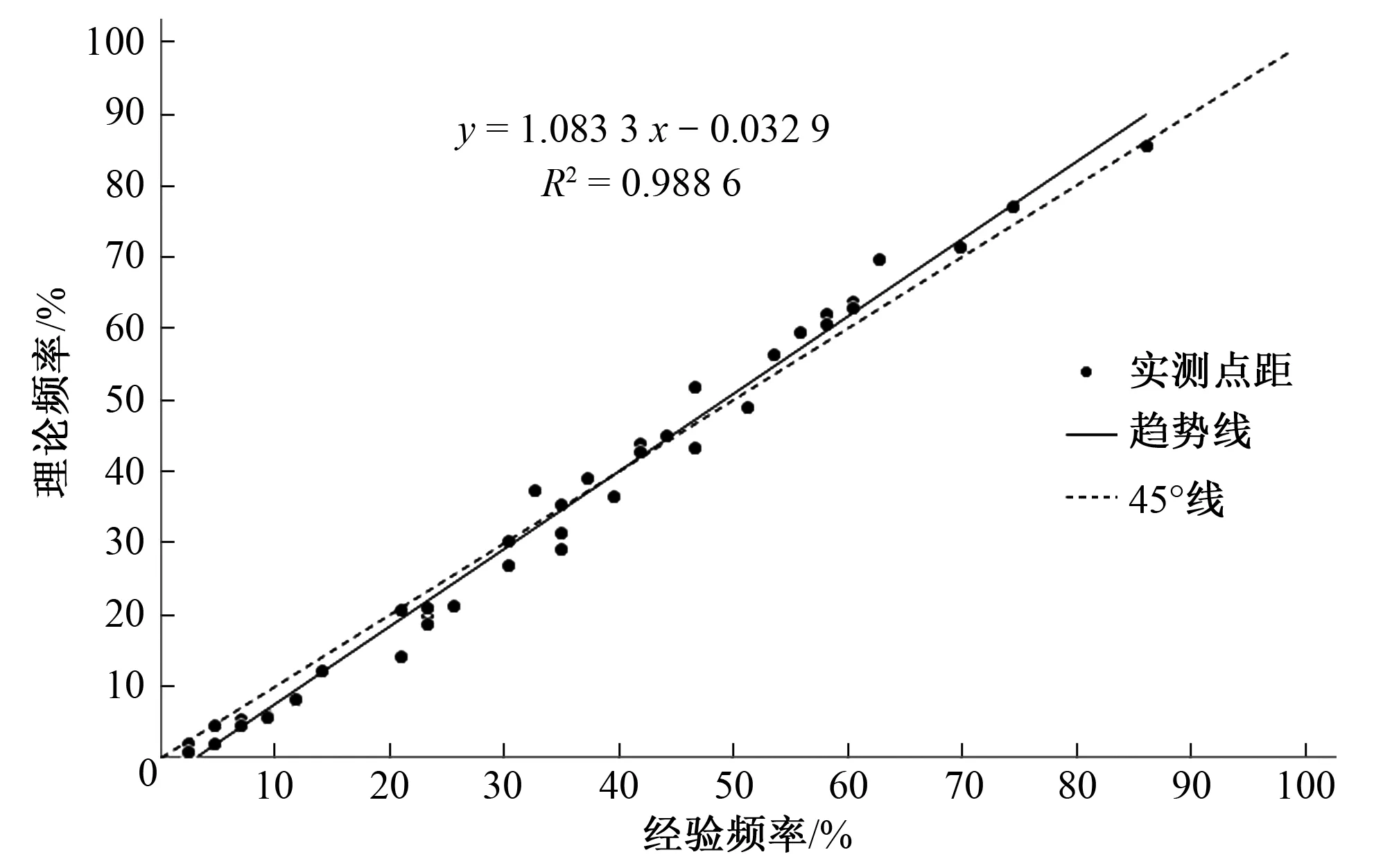
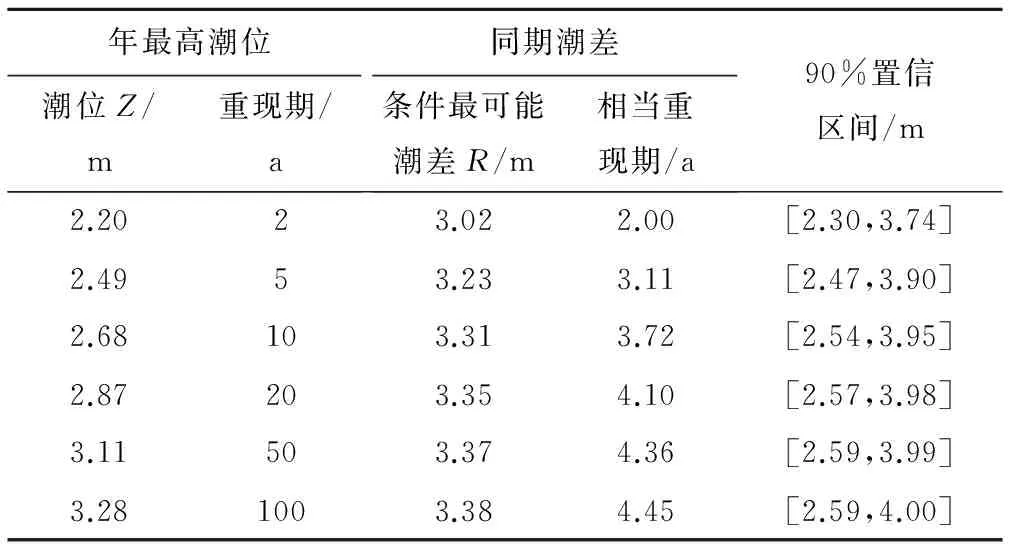
对Gumbel分布函数进行K-S检验，计算得到Dn=0.023 78，查表得Dα=0.05n=42=0.209 85，易知Dn

对Normal分布函数进行W检验，计算得到W=0.967 998，查表Wα=0.05=0.942(n=42)，易知W>Wα=0.05，因此在α=0.05水平上潮差分布不拒绝正态性假设。

因此，认为在 0.05 的显著水平时，年最高潮位服从 Gumbel 分布，同期潮差服从正态分布。图1、图2分别为年最高潮位和同期潮差的概率分布图，可以看出，各单变量的理论分布与经验点据均拟合良好，证明采用的分布函数合理。

图1 年最高潮位理论分布与经验分布对比Fig.1 Comparison of theoretical distribution and empirical distribution of annual maximum tidal levels

图2 同期潮差理论分布与经验分布对比Fig.2 Comparison of tidal theoretical distribution and the empirical distribution over the same period

为了计算Copula函数的参数θ，首先根据式(5)计算得到秩相关系数τ=0.277 962，可见2者为弱正相关关系。由 Kendall 秩相关系数分别求出4种Copula函数的参数值，见表3。

表3 4种Archimedean Copula的参数θ值Tab.3 The parameter θ value of four kinds ofArchimedean Copula functions

为选择最优Copula 函数，根据式(6)～(8)对计算出4种Copula函数的优选度评价指标见表4。

表4 4种Copula函数的优选度评价指标Tab.4 Optimization index of four kinds of Copula functions

由表2可看出Frank Copula的OLS与AIC值均最小，因此选用Frank Copula拟合程度最好。由此可得年最高潮位和同期潮差的联合分布为：

F(Z,R)=-

(13)

为进一步检查所选的Frank Copula函数的合理性，对所选函数进行理论联合分布与经验联合分布相关性分析，并对点距进行线性拟合，见图3。

图3 理论联合分布与经验联合分布相关性分析Fig.3 Correlation analysis of theoretical joint distribution and empirical joint distribution

由图3可看出理论联合分布与经验联合分布的相关系数高达0.988 6，且均落在45°线两侧，说明拟合质量较高，所选用的Frank Copula函数是合适的。

2.2 设计组合风险分析

由式(12)分别计算出设计频率50%、20%、10%、5%、2%、1%的高潮位和同期潮差的联合分布概率，由式(10)计算出高潮位和同期潮差的组合风险率见表5。

表5 设计高潮位与同期潮差组合风险率Tab.5 The portfolio risk rate of design high tide andtidal range of corresponding period

由表5可知，镇海潮位站低频率潮位与低频率潮差遭遇的概率极小。其原因在于高潮位的出现是由风暴潮增水引起，增水过程引起高潮位升高的同时也会一定程度上引起低潮位提升，因而潮差不一定会增大。

2.3 设计潮位过程线推求

因为高潮位与潮差的发生不具有同频率的特征，且对防洪标准影响更大的是高潮位，所以潮位过程线的设计应以高潮位设计为主，同时考虑在给定高潮位的条件下，出现几率最大的潮差。由式(12)计算得到年最高潮位相应的条件最可能潮差见表6。

表6 设计高潮位及条件最可能潮差Tab.6 The design high tide level and conditionalmost likely tidal range

由表6可知，镇海站高潮位与条件最可能潮差不具有同频率性，各重现期的高潮位对应的条件最可能潮差均为2～5 a一遇。这种低频高潮位、高频低潮差的组合更不利于河道行洪，容易造成城市洪涝灾害。比如，近5 a的2012年“海葵”、2013年“菲特”、2015年“灿鸿”、“杜鹃”等台风期间的潮位过程均是低频高潮位与高频潮差的组合，对甬江洪水外排造成外海潮位持续顶托作用，导致宁波城市涝水难以外排，造成严重的洪水灾害。

对防洪排涝影响较大的是高潮位，推求设计潮位线首先选定设计高潮位，然后根据表6，按照设计年最高潮位和条件最可能潮差双重控制，等比例缩放典型潮型。以50 a一遇设计潮位过程为例，选取2000年“桑美”台风期间的实测潮位过程作为典型潮型，缩放得到的设计潮位过程见图4。这种方法推求的潮位过程线充分考虑了高潮位和潮差组合的因素，为水利计算提供更合理的下边界，使水利工程设计也更安全。

图4 设计潮位过程Fig.4 Design tidal process

3 结 论

(1)根据优选度评价，选用Frank Copula函数构建镇海站年最高潮位与同期潮差的二维联合分布合理可行。

(2)由设计组合分析可知，镇海潮位站高潮位与潮差遭遇不具有同频率性，低频率高潮位与低频率潮差遭遇的可能性极小。

(3)通过条件最可能组合分析，镇海站各重现期的高潮位对应的条件最可能潮差均为2～5 a一遇。

(4)提出了一种设计高潮位和条件最可能潮差双重控制，等比例缩放典型的方法来推求设计潮位过程线，这样充分考虑的潮差的影响，使工程设计更合理。

□

[1] 杨志勇,袁 喆,方宏阳,等. 基于Copula函数的滦河流域旱涝组合事件概率特征分析[J]. 水利学报,2013,(5):556-561,569.

[2] 张冬冬,鲁 帆,严登华,等. 基于Archimedean Copula函数的洪水多要素联合概率分布研究[J]. 中国农村水利水电,2015,(1):68-74,79.

[3] 李天元,郭生练,刘章君,等. 基于峰量联合分布推求设计洪水[J]. 水利学报,2014,(3):269-276.

[4] 黄锋华,黄本胜,郭 磊,等. 东江干流与支流河涌洪水遭遇风险研究[J]. 中国农村水利水电,2016,(3):144-148.

[5] 茆诗松,濮晓龙,程依明.概率论与数理统计[M].高等教育出版社,2000:331.