电力系统静态电压稳定与节点阻抗解析

侯学勇,鞠 平,史可琴,汤 涌,杨文宇

(1.河海大学能源与电气学院,江苏南京 210098;2.西北电网公司调度中心,陕西西安 710000;3.中国电力科学研究院,北京 100085)

近年来,国内外发生的一系列停电事故,如2003年美国和加拿大的“8.14”事故、2007年我国的“7.1”事故、欧盟的“11.4”事故等,都与电压稳定有关,其严重后果引起了人们的广泛重视.电压稳定问题已成为电力系统研究的重要课题之一,国内外相关的研究非常多,特别是有关静态电压稳定的研究[1-23].

静态电压稳定性是由系统侧和负荷侧两方面共同影响的[5-9],静态电压稳定研究可以从一些关键节点负荷开始.近年来一些基于静态等值的方法被用来研究静态电压稳定性,它们均假设被研究的节点负荷外的系统的等效戴维南参数在某一时刻保持不变,通过辨识等方法跟踪估计从该节点负荷看出去的系统等效戴维南参数[10-18],然后通过各种不同的电压稳定指标来分析系统的电压稳定性[10-11,17,20-21].此类方法均能快速估算出电压稳定裕度,具有概念明确、计算量小的特点.

本文基于简单两节点电力系统,推导出节点负荷最大功率与节点负荷等值阻抗模之间的关系表达式,证明节点最大功率发生的条件是节点负荷等值阻抗模等于电源侧等效阻抗模.给出负荷的最大功率与功率因数之间的关系,以及节点负荷等值阻抗模与节点功率之间的关系,指出以阻抗模作电压稳定判据与节点PV曲线拐点判据之间的联系.分析了传统节点PV曲线下半支的电压稳定性,指出在以比较节点负荷等值阻抗模与临界阻抗模来判别系统电压稳定性时,同样要充分考虑负荷的静态电压特性,如负荷功率水平及负荷组成成分等.

假设节点负荷以外的外部系统可以简化为端口恒定电势的发电机串联一条线路阻抗,那么就可以用发电机-输电线-负荷组成1个简单的电力系统(图1).

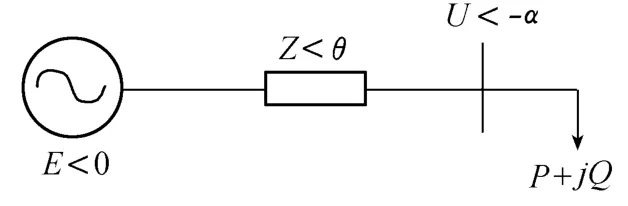
图1 简化电力系统示意图Fig.1 A simplified power system

1 节点最大功率与等值阻抗模[17]

不妨将负荷母线左侧称之为电源侧,右侧称之为负荷侧.根据潮流方程可以获得电源侧方程:

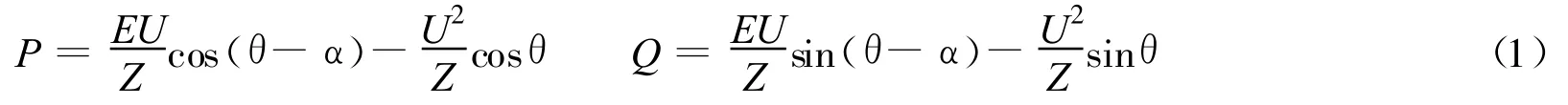
为了表达方便,定义:

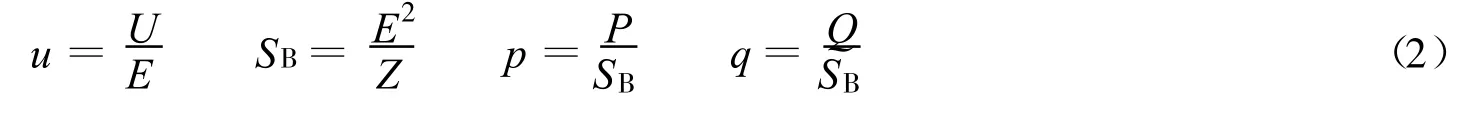
这实际上类似于标幺化,电压的基准值为E,功率的基准值为短路功率SB,一般来说SB很大.则式(1)变为

式(3)中有4个变量,消去其中人们不太感兴趣的角度变量 α,可得描述3个变量之间关系的方程:

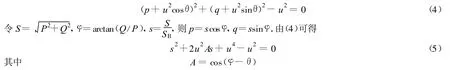
下面求式(5)中s极值点.令可得

根据系统运行特性,取s≥0,u＞0的极值点条件:

此时极值点处电压:

将式(8)代入式(5)消去A,得极值点处功率:

又因ucr=Ucr/E,scr=Scr/SB=ScrZ/E2,则

定义节点负荷等值阻抗模为节点电压模值的平方与其视在功率的比值,即

则由式(10)和(11)可知,ZL=Z,即节点最大功率对应的等值阻抗模等于电源侧等效阻抗模.在上述推导过程中并不涉及负荷模型的问题,即这一结论在任意静态负荷模型下均是成立的.换言之,无论节点负荷组成成分及节点的最大功率随功率因数如何变化,在最大功率处,节点负荷的等值阻抗模总等于电源侧等效阻抗模(下称临界阻抗模).

2 节点负荷最大功率与负荷功率因数

对于相同的电源侧参数(系统的戴维南等效电势和阻抗),节点负荷的最大功率随着功率因数变化而变化,但此时节点负荷的等值阻抗模仍然为电源侧的等效阻抗模.由式(8)和(9)可以画出在给定电源侧参数(E=1.01,=0.02+j0.5,下同)下,节点的最大功率及最大功率处电压(下称临界电压)随功率因数变化的曲线,如图2所示.

由图2可以看出,当节点负荷运行在曲线拐点下方,即在滞后功率因数时,节点的最大功率和临界电压都随着功率因数的增大而增大.而节点负荷通过无功补偿等方式,运行到曲线拐点上方即在超前功率因数时,节点的最大功率和临界电压随超前功率因数的减小而增大.因此,从本质上讲,通过无功补偿的方法能够获得较高的最大功率,但并不意味着就能获得较高的电压稳定裕度,因为系统跟当前的运行点有关[8].

图2 最大功率(Scr)和临界电压(Ucr)随功率因数(cosφ)变化曲线Fig.2 Variation of maximum power Scrand critical voltage Ucr with power factor cosφ

3 节点负荷等值阻抗模与电压稳定

在某一给定功率因数下,负荷的等值阻抗角即为功率因数角,也是固定的,负荷功率随等值阻抗模的变化曲线,可以通过假定节点的负荷为恒阻抗性质,改变节点负荷阻抗模大小并计算其消耗功率得到,图3分别画出了超前和滞后功率因数下的节点负荷功率随阻抗模变化曲线以及节点电压随阻抗模变化的曲线,阻抗模-有功曲线对应的极值点为节点在该功率因数下的临界功率,临界功率处的阻抗值即为临界阻抗模.对比2种不同性质相同功率因数值下的ZL-P和ZL-V曲线,不难发现在相同功率因数的前提下,超前功率因数对应的临界功率要大于滞后功率因数对应的临界功率,且只要给定功率因数值和性质,随着节点负荷阻抗模的减小,节点的电压总是单调减小的.

由图3可以看出,在功率因数恒定下,节点上所挂的负荷可能对应3种情况:(a)与ZL-P曲线有2个交点,这时候系统存在2个平衡点,如图3所示的A和B,节点在这一有功水平下,对应着2个等值阻抗模,它们分别位于临界阻抗模两侧,但它们的阻抗角绝对值是相同的.(b)与ZL-P曲线仅1个交点,系统在这一负荷水平下对应着系统的最大传输功率和临界电压.(c)与ZL-P曲线没有交点,这时候系统不存在平衡点,即在这种负荷水平下电压失去静态稳定.

在静态电压稳定分析中,如果采用恒功率因数增长负荷方式获得节点PV曲线,它实质上对应着某一给定功率因数下系统的一系列平衡点的集合,这可从获得PV曲线的方法上得知.无论是采用常规潮流计算方法还是运用连续潮流计算方法,均假定保持功率因数不变来增长负荷功率以获得PV曲线上的点,从而描绘出PV曲线.而对于两节点系统中节点负荷的PV曲线,本文可以通过式(5)画出s-V的关系曲线.由于功率因数给定,因此很容易得到PV曲线.图4分别给出了超前和滞后功率因数下的系统PV曲线,可以明显看出超前功率因数的最大功率要大于滞后功率因数的最大功率.常规潮流计算方法或连续潮流方法在计算PV曲线上的每一个平衡点时,一般都假定负荷不变,或者说都未考虑负荷的静态电压特性,因此计算出的曲线上每个运行点均只代表了等效电源侧固有的特性,即节点PV曲线的形状仅由给定的负荷功率因数和电源侧的等效参数确定.比较图3和图4可知,PV曲线上同一负荷对应的2个运行点A和B,A点对应着高电压大阻抗,B点对应着低电压低阻抗.以最大功率为分界的PV曲线上下半支,分别对应着以临界阻抗模为分界的负荷等值高阻抗区和低阻抗区,即运行在低阻抗区的节点功率小于临界功率,但与节点静态电压特性是无关的,比如负荷功率水平和组成成分等.

图3 功率因数恒定下的阻抗模-有功和阻抗模-电压曲线Fig.3 Curves of impedance module-power(ZL-P)and impedance module-voltage(ZL-V)under constant power factor

图4 功率因数恒定下的功率-电压曲线Fig.4 P-V curves under constant power factor

当系统给定等效戴维南参数时,分析节点电压稳定性,首先需要判断节点负荷和系统是否存在运行平衡点,然后在运行平衡点处利用各种判据判断系统稳定与否.

3.1 平衡点存在性的讨论

PV曲线上的任意一点,可以看成是曲线自身与节点负荷静态特性曲线的交点.图5画出了4条不同的负荷静态特性曲线a,b,c和d,其中a和b处于同一负荷水平,但它们组成成分不同.a只有恒功率负荷,b包含了40%的恒阻抗和10%的恒电流负荷.c的负荷水平远大于a,但仅包含恒阻抗负荷,b和d负荷组成成分相同,但d的负荷水平远大于b.将它们与PV曲线一并画出,则很容易判断,与本文第3部分中分析类似,节点的负荷静态特性曲线与PV曲线的是否相交也存在3种情形:有2个交点,只有1个交点和没有交点.

3.1.1 有2个交点

也可以分为2类:2个交点分别分布于PV曲线的上下半支上,如图5所示的负荷静态特性曲线a和b与PV曲线相交的情形;另一种是如负荷静态特性曲线c所示,其与PV曲线的2个交点都位于PV曲线的下半支上,此时系统存在2个平衡点.

3.1.2 只有1个交点

图5 节点PV曲线与负荷静态特性曲线Fig.5 P-Vcurve and static load characteristic curves of nodes

图5中将负荷静态特性曲线a或b水平右移均可得到与PV曲线只有1个交点的情形,此时系统仅有1个平衡点,处于临界状态.

3.1.3 没有交点

图5中负荷静态特性曲线d跟系统PV曲线没有交点,此时系统不存在平衡点.

3.2 平衡点稳定性的讨论

在1个平衡点的情况下,系统处于临界电压稳定状态,这很容易理解.而对于3.1中出现的另外2种情况,普遍的观点认为PV曲线上半支上的点是稳定运行点,而下半支上的点是不稳定的平衡点.通过摄动分析,同样是a和c在PV曲线上的交点B,对于负荷静态特性曲线a来说,该平衡点是不稳定平衡点,而对于c来说却是稳定的.因此传统认为在PV曲线下方的运行点就是不稳定的观点是有局限性的.本文认为在负荷成分中含恒阻抗成分较高且负荷水平较高的情况下,在PV曲线下方的部分运行点仍可能是稳定的.因此,在负荷成分中含有较高恒功率且负荷水平低的情况下,PV曲线下方的运行点才是不稳定的平衡点.

3.3 基于阻抗模判据的电压稳定性讨论

一些文献使用节点负荷阻抗模与临界阻抗模的距离来作为电压稳定分析依据,认为节点负荷等值阻抗模大于临界阻抗模时,系统处于电压稳定区域,反之则处于不稳定区域.这实际与根据平衡点在PV曲线上半支或下半支来判断系统电压稳定运行点是一致的,因为由上面分析可知,PV曲线上半支运行点的等值阻抗模大于它的临界阻抗模,PV曲线下半支上的平衡点对应的节点负荷阻抗模小于临界阻抗模.然而由3.2中分析可知,PV曲线的下半支的稳定性还与负荷的静态电压特性有关,因此直接以负荷的等值阻抗小于临界阻抗来判断系统电压不稳定性,这同3.2中一样是具有局限性的.最简单的例子,负荷全部为阻抗型负荷,即使节点负荷阻抗模小于临界阻抗模,系统仍然是电压稳定的,只是此时的节点电压可能处在系统正常运行时的一个不可接受的水平上.由于测量节点的电压和电流来计算节点负荷等值阻抗模时,节点的电压水平通常是可以接受的,此时用阻抗模与临界阻抗模之间距离的判据来估计系统的电压稳定裕度仍然是可行的.

4 结 论

本文根据简单两节点推导出节点的临界功率和临界阻抗模与系统等效戴维南参数的关系,指出无论节点功率因数或节点等值阻抗角如何变化,节点临界功率总是发生在节点负荷等值阻抗模等于电源侧阻抗模的时候.节点的最大功率随着滞后功率因数的增大而增大,随着超前功率因数的增大而减小.随着节点负荷等值阻抗模的减小,节点的电压总是单调减小.指出节点PV曲线下半支上的平衡点对应的节点负荷等值阻抗模总是小于临界阻抗模,而与节点负荷组成成分无关.以节点负荷等值阻抗模与临界阻抗模之间距离来判断系统是否稳定,与用PV曲线下半支判断系统稳定性,同样需要注意负荷的静态电压特性.

[1]IEEE TASK FORCE.Load representation for dynamic performance analysis[J].IEEE Trans on PWRS,1993,8(2):472-482.

[2]IEEE TASK FORCE.Standard load models for power flow and dynamic performance simulation[J].IEEETrans on Power System,1995,10(3):1302-1313.

[3]IEEE Task Force.Bibliography on load models for power flow and dynamic performance simulation[J].IEEE Trans on Power System,1995,10(1):523-538.

[4]CONCORDIA C,IHAR A S.Load representation in power system stability studies[J].IEEE Tran on PAS,1982,101(4):969-977.

[5]TAYLOR C W.Power system voltage stability[M].New York:McGraw-Hill Inc,1994.

[6]CUTSEM T.VAN VOURNAS C D.Voltage stability of electric power systems[M].Boston:Kluwer Academic Publishers,1998.

[7]贺仁睦.电压——无功高级研讨会纪要[J].电力系统自动化,1999,23(9):1-3.(HE Ren-mu.Summary of a workshop on voltage stability and security[J].Automation of Electric Power Systems,1999,23(9):1-3.(in Chinese))

[8]侯学勇,鞠平,陆扬文.电力系统静态电压稳定的三维分析与临界电压[J].河海大学学报:自然科学版,2008,36(3):400-405.(HOU Xue-yong,JU Ping,LU Yang-wen.Three-dimensional analysis of the static voltage stability and the critical voltage in power system[J].Journal of Hohai University:Natural Sciences,2008,36(3):400-405.(in Chinese))

[9]李欣然,贺仁睦,章健,等.负荷特性对电力系统静态电压稳定性的影响及静态电压稳定性广义实用判据[J].中国电机工程学报,1999,19(4):26-30.(LI Xin-ran,HE Ren-mu,ZHANG Jian,et al.Effect of load characteristics on power system stead state voltage stability and the practical criterion of voltage stability[J].Proceedings of the Csee,1999,19(4):26-30.(in Chinese))

[10]李兴源,王秀英.基于静态等值和奇异值分解的快速电压稳定性分析方法[J].中国电机工程学报,2003,23(4):1-4.(LI Xing-yuan,WANG Xiu-ying.Fast voltage stability analysis methods based on static equivalence and singular value resolution[J].Proceedings of the Csee,2003,23(4):1-4.(in Chinese))

[11]VU K,BEGOVIC M M,NOVOSEL D,et al.Use of local measurement to estimate voltage-stability margin[J].IEEE Trans on Power Systems,1999,14(3):1029-1035.

[12]余文杰,方勇杰.一种基于SMARTDevice的低压切负荷算法[J].电力系统自动化,2006,30(21):57-60.(YU Wen-jie.FANG Yong-jie.An undervoltage load shedding method based on SMARTDevice[J].Automation of Electric Power Systems,2006,30(21):57-60.(in Chinese))

[13]王漪,柳焯.基于戴维南等值的系统参数跟踪估计[J].电网技术,2000,24(11):28-30.(WANG Yi,LIU Zhuo.Racking and estimation of system parameter using Thevenin's equivalent[J].Power System Technology,2000,24(11):28-30.(in Chinese))

[14]李娟,刘修宽,曹国臣,等.一种面向节点的电网等值参数跟踪估计方法的研究[J].中国电机工程学报,2003,23(3):30-33.(LI Juan,LIU Xiu-kuan,CAO Guo-cheng,et al.A tracking estimation method for network equivalent parameters of facing the node[J].Proceedings of the Csee,2003,23(3):30-33.(in Chinese))

[15]王芝茗,王漪,徐敬友,等.关键负荷节点集合电网侧戴维南参数预估[J].中国电机工程学报,2002,22(1):16-20.(WANG Zhi-min,WANG Yi,XU Jing-you,et al.Prediction of Thevenin's equivalent parameters on electrical power network side for the muster of key load nodes[J].Proceedings of the Csee,2002,22(1):16-20.(in Chinese))

[16]李来福,于继来,柳焯.戴维南等值跟踪的参数漂移问题研究[J].中国电机工程学报,2005,25(20):1-5.(LI Lai-fu,YU Jilai,LIU Zhuo.Research on parameters drift problem in tracking Thevenin equivalent[J].Proceedings of the Csee,2005,25(20):1-5.(in Chinese))

[17]徐冰亮,柳焯,王永刚,等.电网负荷节点临界阻抗模的性质及意义[J].哈尔滨工业大学学报,1999,31(4):91-95.(XU Bingliang,LIU Zhuo,WANG Yong-gang,et al.The nature and connotation of the critical impedance module of the load bus in power network[J].Journal of Harbin Institute of Technology,1999,31(4):91-95.(in Chinese))

[18]柳焯.基于节点阻抗解析的电压稳定性评估[J].中国电机工程学报,1999,19(11):64-68.(LIU Zhuo.Voltage stability evaluation based on node load impedance analyses[J].Proceedings of the Csee,1999,19(11):64-68.(in Chinese))

[19]柳焯.电压稳定问题中重负荷节点的阻抗解析[J].中国电机工程学报,2000,20(4):35-39.(LIU Zhuo.The impedance analysed of heavy load node in voltage stability studies[J].Proceedings of the Csee,2000,20(4):35-39.(in Chinese))

[20]梁志瑞,于成洋.基于同步相量测量的电力系统等值及电压稳定评估[J].电力科学与工程,2005,21(4):33-36.(LIANG Zhirui,YU Cheng-yang.Power system equivalent and voltage stability evaluation based on synchronized phasor measurement[J].Electric Power Science and Engineering,2005,21(4):33-36.(in Chinese))

[21]段俊东,郭志忠,魏成江.电压稳定临界域的描述及在线近似确定[J].继电器,2007,35(17):47-51.(DUAN Jun-dong,GUO Zhi-zhong,WEI Cheng-jiang.The critical domain description of voltage stability of power system and its dertermination[J].Relay,2007,35(17):47-51.(in Chinese))

[22]梅红伟,钟奇,张金波.有源电力滤波器直流侧电容电压的稳定控制[J].河海大学常州分校学报,2005,19(4):27-29.(MEI Hong-wei,ZHONG Qi,ZHANG Jin-bo.A control method for the stability of the DC bus capacitor voltage of an active power filter[J].Journal of Hohai University Changzhou,2005,19(4):27-29.(in Chinese))

[23]黄建新,洪佩孙,索丽生.新型静止无功发生器(ASVG)的模糊控制研究[J].河海大学学报:自然科学版,1998,26(3):81-86.(HUANG Jian-xin,HONG Pei-sun,SUO Li-sheng.Study of ASVG control by using a fuzzy controller with auto tuned scaling factors[J].Journal of Hohai University:Natural Sciences,1998,26(3):81-86.(in Chinese))