偏最小二乘法与人工神经网络耦合的小流域产沙模型

李世欣,温 建,邵孝侯,王晓亚,王玉英

(1.河海大学水利水电学院,江苏南京 210098;2.河南农业大学机电工程学院,河南郑州 450002;3.河南农业大学信息与管理科学学院,河南郑州 450002;4.河南省南召县水土保持科学研究站,河南 南召 474650)

水土流失是当今世界人们普遍关注的重大生态问题之一,已成为我国首要的和最大的环境问题[1].目前,我国土壤侵蚀面积(包括水蚀、风蚀和冻融蚀面积)达484.74万km2,占全国国土面积的51.1%[2],土壤侵蚀的加剧是造成土地荒漠化、洪涝灾害、水土资源危机的主要原因之一.多年来,国内外学者对土壤侵蚀的机理和规律进行了系统研究,并从不同角度、采用不同理论、利用不同影响因子建立了适应于不同地域特征的土壤侵蚀模型,有效指导了土壤侵蚀的预防和治理工作.尤其是近20多年来,随着应用数学和信息技术的不断发展,一些新的技术理论被应用到土壤侵蚀规律及应用模型的研究中,如分形理论[3]、人工神经网络[4]、RS和GIS技术[5]等,拓宽了土壤侵蚀的研究思路,提高了土壤侵蚀模型的预测精度.

偏最小二乘回归(partial least-squares regression,PLSR)是一种新型多元统计数据分析法.该方法集多元线性回归分析、典型相关分析和主成分分析的基本功能于一体,通过在变量系统中提取若干个对系统具有最佳解释功能的综合信息变量,实现对高维数据空间的降维处理.该方法有效解决了自变量间存在严重多重相关性以及样本点个数较少等建模问题.人工神经网络(artificial neural network,ANN)具有模拟人类大脑思维功能的能力,理论上可以实现任意函数的逼近,达到人们希望的精度要求.本文将偏最小二乘回归(PLSR)与神经网络(ANN)结合,建立了偏最小二乘神经网络耦合模型(PLS-ANN),并应用于小流域侵蚀产沙预报.

1 偏最小二乘神经网络模型的构建方法

1.1 偏最小二乘回归模型(PLSR模型)[6-8]

设有因变量集合Y={y1,y2,…,yq}n×q和自变量集合X={x1,x2,…,xp}n×p,偏最小二乘回归分别在X,Y中提取主成分t1和u1,并要求:(a)t1和u1尽可能多地携带它们各自数据表中的变异信息,尽可能好地代表X和Y;(b)t1和u1的相关程度能够达到最大,t1对u1有最强的解释能力.

在第1成分t1和u1被提取后,偏最小二乘回归分别实施X对t1的回归和Y对t1的回归.如果回归方程已经达到满意精度,则算法终止;否则,将X被t1解释后的残余信息和Y被u1解释后的残余信息进行第2轮的成分提取,如此往复,直到达到一个较为满意的精度为止.若提取了h个主成分t1,t2,…,th,则这h个主成分即为从原数据信息中提取的综合变量.这些变量对系统的解释性最强,并克服了自变量之间的多重相关性,剔除了噪音信息的干扰.

方程精度可采取交叉有效性原则进行检验.在偏最小二乘回归建模中,究竟应选取多少个成分为宜,一般采用交叉有效性原则进行判别[9-10]:除去某个样本i的所有集合并使用h个成分拟合一个回归方程,把排除的样本点i代入前面的回归方程,得到yi在样本点i上的拟合值对每一个样本点重复上述计算,定义yi的预测误差平方和为Phj,则有记Y的预测误差平方和为Ph,则.变量Ph取最小值时表明模型的拟合效果最好,这时提取的成分个数h即为最佳成分数.

当q=1时,则上述问题由多因变量PLSR模型转变为单因变量的PLSR模型,它是多因变量PLSR模型的一种特例,小流域侵蚀产沙研究的即为单因变量问题.

1.2 偏最小二乘神经网络模型(PLS-ANN)[8-11]

人工神经网络系统具有大规模的并行处理和分布式信息存储能力,能自动调整内部神经元之间的连接权重,以匹配输入输出响应关系,具有良好的自组织性和学习功能.本文选取典型的3层前馈型BP(back propagation)网络模型[4,12].BP网络模型通常由输入层、隐含层和输出层构成.PLS-ANN模型构建方法为:用偏最小二乘(PLS)方法提取的h个主成分t1,t2,…,th作为BP模型的输入,输出层为1个节点y,隐含层传输函数选择sigmoid函数,隐含层节点数的确定采用试错法,经多次调试选择最佳节点个数,模型结构如图1所示.

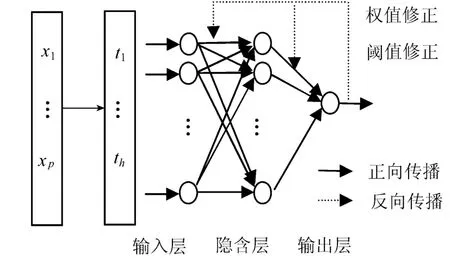
图1 PLS-ANN模型结构Fig.1 Structure of PLS-ANN model

2 小流域侵蚀产沙的PLS-ANN模型

2.1 研究区概况

和平沟小流域位于河南省南召县西部,北纬 112°15′～ 112°18′,东经 33°17′～ 33°20′之间,面积 9.62km2,地质岩性为斑状花岗岩,土壤类型主要为沙壤和黄棕壤.多年平均降雨量1020mm,年均气温14.8℃.流域上宽下窄,为一扇形闭合集水单元,林草覆盖率88%,海拔高程236～919m.

南召县水土保持科学实验站在流域内设3个基本雨量站,均设雨量计测定降雨量;在小流域下游设总控制断面,测定径流和泥沙.

2.2 数据及方案

影响流域侵蚀产沙的因素主要有地质地貌、土壤类型、降雨径流、植被状况等自然因素和人为因素.对一个小流域而言,一定时期内地质地貌、土壤类型等下垫面因素对小流域产流、产沙的影响是相对稳定的,降雨成为影响流域侵蚀产沙的直接动力因子,而只有产生径流的降雨才能产生侵蚀,因此降雨因子和径流因子是侵蚀产沙的重要影响因子[13-14].林草植被对侵蚀产沙有一定的减缓作用,是影响土壤侵蚀的关键因子[15],输沙率是水文泥沙监测的重要指标,与输沙量关系密切.事实上,小流域内降雨、土壤、地形、植被、人类活动相互作用结果最终都体现在流域出口处,在洪水和泥沙等特征中表现出来[16].所以本文采用1984～2006年南召县水保站的实测资料,选取流域年降水量x1、年产流雨量x2、年降水日数x3、年径流深x4、年最大1日径流量x5、年最大流量x6、林草覆盖率x7、年最大1日平均输沙率x8等8个因子作为自变量,年输沙量y作为因变量.为了评价PLS-ANN模型的效果,分别采用PLSR模型、BP神经网络模型和PLS-ANN模型进行计算,并对计算结果进行了比较.

2.3 结果与分析

利用前1984～2002年的数据建立产沙模型,2003～2006年的数据用于模型检验.首先,利用偏最小二乘方法对8个自变量进行成分提取.根据交叉有效性原则,提取的3个成分为最佳成分,见图2.

3个主成分t1,t2,t3表达式为

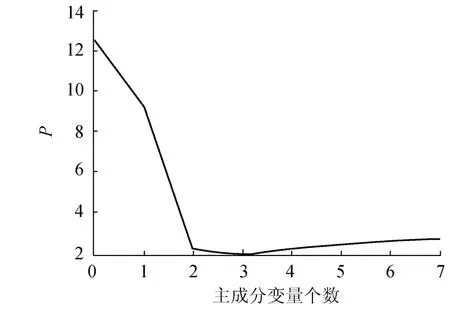
图2 PRESS相对于所取成分数的变化Fig.2 Variation of PRESS against number of components extracted from PLS model

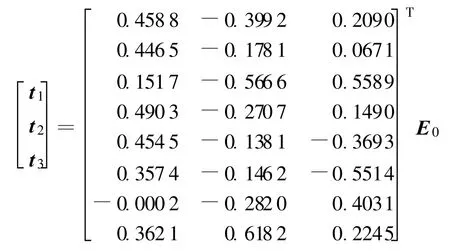
其中E0为原始数据X([x1,x2,…,x8]19×8)标准差标准化处理后的矩阵.采用下式进行标准差标准化,即

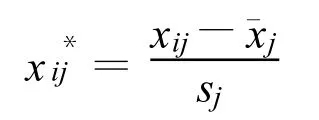
式中:xij——矩阵X的第i行第j列元素的值;sj,——矩阵X第j个自变量的标准差和平均值;的标准化值.将偏最小二乘法提取的3个主成分t1,t2,t3作为神经网络的输入,y作为输出,设定精度为0.0001,进行学习训练,训练1368次就可满足精度要求.若将8个自变量作为输入样本,直接输入BP神经网络,同样的精度要求则需要训练6841次方可收敛.

a.拟合误差分析.分别用PLS-ANN模型、BP神经网络模型和PLSR模型建立产沙模型,对1984～2002年的产沙量进行拟合,并将拟合值与观测值进行比较(图3).

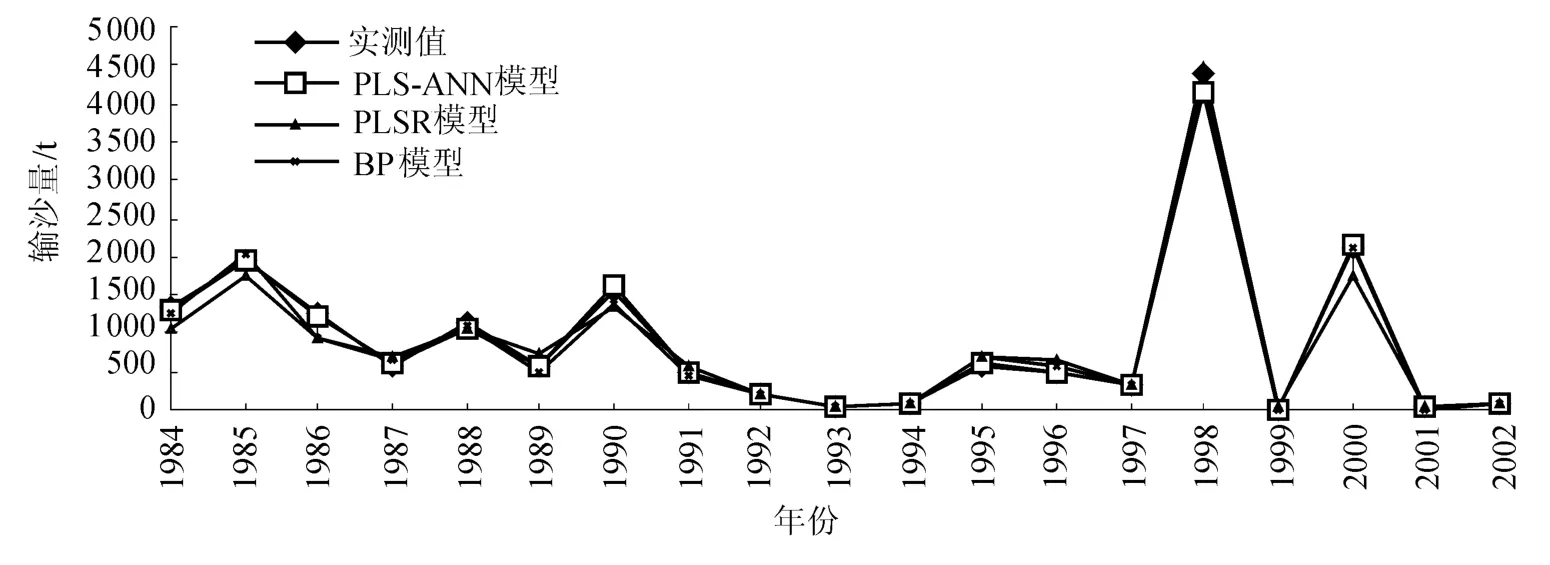
图3 小流域产沙量拟合精度比较Fig.3 Comparison of fitting precision for sediment yield in small watershed

PLSR模型拟合误差平均为18.66%,误差在10%以下的年份有6个,误差大于50%的年份有1个;BP神经网络的模型误差稍低,平均值为13.99%,误差为10%以下的年份有7个,误差大于50%的年份没有;PLSANN模型误差最小,平均值达到6.57%,仅有3个年份的模拟误差大于10%,最高为19.92%,其余年份的误差均在10%以下.

b.检验误差分析.应用所建立的PLS-ANN模型对2003～2006的数据进行检验,并与PLSR模型和BP神经网络模型进行比较(表1).由表1可看出:BP网络模型有1个年份的误差高达27.70%,其中有2个年份的误差均在10%以下,平均误差为14.11%;PLSR模型有2个年份的误差在20%以上,2个年份的误差在10%以下,平均误差为20.33%,最大误差为25.27%;PLS-ANN模型误差均在20%以下,最大误差为16.08%,有3个年份的误差均在10%以下,平均误差仅为7.5%.可见,无论是拟合还是检验的精度,偏最小二乘神经网络模型都比单一方法高.

表1 检验结果对比Table 1 Comparison among test results of different models

3 结 语

a.流域侵蚀产沙是一个复杂的自然过程,受自然因素、人为因素等诸多因素影响.本文选取8个自变量,采取PLS方法提取的主成分,不仅携带更多的自变量信息,而且对因变量影响程度最大.本文所建立的PLS-ANN模型,既解决了自变量之间相关性和样本数据较少的问题,又降低了神经网络的输入维数,加快了网络收敛速度,增强了网络稳定性,降低了模型的模拟误差和检验误差.

b.PLS-ANN模型拟合误差平均为6.57%,检验误差平均为7.5%,均比PLSR模型和BP网络模型要低,表明对复杂的非线性小流域产沙系统,PLS-ANN模型能更好地反映其本质特征.

c.PLS-ANN模型选取的自变量均为容易获取或测定数据,模型计算方便,实用性较强,对研究豫西南山区水土流失规律和支持当地生态环境建设具有一定实用价值.

[1]郑粉莉,王占礼,杨勤科.我国土壤侵蚀科学回顾和展望[J].自然杂志,2008,30(1):12-16.(ZHENG Fen-1i,WANG Zhan-li,YANG Qin-ke.The Retrospection and prospect on soil erosion research in China[J].Chinese Journal of Nature,2008,30(1):12-16.(in Chinese))

[2]李智广,曹炜,刘秉正,等.我国水土流失状况与发展趋势研究[J].中国水土保持科学,2008,6(1):57-62.(LI Zhi-guang,CAO Wei,LIU Bing-zheng,et al.Current status and developing trend of soil erosion in China[J].Science of Soil and Water Conservation,2008,6(1):57-62.(in Chinese))

[3]崔灵周,李占斌,郭彦彪,等.基于分形信息维数的流域地貌形态与侵蚀产沙关系[J].土壤学报,2007,44(2):197-203.(CUI Ling-zhou,LI Zhan-bin,GUO Yan-biao,et al.Fractal-information-dimension-based relationship between sediment yield and topographic feature of watershed[J].Acta Pedologica Sinica,2007,44(2):197-203.(in Chinese))

[4]赵西宁,王万忠,吴普特,等.坡面入渗的人工神经网络模型研究[J].农业工程学报,2004,20(3):48-50.(ZHAO Xi-ning,WANG Wan-zhong,WU Pu-te,et al.Artificial neural networkmodel for soil infiltration in slope farmland[J].Transactionsof the Chinese Society of Agricultural Engineering,2004,20(3):48-50.(in Chinese))

[5]马修军,谢昆青.GIS环境下流域降雨侵蚀动态模拟研究:以PCRaster系统和LISEM模型为例[J].环境科学进展,1998,7(5):137-144.(MA Xiu-jun,XIE Qun-qing.Dynamic simulation of rainfall erosivity by GIS:based on the system of PCRaster and the model of LISEM[J].Advances in Environmental Science,1998,7(5):137-144.(in Chinese))

[6]付强.数据处理方法及其农业应用[M].北京:科学出版社,2006:164-204.

[7]WOLD S,TRYGG J,BERGLUND A,et a1.Some recent developments in PLS modeling[J].Chemometrics and Intelligent Laboratory Systems,2001,58:13l-150.

[8]陈南祥,黄强,曹连海.基于偏最小二乘回归与神经网络耦合的岩溶泉预报模型[J].水利学报,2004(9):68-72.(CHEN Nanxiang,HUANG Qiang,CAO Lian-hai.Model for prediction of karst spring flow based on the coupling of neural network modelwith partial least square method[J].Journal of Hydraulic Engineering,2004(9):68-72.(in Chinese))

[9]EFRON B,GONG G.A leisurely book at the bootstrap,the jackknife and cross validation[J].The American Statistician,1983,37(1):36-48.

[10]曾九孙,刘祥官,罗世华,等.主成分回归和偏最小二乘法在高炉冶炼中的应用[J].浙江大学学报:理学版,2009,36(1):33-36.(ZENG Jiu-sun,LIU Xiang-guan,LUO Shi-hua,et al.Application of principal component regression and partial least square in blast furnace iron-making[J].Journal of Zhejiang University:Science Edition,2009,36(1):33-36.(in Chinese))

[11]戈汉权,施泽进,任在清.基于偏最小二乘与神经网络耦合的储层参数预测[J].成都理工大学学报:自然科学版,2007,34(6):618-620.(GE Han-quan,SHI Ze-jin,REN Zai-qing.Prediction of the reservoir parameters based on the coupling of neural network model with partial least square method[J].Journal of Chengdu University of Technology:Sci&Technol Ed,2007,34(6):618-620.(in Chinese))

[12]朱大奇,史慧.人工神经网络原理及应用[M].北京:科学出版社,2006:36-63.

[13]许全喜.人工神经网络模型在流域水沙预报中的应用[J].人民长江,2000,31(5):30-32.(XU Quan-xi.Application of artificial neural network in predicting soil erosion[J].Yangtze River,2000,31(5):30-32.(in Chinese))

[14]蔡强国,刘纪根,刘前进.岔巴沟流域次暴雨产沙统计模型[J].地理研究,2004,23(4):433-439.(CAI Qiang-guo,LIU Ji-gen,LIU Qian-jin.Research of sediment yield statistical model for single rainstorm in Chabagou drainage basin[J].Geographical Research,2004,23(4):433-439.(in Chinese))

[15]张志强,王盛萍,孙阁,等.流域径流泥沙对多尺度植被变化响应研究进展[J].生态学报,2006,26(7):2356-2364.(ZHANGZhi-qiang,WANG Sheng-ping,SUN Ge,et al.Runoff and sediment yield response to vegetation change at multiple scales:a review[J].Acta Ecologica Sinica,2006,26(7):2356-2364.(in Chinese))

[16]侯建才,李占斌,李勉,等.流域次降雨侵蚀产沙的BP神经网络模拟[J].水土保持通报,2007,27(3):79-83.(HOU Jian-cai,LI Zhan-bin,LI Mian,et al.Back propagition neural network simulation on sediment yield of watershed under single rainfall[J].Bulletin of Soil and Water Conservation,2007,27(3):79-83.(in Chinese))