k-kl模型在风生混合流中的应用

张 卓,宋志尧,孔 俊,张 凤

(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.南京师范大学虚拟地理环境教育部重点试验室,江苏南京 210097)

紊流模型发展于20世纪70年代,当时主要用于气体动力研究中,近十多年来,包括k-kl,k-ε模型开始在海洋工程中得到广泛应用.

k-kl模型是在海洋工程中较为常用的双方程紊流模型,在模拟大气海洋边界层及全球环流方面有较强的优越性[1].自从首个k-kl模型Meller-Yamada(MY)模型于20世纪末在河口、近海及海洋领域得到广泛使用以来[2],k-kl模型开始被许多学者关注并且提出了各自的改进方法,包括对双方程(主要是kl方程)系数的调整,壁函数的改进[3],压强应变项封闭模型的改进[4]等,这些改进方法都在各自的应用领域内取得了令人满意的结果,但缺乏同一种情况下进行多因素综合比较的例子,这就给k-kl模型在实际工程中的应用带来了不便.因此,本文主要考虑在风生混合流情形下,不同方法对紊流模型模拟结果的影响,为在实际类似情形下,如河口的盐水入侵,污染物迁移等情况下,合理地选取、调整和改进k-kl模型提供参考和借鉴.

1 k-kl模型

k-kl模型以紊动能k和紊动能通量kl建立对流扩散方程:

式中:νt——垂向紊动系数;u——流速矢量;P,B,ε——紊动能产生项、浮力项和紊动耗散项;Fwall——壁函数;σk,σl,c1,c2,c3——常数,分别取1.96,1.96,0.9,0.5,其中c3的取值和稳定函数以及稳态里查德森数关联;t,z——时间和垂向坐标.

底面边界条件和表面边界条件一般采用对数层边界,即

式中:u*——摩阻流速;cμ 0——稳定函数在对数层下的常值;κ——卡门常数,取0.4.

由式(1)～(4)可以数值求解得到k和kl的分布,再通过式(5),(6)便可以得到垂向紊动系数和垂向扩散系数的分布,最后可以利用这些系数来求解N-S方程及温度扩散方程.

式中 :cμ,c′μ——稳定函数 ;l——紊动尺度 ;ν′t——垂向扩散系数.

通过众多文献中k-kl模型的比较[5-7],发现这些模型主要有3个方面不同:(a)稳定函数cμ.从式(5),(6)可以看到,cμ大小直接影响扩散系数的分布.(b)壁函数Fwall.作为kl对流扩散方程中源项的一部分,会对kl的分布产生影响.(c)式(2)中的c3取值.在对c1和c2取值大同小异的情况下,对同一种稳定函数c3的取值其实由稳态里查德森数Rist唯一确定.

2 算例简介

Kato等[8]曾通过风生密度混合流试验来研究混合层的变化情况.在试验中,由常数风应力作用在稳定分层的水流表面,引起混合层自上而下逐渐发展.水深取得较大,因此可以忽略底面边界层的影响,看成无限水深的情况.Prince[9]根据Kato等的试验数据,总结了经验公式:

式中:Dm——混合层深度;u*s——表面摩阻流速,在试验中取10-2m/s;t——施加风应力的时间.

本文的数学模型根据Kato等的试验建立,水流模型采用ELCIRC斜压模型[10],计算区域为5000m×100m,深度为50m,水平网格尺度为100m×20m,南北闭边界,东西采用定水位开边界,水流可自由出入.垂向网格采用自下而上逐渐加密的方式,总共分50层.底面阻力设0以消除底面边界层的影响.初始表面温度12.5℃,底面温度10℃,相应的;数模中混合层深度采用文献[11]的定义,即从水面开始向下所有k＞10-5m2/s2的区域都看作混合层.其余参数如下:网格结点96,单元数75,表面切应力τs=0.1Pa,时间步长120s,参考密度 ρ0=1000kg/m3.

3 结果分析

3.1 稳定函数的影响

海洋数值模型必须考虑水流的斜压及分层效应,通常河道中将cμ直接等于cμ 0的方法显然已不能满足需要,因此从Meller开始,陆续提出了MY,KC,LD,CA,CB,CH等6种稳定函数,其中CA,CB,CH都是2000年后提出的.这6种稳定函数都是在雷诺应力方程中简化而来,差异主要源于对压强应变相关量的不同封闭模型.而Burchard等[11-12]将这6种稳定函数表达成统一的形式,在准平衡态下,又可表达为理查德森数Ri的函数:

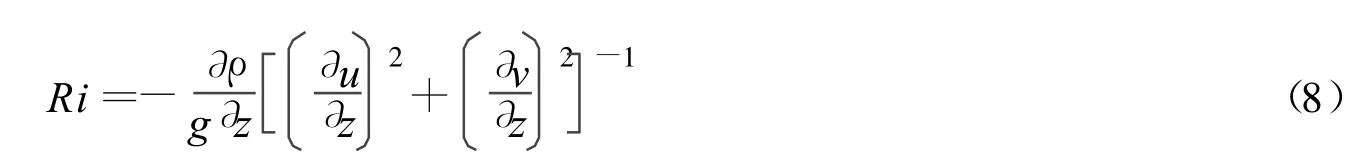
将6种稳定函数的曲线绘制于图1.

本文关心的主要是稳定分层区域即Ri＞0.可以看到,随着Ri的增大,cμ和c′μ减小,表示了分层作用越强或剪切作用越弱,垂向扩散会因此得到削弱的物理机制.稳定函数对垂向紊动扩散系数的影响体现在2个方面:一是直接体现在计算中,如式(5)和(6);二是通过影响c3的取值从而决定kl的分布.将壁函数统一取抛物改进型,稳态里查德森数Rist取0.19.图2表示6种稳定函数的混合层边界位置随时间变化关系.可以看到,MY,KC,LD的结果比较接近,三者之中以KC的结果最接近经验公式(7),但三者得到的混合层扩散速率都显得快了些,CA,CB,CH的结果比较接近,总体来讲,好于MY,KC,LD,这主要是因为CA,CB,CH在压强应变项中加入了浮力项、各项异性产生项以及涡重分布项,考虑因素更全面的缘故.

3.2 壁函数的影响

在近壁区域,水流处于对数层区,忽略浮力项且P=ε,则式(2)可转化为

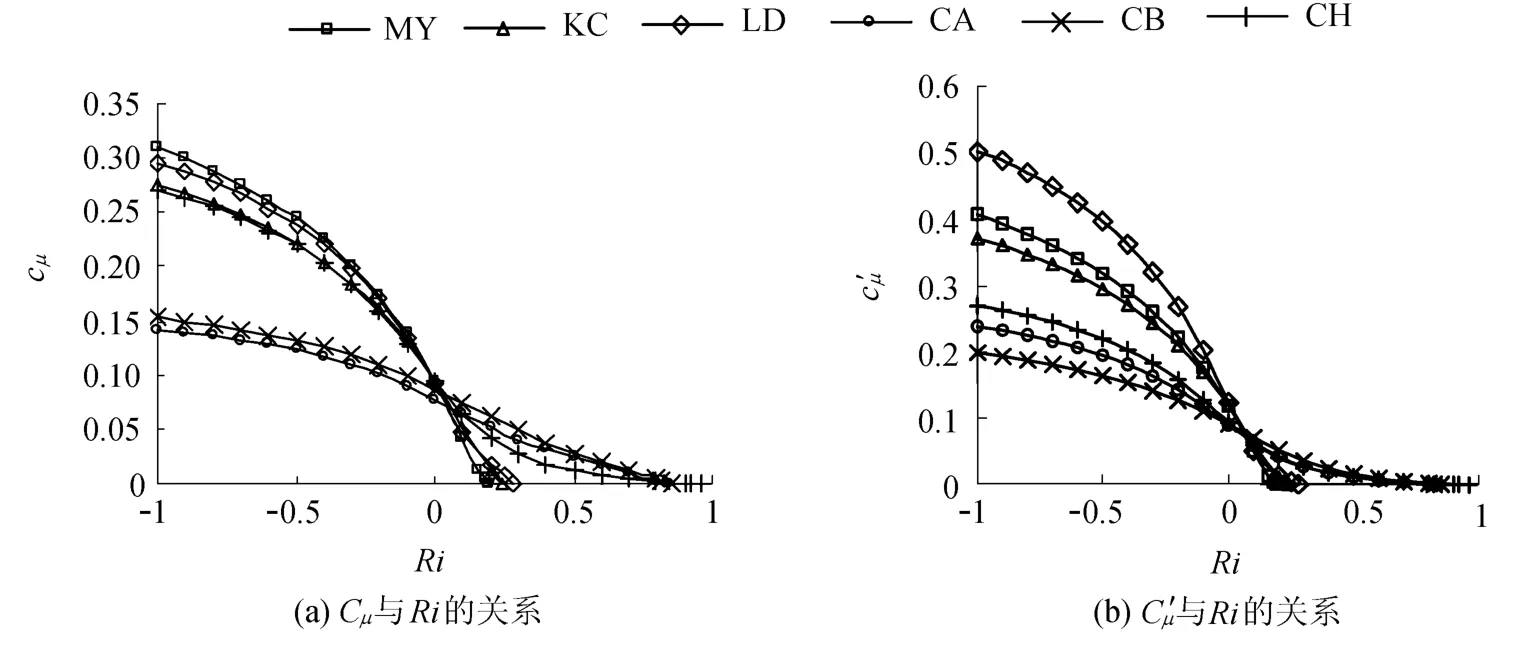
图1 准平衡状态下6种稳定函数和Ri的关系Fig.1 Relationship between 6 kinds of stability functions and Richardson number Ri under quasi-equilibrium condition

其中 ε=c3μ0k3/2l-1,νt可以通过式(5)得到,只是对数层下cμ=cμ0,并将k近似为常数,代入式(9),整理后得

如果l=κz,那么可以得到 σl的表达式

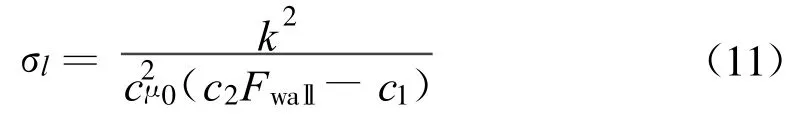
可以看到要使 σl始终为正,必须使c2Fwall＞c1.

比较常用的壁函数有3种[3]:

式中卡门常数k=0.4,db和ds分别是距离底面和表面的长度.

稳定函数采用CH模型,稳态里查德森数取0.25,得到3种壁函数条件下的混合层边界位置随时间变化曲线(图3).可以看到,抛物改进型较抛物线型和对称型的混合层扩散速率小一些,更接近于经验公式,这主要是因为抛物改进型较抛物线型的值在边界附近相对较小,σl的值较大,kl的扩散速率下降的缘故.

图2 不同稳定函数混合层边界位置随时间变化关系(水面在50m处)Fig.2 Development of mixed layer depth under different stability functions(water level at a depth of 50m)

3.3 稳态里查德森数Rist的影响

考虑平衡时状况,即紊动产生等于耗散,将式(1),(2)简化后,代入耗散项与紊动尺度之间的关系

结合式(5),(6)可推导出c3和里查德森数Ri存在如下对应关系

准平衡态下,稳定函数可表达为理查德森数Ri的函数,c3仅由Ri确定.此时的式(1),(2)都处于平衡态,Ri称为稳态里查德森数,用Rist表示.试验表明,Rist的值在0.2～0.25之间.这就意味c3的取值不仅仅要使结果和经验公式(7)吻合,而且要使Rist的取值在合理范围,否则便失去了模型本身的物理意义[6].在这点上,MY模型显然有不足(Rist最大只能取到0.1939),图4表示CH模型在不同Rist下的混合层扩散曲线.从图4可以看到,增加Rist会增大同时刻的混合层深度,也就是使垂向紊动加强.为分析产生这种情况的原因,可以首先看某个时刻水层中Ri的分布.表层动量显然最大,然后向下递减,因此Ri在表层最小,然后向下逐层增大,一直增大到Rist,此时紊动能k的产生和耗散正好达到平衡,k即保持常数值.再往下,随着混掺长度的增加,k的耗散大于产生,紊动逐渐减小,直至消失(消失是指风应力产生的垂向紊动小到某个界限下,如10-5,水体本身的紊动依然存在.对于一个较小的Rist,Ri很快就能达到,因此紊动很早就被抑制;而一个相对较大的Rist,必须在更深的水层中才能达到,所以紊动也要在更深层才被抑制.

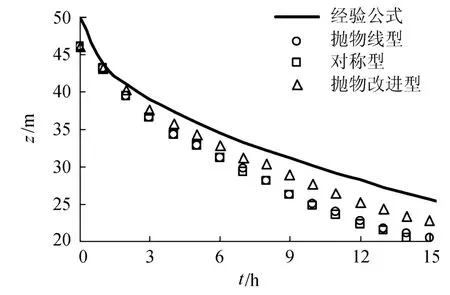
图3 不同壁函数混合层边界位置随时间变化关系(水面在50m处)Fig.3 Development of mixed layer depth under different wall functions(water level at a depth of 50m)

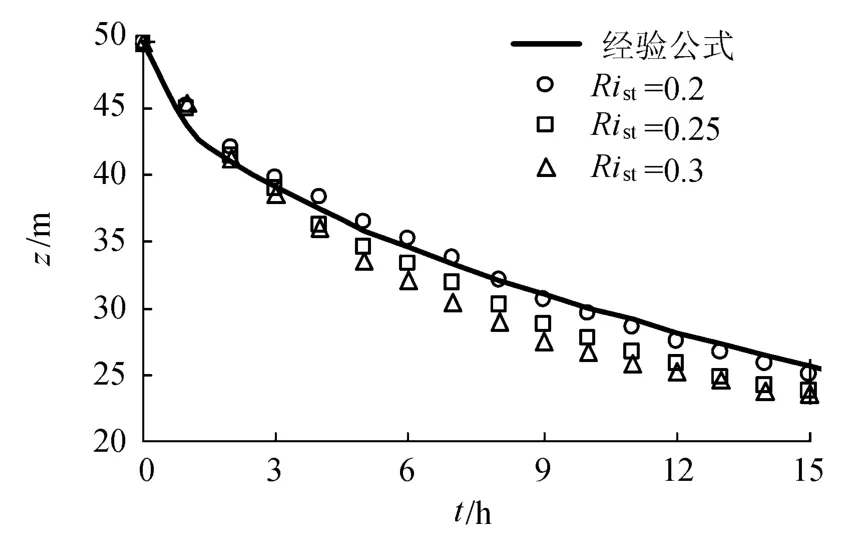
图4 不同 Rist下混合层边界位置随时间变化关系(水面在50m处)Fig.4 Development of mixed layer depth under different Rist(water level at a depth of 50m)

4 结 语

a.稳定函数的选择会影响k-kl模型的计算结果,这种影响不仅体现在计算紊动扩散系数中,而且还体现在对kl分布的影响上,比较而言CA,CB,CH的结果稍好于MY,KC,LD.

b.壁函数采用抛物改进型能使结果更接近实际,而对称型和抛物线型壁函数都高估了边界附近kl的扩散速率.

c.对同一种稳定函数而言,如果k-kl又采用了同一种壁函数,那么影响混合层的主要是Rist.当Rist增大时,混合层也会加快发展,这是由Rist本身的性质决定的.

[1]范聪慧.多因素对海洋上混合层深度影响的数值模拟[D].北京:中国科学院,2007.

[2]MELLER G L,YAMADA T.Development of a turbulence closure models for geophysical fluid problems[J].Review of Geophysics,1982,20:851-875.

[3]WARNER J C,SHERWOOD C R.Performance of four turbulence closure models implemented using a generic length scale method[J].Ocean Modelling,2005,8:81-113.

[4]CANUTO V M,HOWARD A,CHENG Y,et al.Ocean turbulenceⅠ:one-point closure model:momentum and heat vertical diffusivities[J].J Phys Oceanogr,2001,31:1413-1426.

[5]GALPERIN B,KANTHA H,HASSID S.A equasi-equilibrum turbulent energy model for geophysical flows[J].J AtmosSci,1988,45:55-62.

[6]龚政.长江口三维斜压流场及盐度场数值模拟[D].南京:河海大学,2002.

[7]BURCHARD H,PETERSON O.Models of turbulence in the marine environment:a comparative study of two-equation turbulence models[J].JMar Syst,1999,21:29-53.

[8]KATO H,PHILLIPS O M.On the penetration of a turbulent layer into stratified fluid[J].J Fluid Mech,1969,37:643-655.

[9]PRICE J E.On the scaling of stress-driven entrainment experiment[J].J FluidMech,1979,90:509-529.

[10]ZHANG Y,BAPTISTA A M.A cross-scale model for 3D baroclinic circulation in estuary-plume-shelf systems:Ⅰ:formulation and skill assessment[J].Continental Shelf Research,2005,25:935-972.

[11]UMLAUF L,BURCHARD H.Second-order turbulence closure model for geophysical boundary layers:a review of recent work[J].Continental Shelf Research,2005,25:795-827.

[12]CHENG Y,CANUTO V M,HOWARD A M.An improved model for the turbulent PBL[J].Journal of the Atmospheric Sciences,2002,59:1550-1565.