电力变压器全斜接缝叠片铁心工作条件下的磁性能模拟
杜 永 程志光 颜威利 范亚娜 张俊杰 刘兰荣
(1. 河北工业大学电气与自动化学院 天津 300130 2. 保定天威集团技术中心 保定 071056)
1 引言
大型电力变压器中的铁心和磁屏蔽采用高导磁性能的取向硅钢片叠积而成,对叠片铁心和磁屏蔽中的杂散损耗、局部过热问题的分析及其结构优化是电力变压器设计中的重点问题,特别在特高压、特大容量电力变压器研发中倍受关注。为了研究包括铁心和屏蔽在内的大型电力变压器构件中的杂散损耗问题的分析方法和严格检验其工程有效性,作者提出并经持续扩展建立了国际 TEAM(Testing Electromagnetic Analysis Methods)21基准族,对此进行了系统的数值仿真和实验研究[1-2]。大量的研究结果表明,不论是磁性材料中的电磁场分布,还是损耗分布,其结果的准确度和有效性归根结底还是取决于材料在其实际工作状态下的电磁性能[3-4]。而电工材料供应商提供的电磁性能数据通常是在标准规定的条件下测量得出的。例如采用传统的爱泼斯坦方圈以及单片测量仪的测量条件(包括供电电源、环境温度等)和试件取样均有严格规定。但这种标准条件下测量得到的数据并不能完全反映实际工况下变压器铁心叠片材料的真实性能,有些性能数据如铁心接缝处的励磁伏安等,硅钢片供应商一般也无法提供。由于铁心叠片材料磁性能数据的不充分,导致了对叠片铁心的磁场和损耗的分布难于进行精确的计算和分析[5]。
在单个铁心模型上确定其几何平均磁路长度,通过测量铁心损耗的无功分量和有功分量,可得到铁心总的励磁伏安和有功铁损。但是,这种简单的基于几何平均磁路长度的测定方法得到的性能数据并不准确[6]。P. Marketos,S.Zurek和 A. J. Moses通过基于爱泼斯坦方圈法进一步的研究表明,采用IEC标准规定的等效磁路长度没有充分考虑试样搭接区域对磁路长度变化的影响,需要对等效磁路长度进行更加精确的测量和计算[7]。
本文提出使用两个完全按照电力变压器铁心的标准设计和叠装工艺制作的产品级模型[8],采用双铁心法模拟叠片铁心材料的磁性能,包括等效磁路长度的确定,以及铁心“接缝区”和“柱轭区”的励磁伏安特性的分离等。本文建立的工业模型更接近电力变压器的铁心,可获得具有工程意义的数据。但与爱泼斯坦方圈相比在尺寸、接缝型式、线圈的配置、空气补偿等均有不同。
2 双铁心模型及其参数
两个产品级的铁心模型全部采用 45°全斜接缝、每级两片、三级步进、5mm搭接的叠装工艺制作而成。Model C1和Model C2,两模型,在“接缝区”的型式和结构尺寸完全相同,不同的只是“柱轭区”的长度。模型具体参数如图1和下表所示。

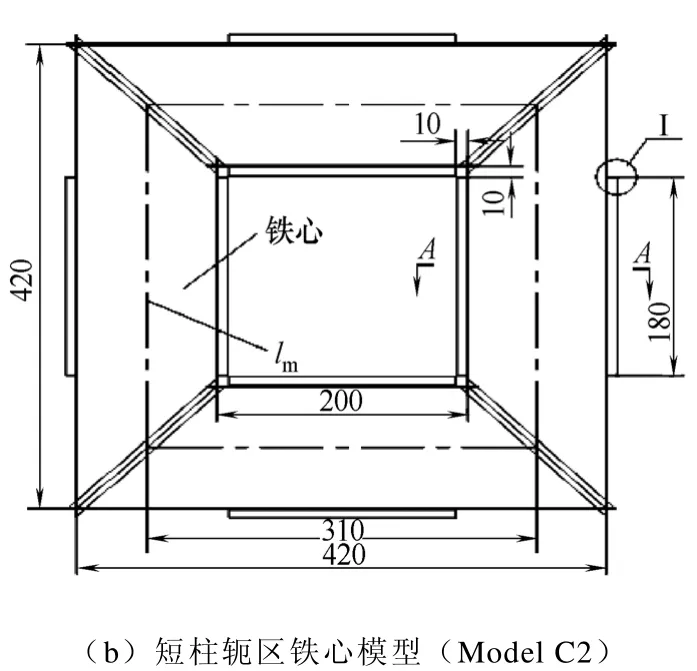
图1 双铁心模型示意图Fig.1 Two laminated core models

表 模型参数Tab. Parameters of the models
3 模型等效磁路长度及接缝影响域
磁路长度的确定在材料的磁特性测量中具有重要意义。例如,在标准的 25cm爱泼斯坦方圈测量法中,不取用几何平均磁路长度(1m),而是采用IEC标准规定的等效磁路长度(0.94m),用于测量结果处理[9]。显然,不是在任何情况下如此规定的等效磁路长度都合理。
本文采用两个方形铁心模型确定铁心的等效磁路长度,在测量磁化曲线以及进行铁心“接缝区”和“柱轭区”的励磁伏安分离时使用。
参照国家标准[9],导出铁心模型的等效磁路长度的计算公式。根据国家标准中的定义,模型等效质量me的计算如式(1)所示。

式中 m——模型总质量,单位kg;
Le——模型等效磁路长度,单位m;
Lm——模型几何平均磁路长度,单位m。
改写式(1),即可得出模型的等效磁路长度

显然,一旦完成铁心模型的设计和研制,则模型的总质量 m和几何平均磁路长度 Lm就已知。在式(2)中,只需要确定出模型的等效质量 me就可以计算出模型的等效磁路长度Le。
本文中模型的等效质量 me是根据功率测量结果得出的。图2中阴影区域表征两个模型的柱轭长度之差,假定其中的磁场分布和损耗分布是均匀的。通过测量和计算得出该区域的“平均”比总损耗数据(Bm-W);然后按该平均值对整个铁心模型的总损耗进行均匀化处理,从而确定出模型在不同磁感应强度下的等效质量me。
蒋介石在国民党执政的二十余年间,随着个人权势及外在环境的变化,不同时期对于党义阐述的重点和指向会有不同,其宣导的对象亦在不断扩大,但随着国民党在大陆失败的临近,其宣导的效果及实际影响的范围不断衰微。
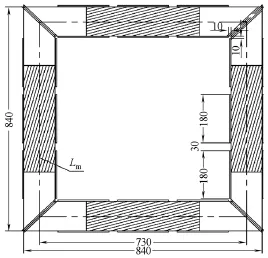
图2 等效磁路长度的确定示意图Fig.2 Determination of equivalent magnetic path length
在保证模型测量线圈的感应电压为正弦波形的前提下(电压畸变率控制在 THD<1.5%),得到两模型在相同磁感应强度下的有功功率,Model C1的测量值为P1,Model C2的测量值为P2。由于两模型除了“柱轭区”的长度不同外,其余的结构尺寸参数完全相同,因此,把两模型相应的功率测量数据相减,就得到大模型的柱-轭均匀化区域,即图2中阴影区域的有功功率∆P,即

根据模型阴影区域的尺寸和材料属性,可以得到模型阴影区域的质量∆m,再由式(4)就可以得到该区域的比损耗Ps。

基于 Model C1的总损耗 P1和比损耗 Ps计算Model C1的等效质量me1可由式(5)得出。

基于Model C2的总损耗P2和由式(4)得出比损耗Ps计算Model C2的等效质量me2,可由式(6)得出。

根据实验测得的损耗结果,利用式(2)、式(5)和式(6)就可以得出Model C1和Model C2在不同磁通密度下的等效磁路长度,分别如图3和图4所示。

图3 Model C1的等效磁路长度Fig.3 Equivalent magnetic path length of Model C1

图4 Model C2的等效磁路长度Fig.4 Equivalent magnetic path length of Model C2
从图3和图4可以看出,等效磁路长度随着叠片铁心内磁感应强度的变化而变化,总体来看等效磁路长度大于或等于几何平均磁路长度。由于等效磁路长度是根据铁心的有功损耗确定的,在铁心的“柱轭区”有功损耗分布近似为均匀的,因此,等效磁路长度的变化,实际上反映的是铁心“接缝区”有功损耗分布、的变化情况。由式(1)~式(5)可得
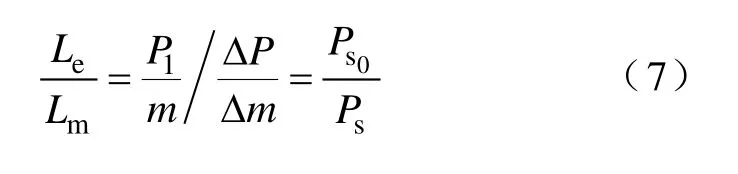
式中,Ps0是由整个模型得到的比损耗,Ps是由图2阴影区域得到的比损耗。由于铁心接缝区的平均损耗总体上要高于柱轭区的平均损耗[10],导致Ps0>Ps,表现为等效磁路大于几何平均磁路长度。在激励电流比较小时,铁心“接缝区”有功损耗分布对铁心总有功损耗分布的影响作用不明显,表现为等效磁路的变化比较平缓。随着激励电流的增加,接缝区有功损耗的增加速度要高于阴影区有功损耗的增加速度,表现为 Ps0的增加高于Ps的增加,导致等效磁路长度明显增长。当接缝区的磁通达到饱和时,其损耗几乎不再变化,此时Ps0达到最大值,等效磁路长度也达到最大值。随着激励电流的继续增加,由于阴影区磁通还没有进入饱和状态,Ps继续增加,导致等效磁路长度开始减小。当铁心阴影区磁通也进入饱和时,整个铁心都工作在饱和状态,此时 Ps0和 Ps接近相等[10],即等效磁路长度近似等于几何平均磁路长度。
由于等效磁路长度的变化,实际上反映的是铁心“接缝区”磁通和损耗分布的不均匀性,在这里“接缝区”不再简单地被看作是一条几何缝隙,在不同的磁感应强度下,铁心接缝可以扩展为一个以该“几何缝”为中界面的三维区域,如图 5所示,可称之为“接缝影响域(体积)”。实际上,这样处理扩展了“经典”方法的适用范围[11]。
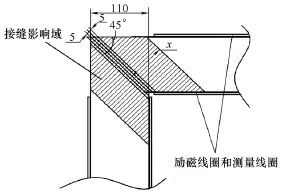
图5 接缝影响域示意图Fig.5 Core joint influence region(sketch)
图5中的x表示接缝影响域由铁心的几何接缝向铁心“柱轭区”延拓的距离,用以表征接缝影响域体积变化的情况。随着铁心饱和程度增加,接缝影响域将以接缝为界向两侧扩展。
4 叠片铁心的磁性能
采用双铁心模型法,通过实验测量结果可以确定出不同磁感应强度下模型的等效磁路长度,进而得到叠片铁心的磁化曲线(Bm-Hb)和损耗曲线(Bm-W),如图6和图7所示。需要指出,这里的Hb是磁感应强度达到最大值Bm时的磁场强度。为便于比较,图中给出了武汉钢铁公司提供的标准条件下测量得到的叠片材料磁性能数据曲线。

图6 叠片铁心的Bm-Hb曲线Fig.6 Bm-Hb curves of the laminated core
图6a表明,在低磁感应强度下,采用双铁心模型法得到的磁化曲线和在标准条件下测量得到的磁化曲线相比,两者差别不大。但在高磁感应强度下,两者的相差比较明显。图6b表现为,采用双铁心法得到的叠片材料的磁性能比标准条件下得到的材料磁性能要差一些,反映了叠片材料在实际工况下的真实属性。这表明在对硅钢叠片材料进行仿真计算时,需要对标准条件下得到的材料磁化曲线测量结果进行修正。

图7 叠片铁心的损耗曲线Fig.7 Bm-W curves of the laminated core
图7是采用双铁心模型法得到的损耗曲线和在标准条件下测量得到的损耗曲线,两者的差别反映了在不同磁感应强度下,铁心接缝区有功损耗对阴影区有功损耗的影响,符合材料的实际工况,因此得到的结果更合理。
图6b和图7b表明,工作条件下叠片铁心的磁性能有别于采用标准测量方法得到的磁性能,叠片铁心的实际磁性能曲线不能用标准条件下测量得到的磁性能曲线完全替代,这在对电力变压器叠片铁心以及磁屏蔽的磁通分布和损耗分布进行精细的数值计算和分析时应予以重视。
5 叠片铁心励磁伏安的分离
叠片铁心空载励磁伏安主要是由励磁电流的无功分量产生的,虽然当铁心达到饱和时,会产生一些漏磁通,但是在空载条件和一定的磁通密度范围内,作为一种近似的工程处理方法,可以认为总的励磁伏安只消耗在铁心接缝和接缝以外的“柱轭区”内。在对 “接缝区”和“柱轭区”进行励磁伏安分离时,需要确定接缝影响域的大小,也就是确定图5中的x值,计算公式如下:

式中,h为铁心的厚度,按照传统方法分离励磁伏安时,在本模型中x的取值为:(5+5)× 2≈14mm,即铁心搭接循环外延一个步长的位置。采用双铁心法进行励磁伏安分离时,x的取值为

式(8)实际上是对传统方法进行的扩展,在铁心等效磁路长度和几何平均磁路长度相等时,采用双铁心法和传统的励磁伏安分离方法得到的接缝影响域体积是相等的。假设铁心接缝影响域及接缝影响域之外的柱轭区域的励磁伏安分量分别设为qj和qc,则可以根据下式进行铁心励磁伏安的分离。
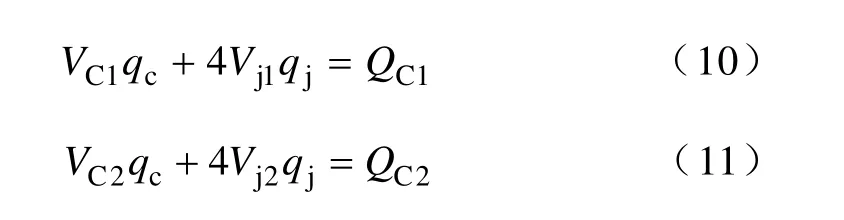
式中 VC1——Model C1接缝影响域之外铁心“柱轭区”的体积;
VC2——Model C2接缝影响域之外铁心“柱轭区”的体积;
Vj1——Model C1接缝影响域的体积;
Vj2——Model C2接缝影响域的体积;
QC1——测量得到的Model C1在某一磁通密度下的总无功励磁伏安;
QC2——测量得到的Model C2在相同磁通密度下的总无功励磁伏安。功率测量采用精密功率分析仪(WT3000,Yokogawa,Japan)。
根据式(7)和式(8),分别按照接缝影响域取固定值的“传统”方法(即 x=14mm)和本文提出的按照等效磁路方法确定的接缝影响域,进行励磁伏安分离得到的“柱轭区”和“接缝区”的励磁伏安曲线,如图8和图9所示。

图8 柱轭区励磁伏安曲线Fig.8 Bm-qc curves of the core leg-yoke region

图9 接缝区励磁伏安曲线Fig.9 Bm-qj curves of the core joint region
从图8可以看出,采用两种励磁伏安分离方法得到的叠片铁心“柱轭区”励磁伏安曲线的分布趋势相当吻合。而铁心“接缝区”的励磁伏安曲线,在较高磁感应强度时所得结果相差大一些,如图 9所示。由于传统的方法接缝影响域的大小为固定值,在进行励磁伏安分离时,不能反映铁心在不同磁感应强度下接缝影响域的变化,而等效磁路法采用等效磁路长度的变化来反映接缝影响域随磁通分布的变化情况,因此,励磁伏安分离所得结果更加符合叠片铁心的实际工作情况。
6 结论
电工材料的电磁特性精细模拟是提高工程电磁场问题的求解精度和数值仿真有效性的关键。本文针对现有材料性能数据不充分的情况,对叠积型全斜接缝铁心的综合电磁性能进行了模拟实验研究。
基于两个产品级的叠片铁心模型,采用“双铁心法” 确定了叠片铁心等效磁路长度,提出了接缝“影响域”的概念,考察了等效磁路长度和接缝影响域随磁通密度的变化情况,得到了叠片铁心在工作条件下的基本磁特性数据,并与传统的标准测量条件下得到的磁性能数据进行了对比。所得的结果对于实际变压器叠片铁心的电磁分析和铁心结构的优化设计具有一定的指导意义。但对铁心之外的漏磁通、铁心材料的各向异性等复杂情况的模拟需要进一步研究。
[1]Cheng Z, Hao R, Takahashi N, et al. Engineeringoriented benchmarking of problem 21 family and experimental verification[J]. IEEE Trans. on Magn.,2004, 40(2): 1394-1397.
[2]Cheng Z, Takahashi N, Yang S, et al. Loss spectrum and electromagnetic behavior of problem 21 family[J].IEEE Trans. on Magn., 2006, 42(4): 1467-1470.
[3]Cheng Z, Takahashi N, Yang S, et al. Eddy current and loss analysis of multi-steel configuration and validation[J]. IEEE Trans. on Magn., 2007, 43(4):1737-1740.
[4]Cheng Z, Takahashi N, Forghani B, et al. Analysis and measurements of iron loss and flux inside silicon steel laminations[J]. IEEE Trans. on Magn., 2009,45(3): 1222-1225.
[5]谢德馨, 杨仕友, 等. 工程电磁场数值分析与综合[M]. 北京: 机械工业出版社, 2009.
[6]程志光, 高橋則雄, 博札德·弗甘尼, 等. 电气工程电磁热场模拟和应用[M]. 北京: 科学出版社,2009.
[7]Marketos P, Zurek S, Moses A J. Calculation of the mean path length of the Epstein frame under non-sinusoidal excitations using the double Epstein method[J]. Journal of Magnetism and Magnetic Materials, 2008, 320(20): 2542-2545.
[8]Cheng Z, Hu Q, Jiao C, et al. Laminated core models for determining exciting power and saturation characteristics[C]. World Automation Congress Proceedings, 2008,Ⅰ-3: 1215-1218.
[9]用爱泼斯坦方圈测量电工钢片(带)磁性能的方法[S].北京: 中国标准出版社, 2008.
[10]辜承林, 周克定, 李朗如. 电力变压器铁心磁场和损耗分布的三维数值方法与实施(第三部分铁心搭选区)[J]. 中国电机工程学报, 1993, 13(5): 27-33.Gu Chenglin, Zhou Keding, Li Langru. Three dimensionol computation of flux and loss distributions in power transformer cores (part Ⅲ: overlapped joints)[J]. Proceedings of the CSEE, 1993, 13(5): 27-33.
[11]Hu Q. No-load current and magnetic field[R]. BTW Rsearch Rport, 2007.

