并行计算合成绝缘子串电压分布及金具表面电场强度

厉天威 阮江军 杜志叶 黄道春

（1. 广西电力工业勘察设计研究院 南宁 530023 2. 武汉大学电气工程学院 武汉 430072）

1 引言

合成绝缘子相对于玻璃和瓷绝缘子具有重量轻、强度高、耐污性能好、便于运输和安装、运行维护方便等优点，在国内外得到了广泛的应用[1]。但在运行过程中有出现芯棒脆断的情况，分析表明主要是高压端部电场强度较高，电晕严重，产生电腐蚀并加剧酸腐作用的结果[2]，所以必须降低高压端的电压分布。随着电网超高压的发展，在线路上发生污闪事故的绝缘子几乎都损坏了均压环、端部金具及金具附近的伞裙、护套。这些被损坏的绝缘子有很多是由于绝缘子端部区域的场强过高引起的，给电网的安全运行带来极大的危害。计算合成绝缘子串的电位分布以及金具表面的电场强度并以此来采取防护措施势在必行。文献[1]和文献[3]用三维有限元法计算高压输电线路的绝缘子串的电位分布，由于单机计算速度和内存大小的限制，网格剖分数量有限，因此计算结果会存在一定的误差。本文通过并行计算进行分析及对比，来得到复合绝缘子串电位分布和金具表电场强度，以确定绝缘子串屏蔽环的最优位置并降低绝缘子串端部电场强度。

有限元并行计算已经成为解决大规模数值计算问题的最重要手段之一[4-6]。有限元并行最直接和最初的实现是利用数值并行求解器对传统有限元最耗时的线性方程组求解过程进行并行化求解以加快整个分析过程[7-11]，即线性方程组的求解是并行过程，而单元分析和线性方程组的形成是串行过程。为进一步提高并行效率，本文提出采用区域分解法[12-15]“分而治之”的并行策略在分布式存储的并行环境下实现有限元并行计算，即将有限元求解区域划分成若干大小近似相等的分区，然后将这些分区信息映射到各个处理器上并行地进行计算。每个处理器负责该分区的全部计算，通过消息传递方式与其他处理器交换分区边界数据信息。该并行策略在单元级上实施有限元并行求解，避免形成总体刚度矩阵，其优点在于计算高度并行化和数据通信量少。

本文建立了500kV高压输电线路合成绝缘子串的三维有限元模型，运用基于非重叠型区域分解的并行计算技术对绝缘子串的电位分布以及金具表面的电场强度进行计算来优化屏蔽环位置，确定并降低绝缘子端部电场强度。

2 非重叠型区域分解法

根据分区是否重叠，区域分解法分为重叠型区域分解法和非重叠型区域分解法。两种分区方法如图1所示。

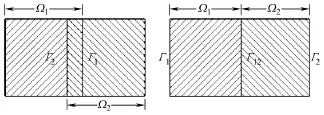
图1 重叠型和非重叠型区域分解Fig.1 The overlapping and non-overlapping domain decomposition

以Schwarz交替法[12]为基础的重叠型区域分解算法的基本思想是把求解区域Ω 分解为两个或多个较小的相互重叠的分区Ω1，Ω2，…，Ωn，然后在这两个或多个分区之间交替求解，最终得到整个求解区域的解。Schwarz交替法的边值问题为

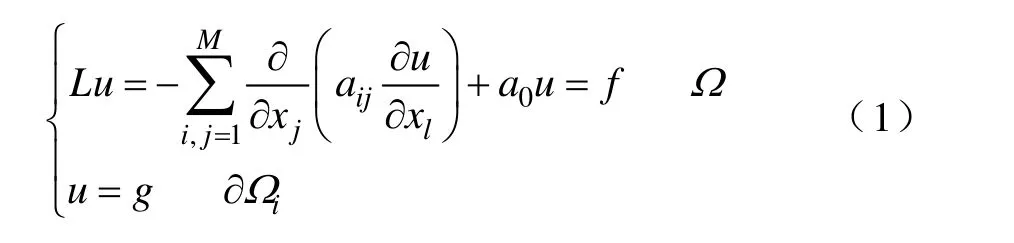
其中，aij为对称正定矩阵，a0≥0。把求解区域Ω 分解为 M个分区，当Ωk与Ωm相邻时，Ωk∩ Ωm≠ ∅ 。选择初始近似 u0∈(Ω )，n=0，则并行计算各分区上边值问题为

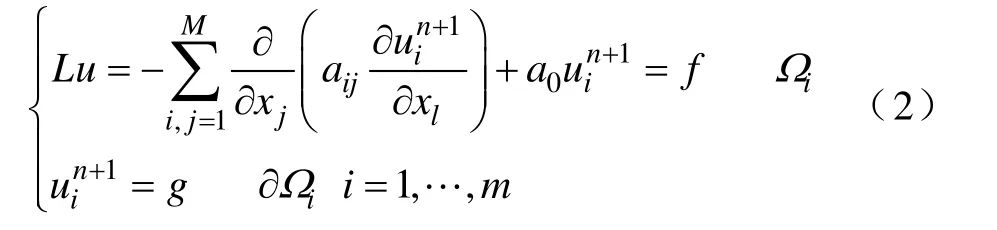
再令n=n+1继续迭代，直至收敛。

基于Schwarz交替法的重叠型区域分解法，各分区与其他分区有重叠，重叠区域中的未知量与多个分区相关联，因而计算量相对较大。其计算效率取决于重叠区域的大小，当分区个数增多时迭代收敛速度减慢，特别对于三维问题，增加重叠区域严重制约了计算速度的提高。

对于椭圆形偏微分方程的边值问题，非重叠型区域分解算法的边值问题为

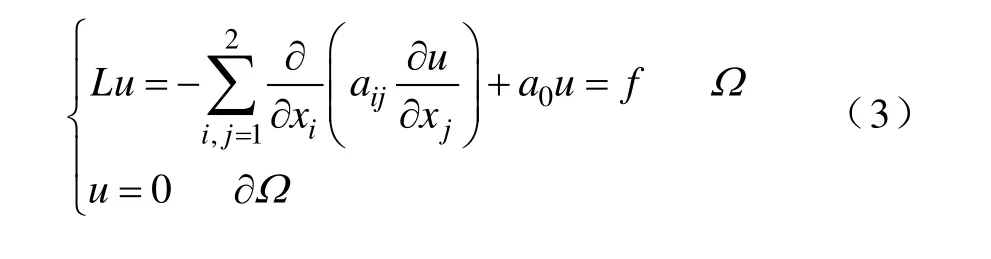
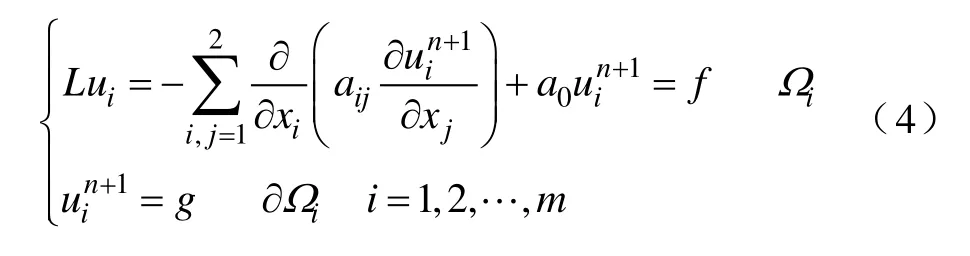
如何在减少重叠区域的同时不降低迭代收敛速度成为本文所关注的问题。对于非重叠型区域分解，只有区域之间的边界上的变量与多个分区相关联，迭代计算速度更快。因此，本文采用非重叠型区域分解法来进行并行求解。

3 并行计算实现

3.1 网格划分

对于有限元网格如图2a所示，利用METIS（分区软件）对该网格划分了3个分区。分区结果如图2b所示。其中各分区的单元的尖点（部分节点）都在与之相邻的分区上，在实行有限元并行求解时需要利用消息传递的方式来更新这些节点的值。在图2c中，处理器Proc 0在进行计算时，除了包括该分区里的所有节点和单元外，还必须包括与这些节点相关联的外边界单元的信息，如虚线所示的单元。因此，在图2b的单元分区结果的基础上，进行的分区后处理的结果如图2d所示。对于图2d中的三个分区，各处理器需要计算的节点在图中的分界线以内，各分区相关联的相邻分区中的节点在分界线以外并靠近分界线，各分区的单元为标有同样标记的节点构成的所有单元之和，如图打点标记。

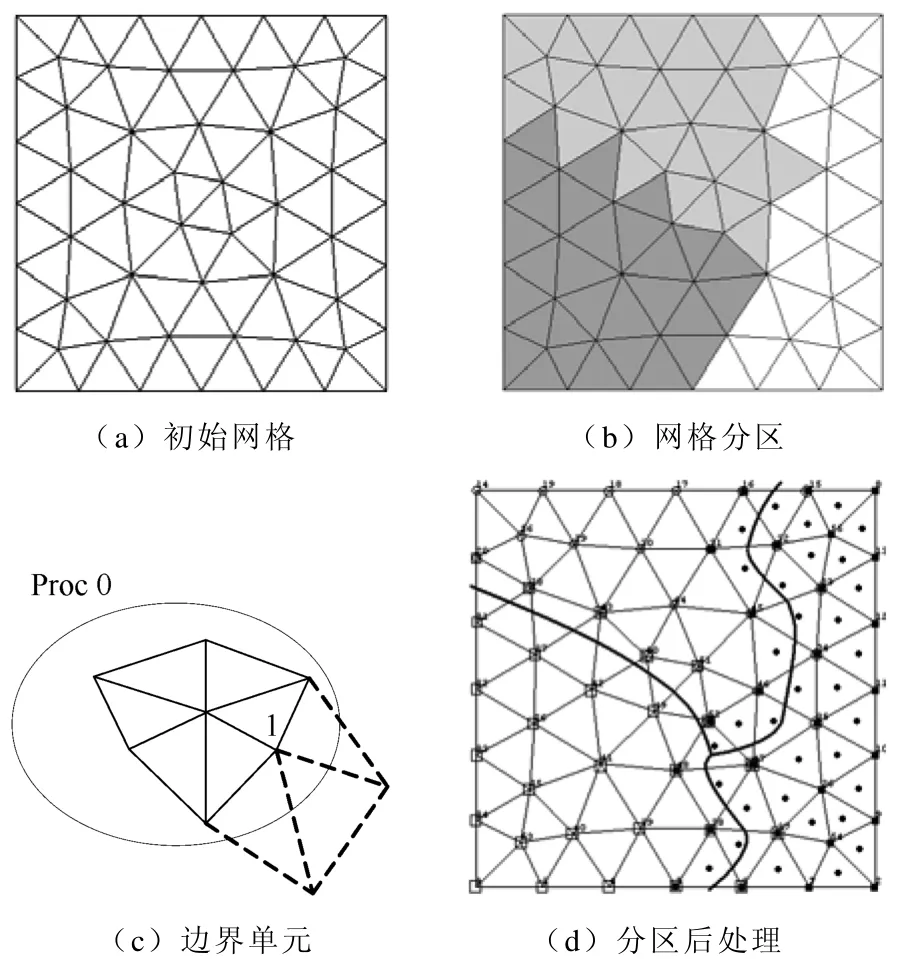
图2 非结构化网格分区示意图Fig.2 The sketch map of unstructured mesh partition

3.2 刚度矩阵的形成

有限元分区的邻接图如图3所示，整个求解区域被划分成3个分区，分别分配给3个处理器Proc 0、Proc 1和Proc 2进行并行计算。

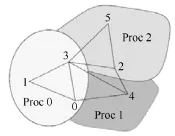
图3 邻接图Fig.3 The adjacency graph

若用单处理器对整个求解区域进行求解，需要形成总体刚度矩阵。而在各分区内单独形成刚度矩阵时，各分区刚度矩阵分别对应于总体刚度矩阵的多行，如图4所示。如Proc 0、Proc 1和Proc 2分别对应总体刚度矩阵的{0,1,3}行、{4}行和{2,5}行。

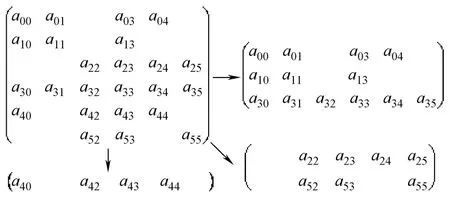
图4 分布式系数矩阵的形成Fig.4 The formation of distributed coefficient matrices

3.3 数据通信

MPI[16]（消息传递函数库）提供了与C、Fortran和C++语言的绑定，适用于分布内存的并行计算机系统。MPI程序采用的是SPMD（单程序多数据流）执行模式，即一个程序同时形成多个独立的进程，各进程由独立操作系统调度，享有独立的CPU和内存资源。进程间通过消息传递互相交换信息，消息传递快可以减少各处理器间的等待时间，从而提高并行度和并行计算效率。

为了充分利用主节点的高计算性能，并且考虑到利用相同的数值计算方法在单机上计算结果有助于对比分析并行计算的效率，本文采用对等模式来替代主从模式，对等模式基本框架如图5所示。对等模式即程序中各进程（包括控制部分）地位相同，只是处理的数据不同，且程序可以利用单个进程运行。由图可知，进程0除了发送和接受数据外还承担着计算的任务。

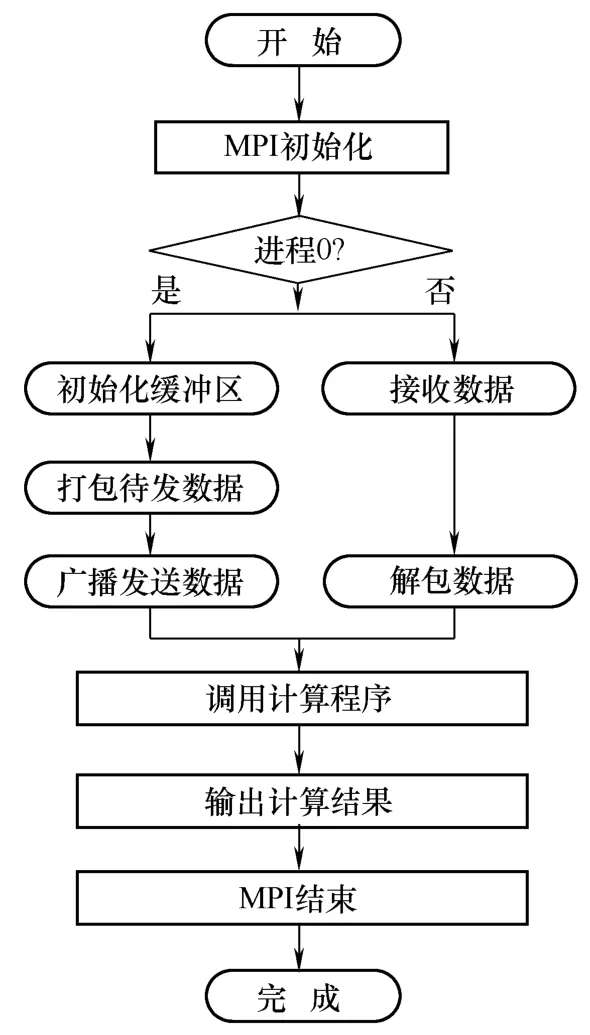
图5 对等模式并行程序基本框架Fig.5 The basic frame of equal mode parallel program

各处理器间的数据交换主要表现为：在前处理阶段，主处理器把各分区的单元节点信息发送到各从处理器，数据量较大，只需要传递一次；在迭代开始后，各主、从处理器把新的边界节点值传递到相邻处理器来更新边界节点值，数据量相对较小。这些处理器之间的数据交换通过调用MPI库函数来实现，采用非阻塞通信的方式来减少数据交换时间，以提高数据传输效率。网格分区后的各个分区的单元和节点数据均存储在各处理器所在存储器中，实现存储局部化，这样每个分区可以很方便存取需要的数据。各分区的刚度矩阵、荷载向量、分区的边界节点值和中间计算结果都存储在处理器所在存储器中，这样大大降低各处理器之间通信。

本文采用并行预处理共轭梯度法等对各分区线性方程组进行迭代求解，每一步迭代都要与相邻的分区交换更新数据，调用 MPI函数库中提供的MPI_Send，MPI_Recv等函数可以方便地实现数据交换。

4 算例及分析

4.1 控制方程

输电线路通电情况下其周围工频电场变化频率很低，属准静态场范畴。当电场的变化频率很低时，库仑电场远大于感应电场，即0Bt∂∂≈，于是有

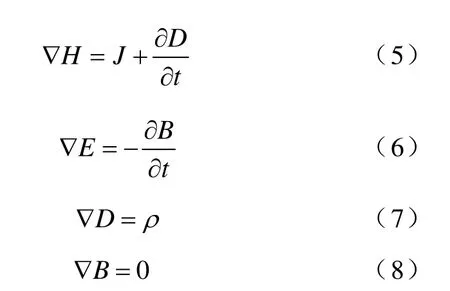
若只考虑电场，则用电流连续性方程代入式（5），且不考虑式（7），则准静态电场的控制方程可表示为

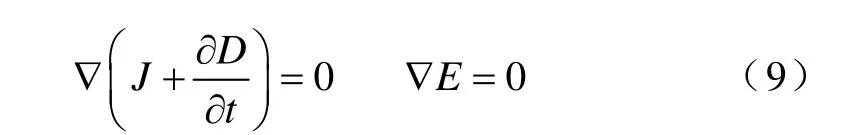
而J=σE，D= ε E，且有E =-∇φ ，故

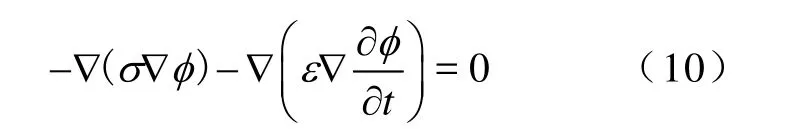
其复数形式为

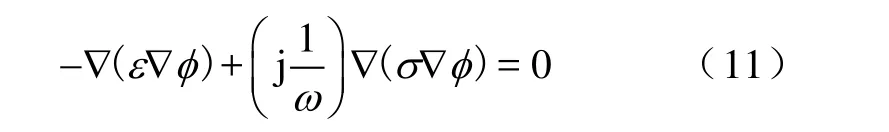
假设电介质都为均匀介质，于是本文计算静态电磁场的泊松方程可表示为

4.2 并行计算合成绝缘子串电位分布

为了给合成绝缘子的设计运行提供参考，本文运用有限元并行计算方法来计算 500kV高压输电线路合成绝缘子串上的电压分布。绝缘子型号为FXBW2—500/160，大伞43片，小伞42片，结构高度为 4450mm，绝缘子介电常数为 3.5，两端金具长度分别为150mm，屏蔽环外径280mm；采用4分裂导线LGJ—400/50，分裂间距为450mm，导线长 20m；横担宽、高各 0.8m，长 16m。考虑到实际线路结构的对称性和计算机的计算能力有限，以导线侧芯棒端部中心为坐标原点，只对绝缘子串、金具、导线和横担的1/4部分建立三维模型进行分析，最后用空气包围起来，模拟无穷大区域。图6a为合成绝缘子串的三维模型，图6b为该模型外包空气层后的1/4模型。为验证本文算法正确性，对图6b的三维模型采用4节点的四面体单元分别剖分为27 868和115 291个节点，基于区域分解法的思想，对该单元网格进行分区，来进行并行求解。

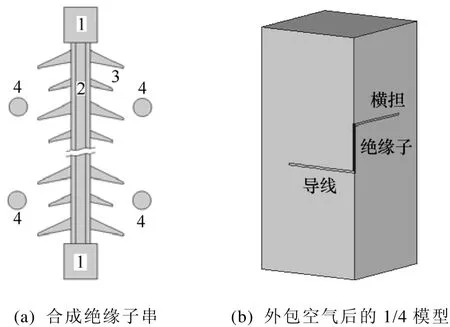
图6 合成绝缘子串三维分析模型Fig.6 The 3D model of composite insulator string under the transmission line and the rung

在本研究室的机群环境下（6节点，Fedora core 2.0操作系统），并行计算程序采用MPI消息传递的并行编程的对等模式，数值求解方法用C++语言编写实现，本文在芯棒中间位置均匀选取40个有代表性的点，精确计算得到各点的值作为参考。图7为各绝缘子的耐受电压百分比，横坐标1～40是绝缘子串上依次从高压端到低压端上点的编号，可以看出并行计算和单机计算的结果能够很好地吻合，从而验证了本文运用以上并行求解算法计算的正确性。

图7 并行计算与单机计算结果比较Fig.7 Comparison between sequential and parallel computation

运用各种线性方程组并行求解器PCG（预处理共轭梯度法）和 GMRES（广义最小余量法）等分别对各分区内形成的线性方程组进行并行求解，求解器的计算时间与处理器数目之间的对比如图8所示。可以看出，随着处理器数目增加，各求解器计算时间在不断减少。在求解精度相同的情况下，BICGSTAB（稳定双共轭梯度法）法计算时间最少，CGS（复共轭梯度平方法）法和 GMRES法次之，CG（共轭梯度法）法计算时间最长。

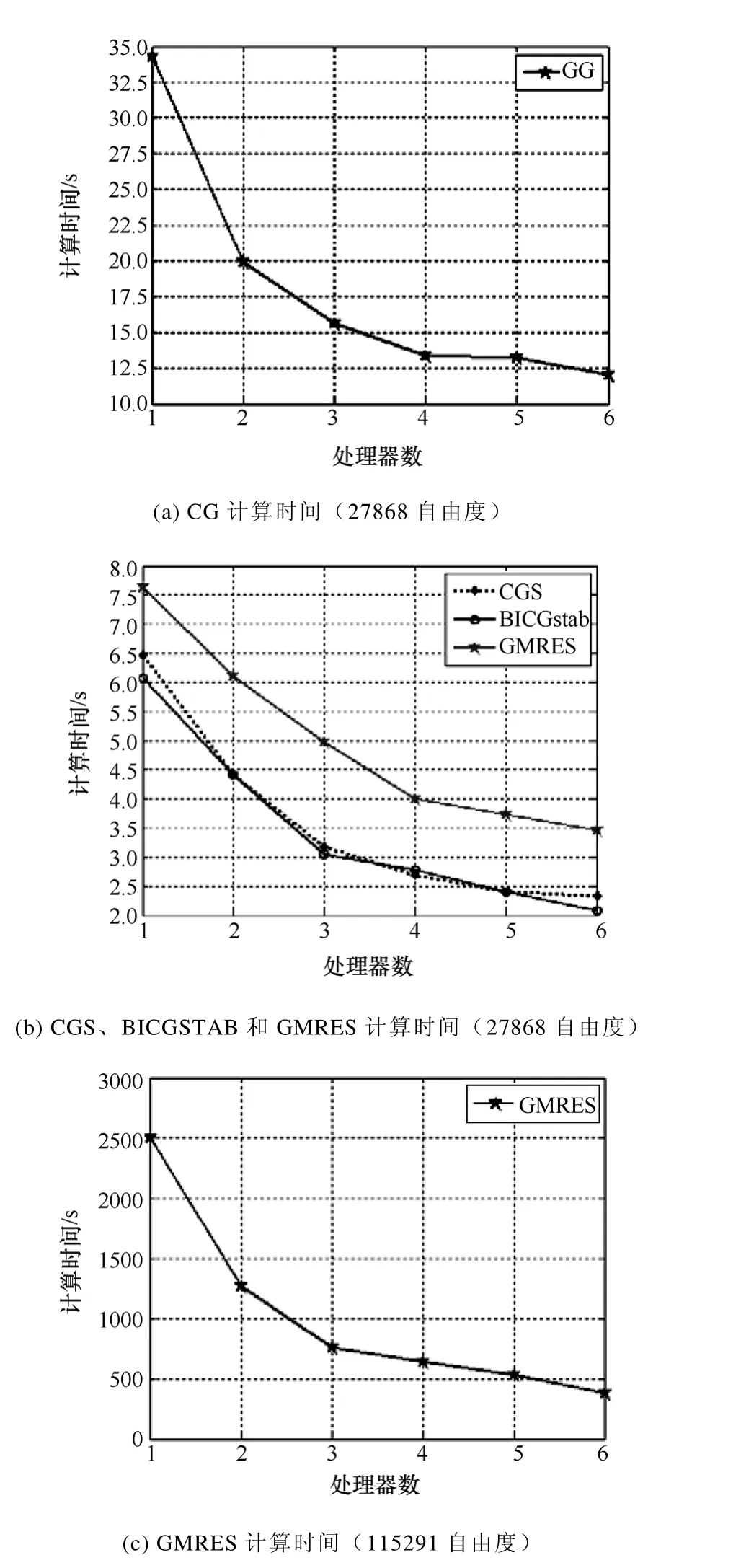
图8 各求解器计算时间与处理器数目的对比Fig.8 Time comparison for the number of processors

并行计算加速比和效率是衡量并行计算机系统和并行算法优劣的两个基本指标。图9a为利用GMRES计算得到的并行计算加速比和效率。可以看出，当计算量较小时，六处理器加速比为2.2。因为数据量较少，数据交换时间在整个计算过程中占的比重较大，导致加速比不高。计算量增大时，随着处理器数目的增多，计算时间不断地减少，出现了超线性加速情况，即 s(n)＞n（s(n)为加速比，n为处理器数）。超线性加速是由于在机群中每个处理器可以访问的内存容量与单处理器拥有的内存容量相同，因此，在任何时刻总能保存更多的数据，减少了对工作速度相对较慢的硬盘的访问。从图9b可以看出，并行计算效率随着处理器的增加有减小的趋势。根据以上分析，适当增大处理器数目可以减少计算时间，并保证较高的求解效率。因算法特点不同，各求解器迭代次数也不同，迭代次数越多，处理器间数据交换越频繁，对于27 868自由度规模的问题，各求解器迭代次数见下表。

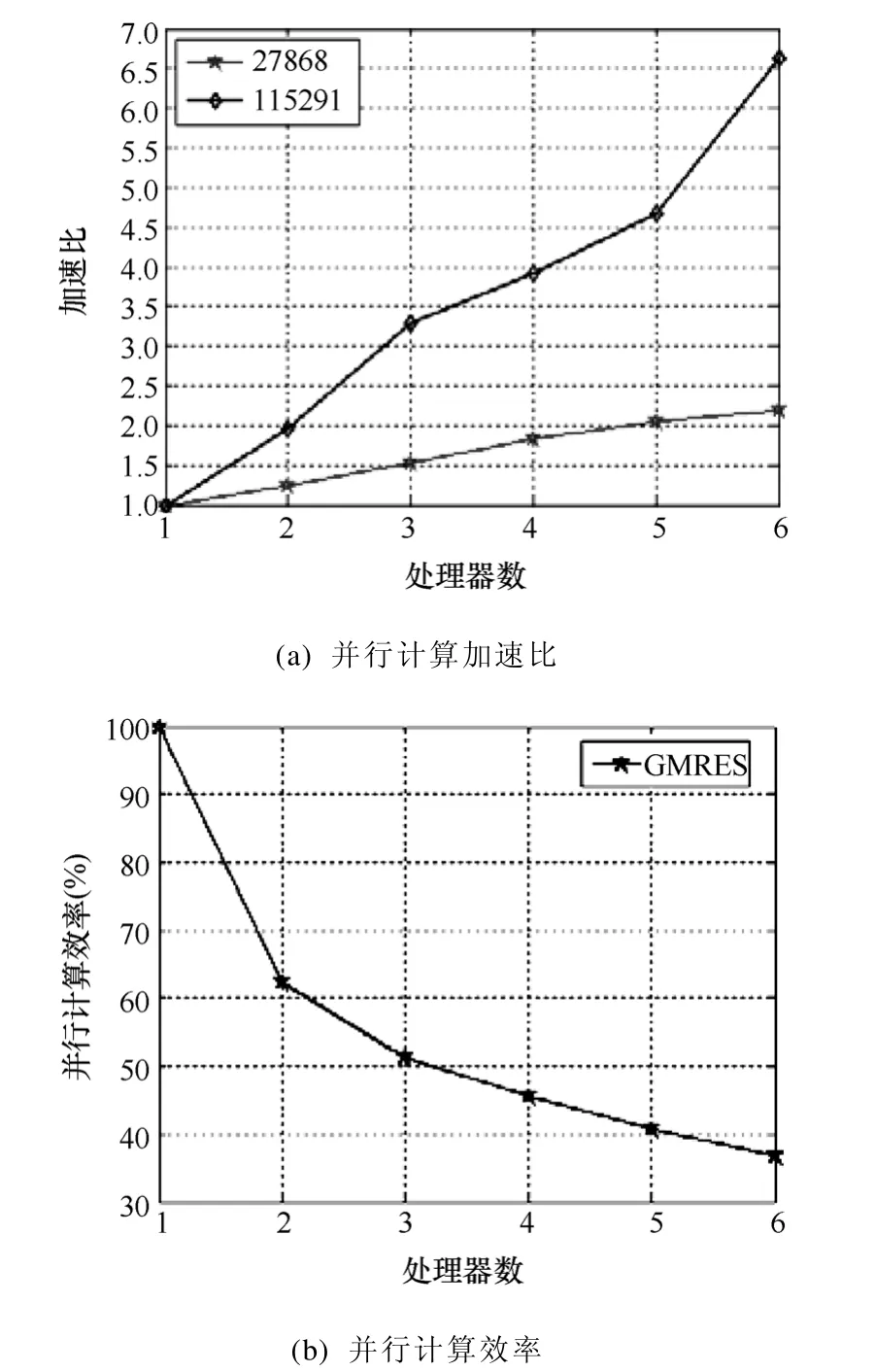
图9 并行计算加速比和求解效率Fig.9 The efficiency of parallel computation

表 各求解器迭代次数比较Tab. The iterative numbers of the solvers

4.3 并行计算金具表面电场强度

基于4.2节并行算法正确性的验证，现以500kV高压输电线路复合绝缘子为例，考虑杆塔、导线和屏蔽环等因数的影响，对金具表面的电场强度进行并行计算。根据对称性建立有杆塔的四分之一模型，采用4分裂导线，如图10a所示，网格剖分如图10b～图10c所示，高压端电位分布如图10d所示。本文首先对整体网格模型进行分区，分区数目为2～6个，然后分别利用 2～6个处理器来进行计算。其中，6个分区的分区结果如图11所示，分区过程综合考虑了负载平衡等因素，各分区计算量大致相等。

首先对绝缘子周围电场分布进行计算，研究对象的取值点如图12右，在每片绝缘子的大小两个伞裙之间、小伞的下方处取点，共42个。由图12左可知单机和并行求解的结果能够很好地吻合，在上、下屏蔽环附近，电场强度有急剧增大的趋势，可知绝缘子周围电场强度的最大值在下屏蔽环附近，大约为920kV/m，未达到均匀电场中击穿场强的峰值(3000kV/m)。随后，本文依次对绝缘子上、下铁帽和导线周围线夹表面电场强度分别进行了计算，计算结果和取值点分别如图13所示，为进一步分析电晕特性等提供了依据。在上铁帽和下铁帽周围0.09m处取21个点。在离线夹所在平面0.02m处分裂导线周围取21个点，这些点均匀分布在以分裂导线中心为圆心，半径为1.2R的半圆上，R为四分裂导线分裂半径。

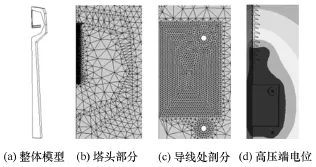
图10 500kV输电线路模型及网格图Fig.10 The model of 500kV transmission lines and the mesh

图11 六个分区网格图Fig.11 The six partitions mesh graph

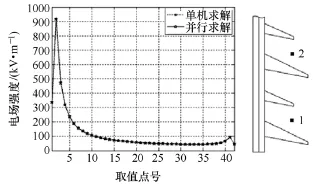
图12 绝缘子串周围电场分布Fig.12 The electric field around the insulator

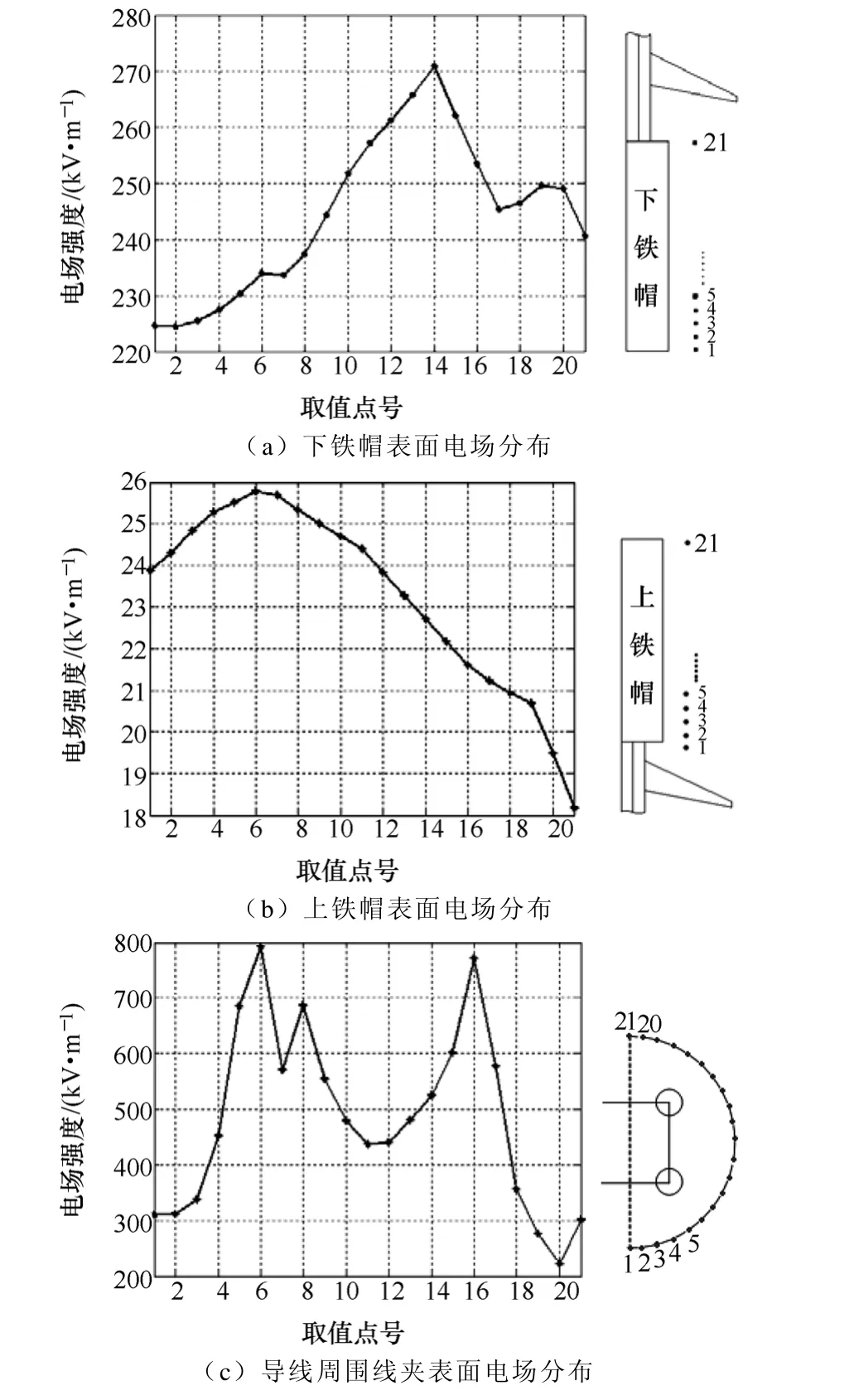
图13 金具表面电场分布Fig.13 The electric field intensity distribution on the surface of hardware fittings

5 结论

本文利用多台 PC机构建的并行计算机系统，基于非重叠型区域分解法，采用消息传递的并行编程对等模式，对三维有限元计算的数学模型开发了SPMD的并行程序，实现了对500kV高压输电线路的绝缘子串电位分布和金具表面电场强度的并行计算。计算结果表明并行计算系统相对于单机计算可以加快计算速度，获得良好的加速比。以合成绝缘子串电位分布的结果为依据来优化屏蔽环位置，通过计算复合绝缘子串金具表面电场强度，以确定并降低绝缘子端部电场强度。

[1]司马文霞, 杨庆, 孙才新, 等. 基于有限元和神经网络方法对超高压合成绝缘子均压环结构优化的研究[J]. 中国电机工程学报, 2005, 25(17): 115-120.Sima Wenxia, Yang Qing, Sun Caixin, et al.Optimization of corona ring design for EHV composite insulator using finite element and neural network method[J]. Proceedings of the CSEE, 2005,25(17): 115-120.

[2]张鸣, 陈勉. 500kV罗北甲线合成绝缘子芯棒脆断原因分析[J]. 电网技术, 2003, 27(12): 51-53.Zhang Ming, Chen Mian. Anlysis on core brittle fracture of composite insulators in a certain 500kV transmission line[J]. Power System Technology, 2003,27(12): 51-53.

[3]沈鼎申, 张孝军, 万启发, 等. 750kV线路绝缘子串电压分布的有限元计算[J]. 电网技术, 2003, 27(12):54-57.Shen Dingshen, Zhang Xiaojun, Wan Qifa, et al.Calculation of voltage distribution along insulator strings of 750kV by finite element method[J]. Power System Technology, 2003, 27(12): 54-57.

[4]谢德馨, 唐任远, 王尔智, 等. 计算电磁学的现状与发展趋势——第14届COMPUMAG会议综述[J].电工技术学报, 2003, 18(5): 1-4.Xie Dexin, Tang Renyuan, Wang Erzhi, et al. Major achievements and future trends of computational electromagnetics—summary of the 14th conference of compumag[J]. Transactions of China Electrotechnical Society, 2003, 18(5): 1-4.

[5]钟建英, 林莘, 何荣涛. 自能式 SF6断路器熄弧性能的并行计算仿真[J]. 中国电机工程学报, 2006,26(20): 154-159.Zhong Jianying, Lin Xin, He Rongtao. The parallel computation simulation of the extinguishing arc performance in the self-extinguished SF6circuit breaker[J]. Proceedings of the CSEE, 2006, 26(20):154-159.

[6]Butrylo B, Musy F, Nicolas L, et al. A survey of parallel solvers for the finite element method in computational electromagnetics[J]. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2004, 23(2):531-546.

[7]刘洋, 周家启, 谢开贵, 等. 基于 Beowulf 集群的大规模电力系统方程并行 PCG 求解[J]. 电工技术学报, 2006, 21(3): 105-111.Liu Yang, Zhou Jiaqi, Xie Kaigui, et al. Parallel PCG solution of large scale power system equations based on Beowulf cluster[J]. Transactions of China Electrotechnical Society, 2006, 21(3): 105-111.

[8]Watanabe K, Igarashi H. A parallel PCG method with overlapping domain decomposition[C]. 12th Biennial IEEE Conference on Electromagnetic Field Computation,2006: 49.

[9]Ito F, Amemiya N. Application of parallelized SOR method to electromagnetic field analysis of superconductors[J]. IEEE Transactions on Applied Superconductivity, 2004, 14(2): 1874-1877.

[10]Vollaire C, Nicolas L. Preconditioning techniques for the conjugate gradient solver on a parallel distributed memory computer[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3347-3350.

[11]吉兴全, 王成山. 电力系统并行计算方法比较研究[J]. 电网技术, 2003, 27(4):22-26.Ji Xingquan, Wang Chengshan. A comparative study on parallel processing applied in power system[J].Power System Technology, 2003, 27(4): 22-26.

[12]吕涛, 石济民, 林振宝, 等. 区域分解算法—偏微分方程数值解新技术[M]. 北京: 科学出版社,1999.

[13]Imre Sebestyén. Electric-field calculation for HV insulators using domain-decomposition method[J].IEEE Transactions on Magnetics, 2002, 38(2): 1213-1216.

[14]Liu Peng, Jin Yaqiu. The finite-element method with domain decomposition for electromagnetic bistatic scattering from the comprehensive model of a ship on and a target above a large-scale rough sea surface[J].IEEE Transaction on Geoscience and Remote Sensing,2004, 42(5): 950-956.

[15]Liu Y Q, Yuan J S. A finite element domain decomposition combined with algebraic multigrid method for large-scale electromagnetic field computation[J]. IEEE Transactions on Magnetics, 2006,42(4): 655-658.

[16]都志辉. 高性能计算并行编程技术: MPI并行程序设计[M]. 北京:清华大学出版社, 2001.