基于自适应观测器的异步电机无速度传感器模糊矢量控制

张永昌 赵争鸣

（清华大学电机系电力系统国家重点实验室 北京 100084）

1 引言

无速度传感器技术由于其一系列优点如降低码盘安装的复杂性和成本，提高可靠性和减少维护等，自提出以来得到了广泛的研究和应用[1-9]。目前主要的无速度传感器方法包括开环计算、模型参考自适应和基于观测器的方法等。其中基于观测器的方法由于引入了误差闭环，提高了系统的鲁棒性和动态性能[2]，而且在观测磁链的同时可以对电机转速和部分电机参数进行辨识，是无速度传感器技术的一个热点。

状态观测器在应用中的一个主要问题是反馈增益矩阵的选择。传统的方法[6-7]将观测器的极点设计为正比于电机的极点，且出于收敛速度考虑，通常选择比例系数大于 1。这种方法的缺点是在放大观测器极点的实部同时放大了虚部，而后者有可能在高速时造成系统的不稳定。文献[8]提出将观测器的极点相对于电机极点在复平面上左移一个常数距离，由于只改变了极点的实部，系统的稳定性得到了提高。文献[8]中的观测器建立在以电机转速旋转的坐标系上，选择定子磁链和转子磁链为状态变量，得到的增益矩阵表达式比较繁复，不利于实际实现，其实验中采用高性能的浮点DSP，提高了系统的成本。另外，现有文献[6-9]给出的增益矩阵中通常含有估计转速，因此不可避免地受到转速估计误差的影响。借鉴文献[8]的方法，本文推导得出了在静止坐标系上的增益矩阵，并进行了简化，使其表达式中只含有常数，降低了转速估计误差对观测器的影响，其有效性通过实验结果得到证实。最后，本文还引入了负载转矩观测器以加快速度估计的动态响应[8]。

高性能的电机控制通常需要转速和磁链的闭环。矢量控制实现了转速和磁链的解耦控制，但它严重依赖于系统参数，而实际系统参数又很难准确获得，且随着系统运行状况也会发生变化，采用PI控制难以在整个运行范围获得良好的控制效果。模糊控制是基于模糊逻辑或模糊推理系统的控制算法，它是以人的经验和知识为基础，不需要精确的数学模型，对参数变化的线性或非线性对象有很强的鲁棒性。目前已有文献[10-12]将模糊控制用于间接矢量控制系统中，取得了良好的效果。本文采用直接矢量控制，在转速外环和磁链外环中采用模糊控制，并与采用PI控制时的效果进行了对比，证明了模糊控制的有效性。

在实际三电平中点钳位逆变器平台上搭建了直接矢量控制系统，对本文提出的方法进行了实验验证。实验结果表明，采用模糊控制和自适应观测的无速度传感器系统在全速域范围内具有良好的动静态性能，对参数变化和负载扰动具有较好的鲁棒性。

2 模糊转速和磁链控制

典型的模糊控制包括三部分，首先是输入变量模糊化，然后是模糊推理，最后是解模糊得到输出。图1给出了本文采用的二维模糊控制的框图，输入为误差e和误差变化率de/dt，输出为控制增量du，积分后得到实际控制量 u。输入和输出变量定标后的论域范围为[-1.4, 1.4]。本文的输入输出定标因子分别为Ke=1.0，Kce=120，Ku=600。输入变量模糊化语言值选为 7个：正大（PB）、正中（PM）、正小（PS）、零（Z）、负小（NS）、负中（NM）和负大（NB）。输出由于在原点（稳态点）附近要求信号更加精确，采用9个模糊语言值描述。与输入相比，增加了正正大（PVB）和负负大（NVB）。为简化计算，隶属度函数按三角形分布，且取为非对称的不规则三角形，当控制器输入变化量大时输出变化量也大，而在误差较小时输出也小，即在零附近调节更加精细，有利于系统稳定和提高静态性能。图2a和图2b是输入隶属函数分布，图2c是输出隶属函数分布，图2d是模糊控制器的输出曲面。

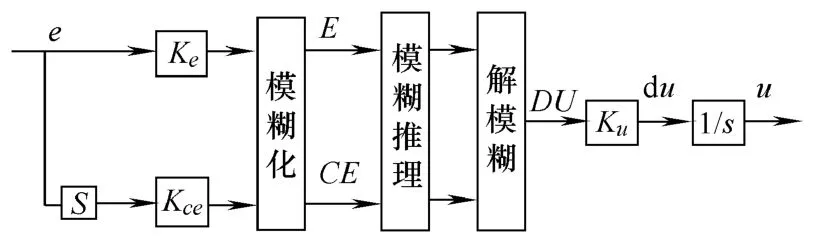
图1 模糊控制框图Fig.1 Block diagram of FLC

图2 模糊控制器隶属度函数和输出曲面Fig.2 Membership functions and output surface of FLC

模糊规则库是模糊推理的核心，本文采用的模糊控制规则见表1。采用Mamdani型模糊推理算法，模糊推理合成规则为“极大-极小”合成规则，最后的解模糊采用重心法得到输出。将上述模糊控制器用到转速和磁链控制中，转速FLC的输入为给定转速和估计转速的误差，输出为转矩电流。磁链FLC的输入为给定磁链和估计磁链的误差，输出为励磁电流。为简单起见，二者采用同一个FLC，仅输入定标系数和输出定标系数不同。在DSP实现时，为了减小计算量，采用二维插值查表的方法实现。即先离线计算把图 2d所示的模糊控制曲面以表格的形式存到DSP中，在实时计算时再查表输出。为了不显著增加存储量同时又不丧失输出精度，采用了二维线性插值的方法来计算输出。

表1 模糊控制规则表Tab.1 Rule matrix of FLC

3 转速自适应磁链观测器

3.1 观测器数学模型

以定子电流矢量和转子磁链矢量为状态变量，异步电机在两相静止αβ坐标下的数学模型可以用空间矢量[13]表示为

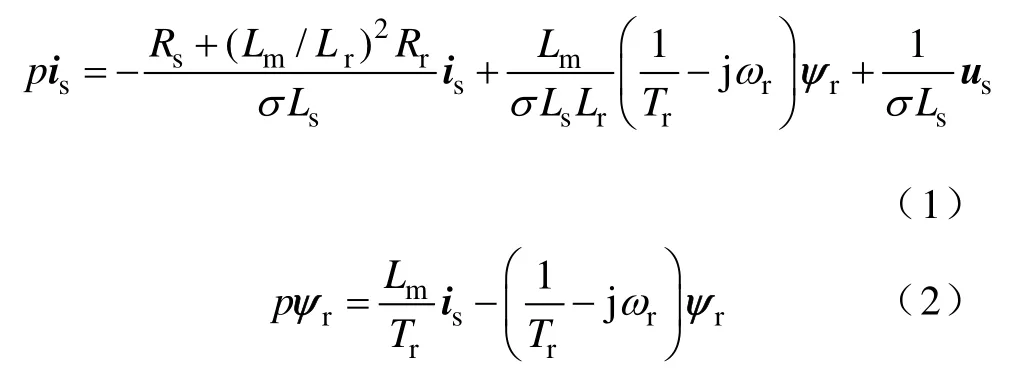
式中 Rs, Rr——电机定子电阻、转子电阻；

Ls, Lr, Lm——电机定子电感、转子电感、定转子互感；

ωr——电机转速；

Tr——转子时间常数，rrr/T L R= ；

us, is——αβ坐标下的定子电压矢量、定子电流矢量；

ψr——转子磁链矢量；p——微分算子。

基于式（1）和式（2）可得相应的异步电机观测器模型为

式中，“^”表示对应变量的估计值；G1=-( g1r+ jg1i)，G2=- ( g2r+ jg2i)均为增益系数。

3.2 观测器增益选择

增益选择是观测器应用中的一个难点，它直接影响着观测器的收敛速度和稳定性。经典方法中令观测器极点POb正比于电机极点PIM，即POb=kPIM，k为比例系数且一般大于1。这种方法由于在放大极点实部的同时也放大了虚部，因此可能在高速时造成不稳定。满足 POb=kPIM条件的增益矩阵不止一组[9]，其中一组比较简单的解为

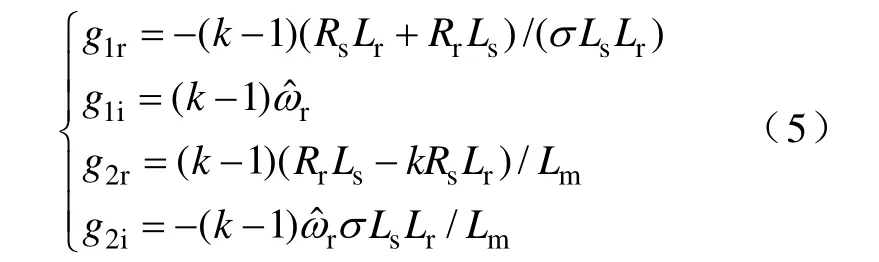
保持观测器极点的虚部不变，而将实部在复平面上向左平移，即POb=PIM+b（b＜0），在静止坐标系下推导得出增益的表达式为

在无速度传感器应用中，G2增益中含有的转速ωr要换成估计的转子转速rˆω，因此会受到估计转速精度的影响，而且由于是时变的，在计算中要实时更新，增加了实现的难度。为了简化计算，本文提出一种简化算法，即令rω→∞，相应的增益矩阵变为常数，简化计算，有利于实时实现，如式（7）所示。

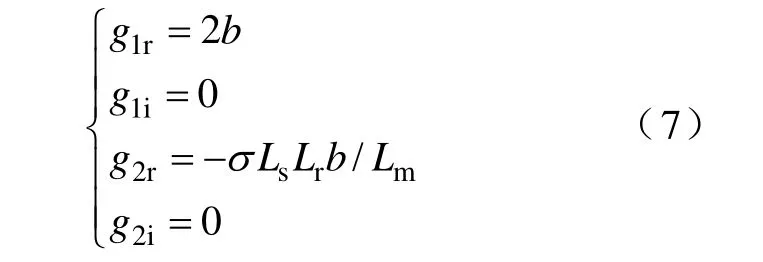
图3给出了 POb=kPIM和 POb=PIM+b(ωr→∞)两种情况下的电机和观测器极点的对比。其中 k=1.4，b=-40。图3a中的观测器极点在转速较高时有较大的虚部，可能导致观测器不稳定，且增益中包含转速；图3b中观测器极点相对电机极点向左移动，高速时虚部较小，系统稳定性提高，而且计算简单，容易实现。

图3 不同增益矩阵下的电机和观测器极点Fig.3 Motor and observer poles at different gain matrixes

3.3 速度辨识和转矩观测

利用 Lyapunov定律可以推导得出转子转速和定子电阻的自适应律，类似证明过程可见相关文献[6-9]。这里不再重复证明，而直接给出结果如式（8）和式（9）所示。

式中， ∆ is= is-为测量电流和观测电流之差；k1和k2为正常数。实际中为了提高动态响应速度，采用PI来代替式（8）和式（9）中的纯积分。

引入转矩观测的速度辨识可以用式（10）和式（11）来表示。

Kω、KT——正常数。

式（10）和式（8）相比，引入了电机运动方程，可以加快转速估计的动态响应。

4 仿真和实验结果

为了验证本文算法的有效性，采用Simulink进行了仿真。三电平逆变器存在中点平衡的问题，本文采用滞环控制的方法，根据中点电位偏差和负载电流方向来调节正负小矢量的作用时间比例[14-15]，从而保持中点平衡。系统框图如图4所示，仿真和实验参数见表 2。在仿真时为减少仿真时间，转动惯量取为J=0.01kg·m2，其他与实验均一致。从图5所示的电机起动和高速 1500r/min正反转波形可以看出，采用本文的新型观测器后（见图 5b），估计转速更加平滑，更接近实际转速，稳态误差也更小，相比传统的全阶观测器性能更好。

图4 三电平变频调速无速度传感器矢量控制系统Fig.4 Sensorless vector control system for three-level inverter ASD

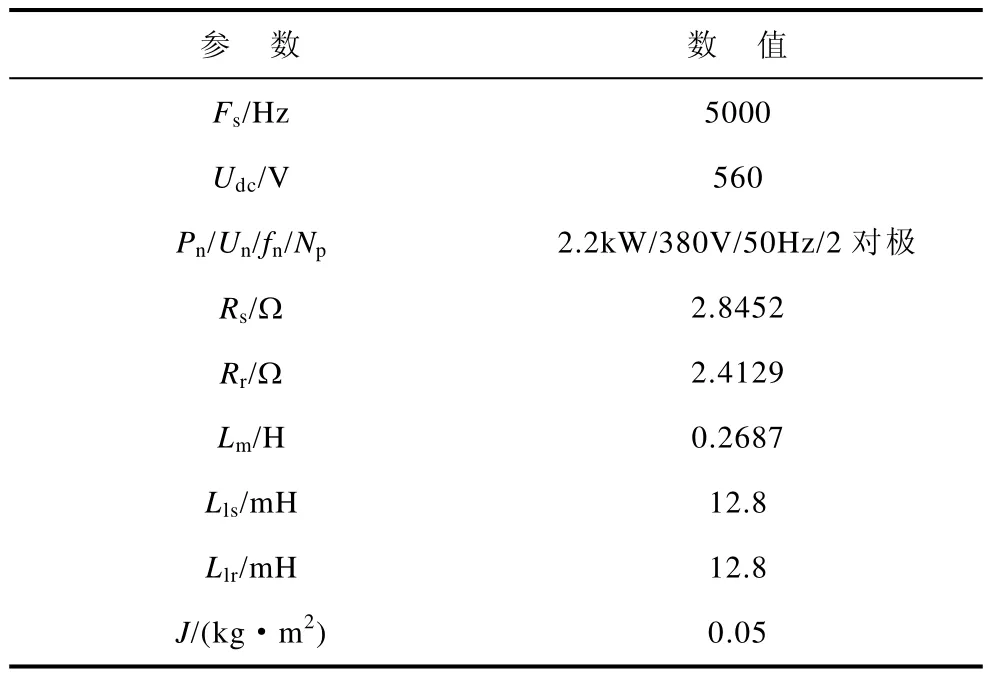
表2 仿真和实验参数Tab.2 Simulated and experimental parameters

进一步在实际三电平变频调速平台上进行了实验，控制系统采用自行研制的以DSP2812为核心的数字化电机控制开发板。所有内部变量如电机转速和磁链、转矩均通过DSP板子上外扩的4通道DA输出，电压和电流则通过探头测得。

首先通过不同工况条件下的实验对转速和磁链环都采用 PI和采用 FLC的性能进行了对比。图 6是电机从静止到 1500r/min的空载起动波形，转速指令值为阶跃信号，采用预励磁技术[9]，在磁通建立后再施加转速指令，可以保证较大的起动转矩而又不致引起过大的起动电流。从图6a中可以看出采用PI有8%的超调，而采用FLC的超调量只有0.9%。图7是低速 15r/min稳态时的波形对比，由于是估计转速进行反馈，从图中估计转速波形可以看出FLC的稳态精度较高，波形比较平滑，而采用 PI的速度波形波动较大。采用FLC的另一个优点是对负载干扰具有较强的鲁棒性，图8考察了PI和FLC在突加负载时的抗干扰性能。当电机稳定运行在空载1500r/min时，突加60%额定负载，从图8a可以看出采用PI控制器时，转速出现了跌落，需要经过较长时间才会恢复到原来稳态，而图 8b表明采用FLC在转速稍微跌落后马上恢复到原来的稳态，表现出极强的抗干扰能力，证明了FLC的强抗负载干扰能力。从图 6～图 8的实验结果可以看出，采用FLC后系统性能尤其是动态性能得到较大改善。

其次，图 9对采用传统转速自适应磁链观测器[6-7]和本文采用新型增益矩阵和转矩观测的观测器进行了对比。电机从反转 1500r/min运行至正转1500r/min，从图 9a可以看出采用传统观测器时在转速过零点磁链和转矩都出现了波动，而且转矩要过较长时间才进入稳态，而采用本文的新型观测器后，图9b表明磁链和转矩在过零点波动很小，而且转矩快速进入稳态，证明引入转矩观测后动态性能得到了提高。

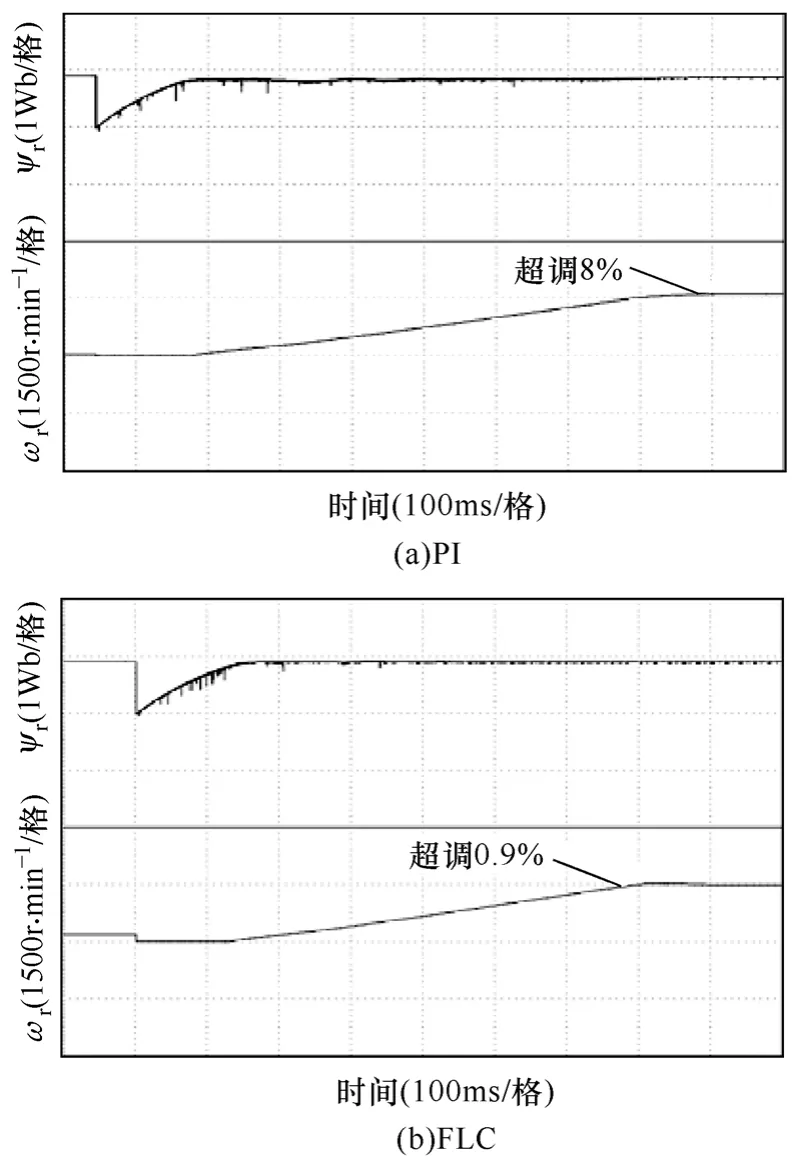
图6 0～1500r/min空载起动波形Fig.6 Starting response from 0 to 1500r/min without load

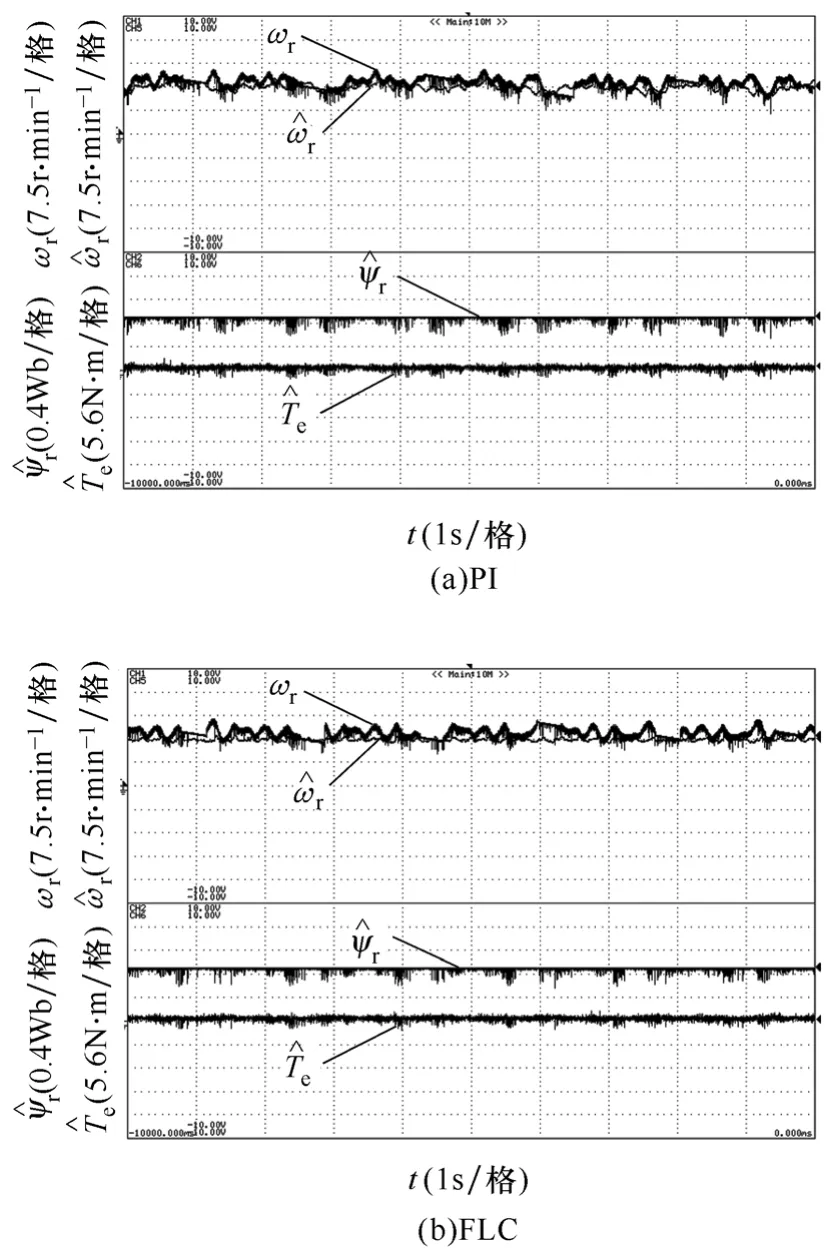
图7 电机15r/min空载稳态波形Fig.7 Steady state motor at 15r/min without load

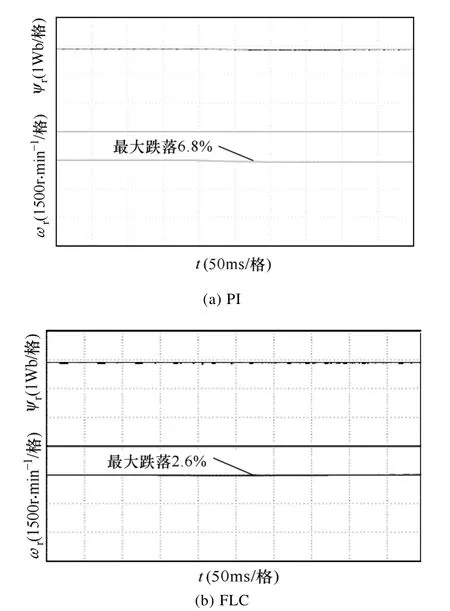
图8 电机1500r/min突加60%负载波形Fig.8 Response to step load change of 60% load of motor at 1500r/min

图9 电机1500r/min正反转波形Fig.9 Reverse to forward operation at 1500r/min

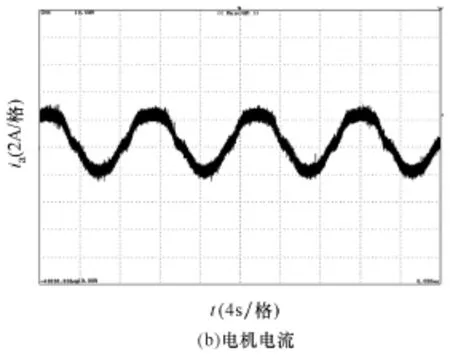
图10 电机3r/min空载稳态波形Fig.10 Steady state motor at 3r/min without load

最后本文还考察了低速时系统的性能。图 10给出了电机在3r/min（0.1Hz）空载稳态运行时的波形，磁链基本恒定不变，估计转速可以较好跟踪实际转速，尽管转子磁链和转速上出现了一些毛刺，定子电流依然比较正弦，可以长时间稳定运行。另外，本文还考察了低速带载性能。图11是电机稳定运行在15r/min，并且带额定负载时的波形。从图中可以看出，即使在低速下，估计转速和实际转速也十分接近，证明本文的观测器在低速带载下也有较好的性能。

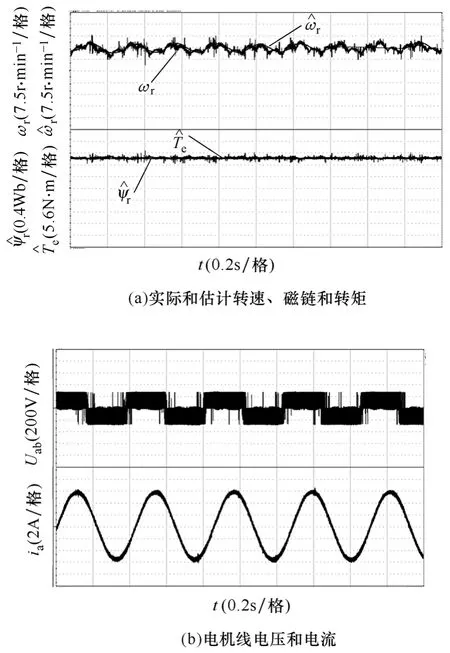
图11 电机15r/min满载稳态波形Fig.11 Steady state motor at 15r/min with 100% rated load

5 结论

本文深入研究并提出了一种简化的自适应观测器增益矩阵选择方法，可以降低系统计算量和估计转速误差的影响，同时改善观测器的稳定性；进一步在观测器中引入转矩观测器，提高了速度估计的动态性能。在转速和磁链调节中采用模糊控制，与传统PI控制器相比，提高了系统的动静态性能和抗负载干扰能力；采用查表和线性插值的方法实现模糊控制，系统具有较强的实时性。实验结果表明，将模糊控制和自适应观测器用在直接矢量控制中，提高了系统的动静态性能，系统在高速和极低速都可以稳定运行，是一种性能优异的无速度传感器控制方案。

[1]Bose B K. 现代电力电子学与交流传动[M]. 北京:机械工业出版社, 2006.

[2]Holtz J. Sensorless control of induction machineswith or without signal injection[J]. IEEE Trans. on Ind. Electron., 2006, 53(1): 7-30.

[3]Schauder C. Adaptive speed identification for vector control of induction motors without rotational transducers[J]. IEEE Trans. on Ind. Appl., 1992,28(5): 1054-1061.

[4]Peng F Z, Fukao T. Robust speed identification for speed sensorless vector control of induction motors[J].IEEE Trans. on Ind. Appl., 1994, 30(5): 1234-1240.

[5]邹旭东, 朱鹏程, 康勇, 等. 基于电压解耦原理的感应电机无速度传感器矢量控制[J]. 中国电机工程学报, 2005, 25(14): 98-102.Zou Xudong, Zhu Pengcheng, Kang Yong, et al.Speed sensorless for vector control of induction motor with voltage decoupling control principle[J]. Proceedings of the CSEE, 2005, 25(14): 98-102.

[6]Kubota H, Matsuse K, Nakmo T. DSP-based speed adaptive flux observer of induction motor[J]. IEEE Trans. on Ind. Appl., 1993, 29(2): 344-348.

[7]Yang G, Chin T H. Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter-induction motor drive[J]. IEEE Trans. on Ind.Appl., 1993, 29(4): 820-825.

[8]Jehudi Maes, Jan A Melkbeek. Speed-sensorless direct torque control of induction motors using an adaptive flux observer[J]. IEEE Trans. on Ind. Appl.,2000, 36(3): 778-785.

[9]张永昌, 赵争鸣, 张颖超, 等. 基于全阶观测器的三电平逆变器异步电机无速度传感器矢量控制系统[J]. 电工技术学报, 2008, 23(11): 34-40.Zhang Yongchang, Zhao Zhengming, Zhang Yingchao,et al. Sensorless vector control system of induction motor fed by three-level inverter using a full order observer[J].Transactions of China Electrotechnical Society, 2008, 23(11): 34-40.

[10]Uddin M N, Radwan T S, Rahman M A. Performances of fuzzy-logic-based indirect vector control for induction motor drive[J]. IEEE Trans. on Ind. Appl.,2002, 38(5): 1219-1225.

[11]Brian Heber, Xu Longya, Tang Yifan. Enhanced speed control of an indirect Fuzzy logic fie1doriented of induction machine drive[J]. IEEE Trans.on Power Electron, 1997, 12（5）: 772-778.

[12]洗成瑜, 王明渝, 刘和平. 基于多模糊控制器的感应电动机矢量控制系统实验研究[J]. 电工技术学报,2004, 19(11): 31-35.Xian Chengyu, Wang Mingyu, Liu Heping.Experimental study of vector control induction motors based on full fuzzy controllers[J]. Transactions of China Electrotechnical Society, 2004, 19(11): 31-35.

[13]Holtz J. The representation of AC machine dynamics by complex signal flow graphs[J]. IEEE Trans. on Ind.Electron., 1995, 42(3): 263-271.

[14]Celanovic N, Boroyevich D.A comprehensive study of neutral-point voltage balancing problem in threelevel neutral-point-clamped voltage source PWM inverters[J]. IEEE Trans. on Power Electron., 2000,15(3): 242-249.

[15]张永昌, 赵争鸣. 基于快速SVM算法的多电平逆变器电容电压平衡问题研究[J]. 中国电机工程学报,2006, 26(18): 71-76.Zhang Yongchang, Zhao Zhengming. Study on capacitor voltage balance for multi-level inverter based on a fast SVM algorithm[J]. Proceedings of the CSEE, 2007, 26(18): 71-76.