带跳跃的分数布朗运动的经济模型

宋燕燕，王子亭

(中国石油大学 数学学院，山东 青岛 266555)

0 引言

在过去的几十年里，大量的学者研究发现金融市场是无套利的，并且遵循一种无规律的随机游走，即布朗运动，给出了期权定价的模型和方法。然而，事实又证明用分数布朗运动代替布朗运动来研究金融市场会更符合实际。文献［1］讨论了一般的跳跃幅度的随机变量和带参数的幂函数为收益函数，但结果并不是很理想，文献［2］讨论了带泊松跳跃的布朗运动的模型，也有一定的局限性。本文具体讨论了跳跃幅度为均匀分布和收益函数为一次多项式的分数布朗运动环境下的经济模型，并且给出一定的限制条件，求得平均收益的最优解。

1 预备知识

设(Ω，F，P)是概率空间，在这个空间上定义如下几个随机过程:

(1)BH=(BHt;t∈R+)，分数布朗运动。

(2)N=(Nt;t∈R+)，参数为λ＞0的泊松过程。

(3)U=(Ut;t∈Z+)，一个独立同分布的均匀分布序列，其中Ui为定义在(-1，1)上的均匀分布。

(4)T=(Tt;i∈Z+)，泊松过程事件发生的时刻序列。

下面，我们定义随机过程X=(Xt;t∈R+):

(1)Xt的初值X0=x。

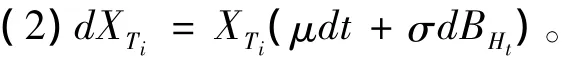
(3)在每次泊松过程事件发生的时刻T=(Ti;i∈Z+)上，Xt在原来的基础上有一个放缩式跳跃XTi=XTi-(1+Ui)，其中XTi-为Xt在Ti的左极限。

2 结论

因此，EXt可分为两部分计算，前者为分数布朗运动的数学期望，后者为泊松跳跃的数学期望。

［1］Masamitsu Ohnishi.An optimal stopping problem for a geometric Brownian motion with Poissonian jumps［J］.Mathematical and Computer modelling，2003，12(38):1381-1390.

［2］王志明，黄志勇，许芳忠.带泊松跳跃的几何布朗运动的经济模型［J］.数学杂志，2007，27(1):93-95.

［3］刘韶跃.数学金融的分数次Black-Scholes模型及应用［D］.长沙:湖南师范大学，2004.

［4］Sudipto Sarkar.The effect mean reversion on investment under uncertainty［J］.Journal of Economic Dynamics and Control，2003，11(28):377-396.