对方案有偏好的三角模糊数型多属性决策方法

张 静

(1.西北师范大学数学与信息科学学院，兰州 730070;2.陇南师范高等专科学校数学系，甘肃 成县 742500)

0 引言

多属性决策是决策理论研究的重要内容，多属性决策问题的研究吸引了国内外很多决策理论专家的兴趣，而且目前它已被广泛应用于投资决策、项目评估、方案评选、人才选拔等诸多领域。由于人们对客观事物认识的主观性、不确定性与模糊性，在实际的决策中经常会出现决策信息的模糊性和不确定性。到目前为止，对指标权重信息完全确知或完全不知的多属性决策问题研究已进行了很多研究，对已知部分权重信息且对方案有偏好的多属性决策人们做过一些研究。本文针对三角模糊数型多属性决策问题，在α截集下引入偏差函数，通过构造目标规划模型求解属性的权重向量，进而求得α截集下方案的排序向量。其次，将不同α截集下的排序向量进行集结，得出方案的综合排序向量。最后根据综合排序向量分量的大小，对方案进行排序择优。该方法充分考虑了主观偏好和客观偏好之间的差异，得出的决策结果具有较好的合理性。

1 预备知识

定义1 若a=［aL，aU］，则称a为一个区间数。特别地，若aL=aU，则a退化为实数。

定义2 设a=［aL，aU］，b=［bL，bU］为两个区间数，则称

定义3 设是定在实数域R上的模糊集合，称为三角模糊数，若的隶属函数为

简记为(l，a，u)，称a为的中心，l与u为的左右展度。当l=u时为正规模糊数。

定义4 设为三角模糊数，满足μa～(x)≥α的所有x构成的集合称为的α截集，记作a(α)=［aL(α)，aU(α)］，其中aL(α)=αa+(1-α)l，aU(α)=αa+(1-α)u。

2 决策方法

对某一多属性决策问题，设方案集X={x1，x2，…，xn}，属性集V={v1，v2，…，vn}，决策矩阵A=()n×m，其中=(lij，aij，uij)是一个三角模糊数，表示方案xi在属性vj下的属性值。为了消除不同属性类型及量纲的影响，将决策矩阵A转化为规范化矩阵R=(r～ ij)n×m。用I1，I2分别表示效益型和成本型指标集，则规范化公式如下:

其中，“∧”为取小算子，L={1，2，…，n}

设w=(w1，w2，…，wm)T为属性的权重向量，H为已知的部分权重信息确定的权重集合，w∈H。决策者对方案xi有一定的主观偏好，设该主观偏好值为三角模糊数(pij)，其中∈［0，1］，j=1，2，3。由于受各种主客观因素的影响，决策者的主观偏好值和客观偏好值之间往往存在一定的偏差。分别对主、客观偏好值做α截集，则在 α 截集下的取值区间为(α)=［(α)，(α)］，p～i在 α 截集下的取值区间为(α)=［(α)，(α)］。引入左、右加权偏差函数:

为了使决策具有合理性，权重向量的选取应该使决策者在α截集水平下的主、客观偏好间的总偏差最小，从而建立优化模型:

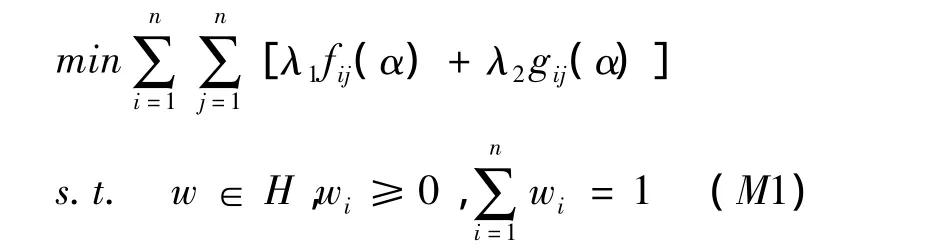
其中，λ1，λ2为左右偏差的权重系数。考虑到偏差函数是公平竞争的，没有任何偏好关系，且希望达到的期望值为零，一般可取λ1=λ2=1。因此，可将上述模型(M1)转化为下列目标规划模型:

利用Lingo软件编程求解模型M2，得到α截集下的属性 权 重 向 量w(α)=(w1(α)，w2(α)，…，wn(α))。根据公式

计算方案xi在α截集下的综合属性值zi(w(α))，其中i=1，2，…，n。由于zi(w(α))为区间数，不便直接进行排序，可由区间数排序的可能度公式，建立截集下各方案综合属性值之间两两比较的可能度矩阵P(α)=［pij(α)］n×m利用公式:

计算α截集下方案的排序向量:

例如，可选取αk=，k=1，2，…，n，n的大小可根据决策者对精度的要求适当选取。

3 算例分析

考核、选拔干部是一个多因素决策问题，决策者一方面要把德才优秀的人才选拔到领导岗位;另一方面，也希望在条件相当的情况下任用自己所偏好的人才。某单位在对干部进行考核选拔时，首先制定了6项考核指标(属性):思想品德(v1)、工作态度(v2)、工作作风(v3)、文化水平和知识结构(v4)、领导能力(v5)、开拓能力(v6)，这些指标均为越大越好型指标。然后由群众推荐、评议，对各项指标分别打分，再进行统计处理，并从中确定了5 名候选人xj(j=1，2，3，4，5)。由于群众对统一候选人给出的指标值(属性值)并不完全相同，因此经过统计处理后的每个候选人在各指标(属性)下的属性值是以区间数形式给出的。具体的属性值如表1。

表1 每个候选人在各项指标下的属性值

已知各项指标的权重信息为:

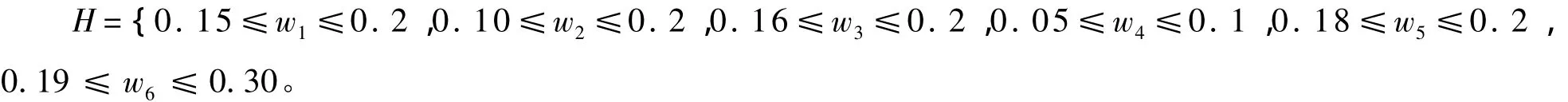
设决策者对5个候选人xj(j=1，2，3，4，5)的主观偏好值分别为:

现用本文所介绍的方法对5个候选人进行排序。具体步骤如下:

首先根据表1中的数据建立模糊决策矩阵A。

根据规范化公式，将A转化为规范化决策矩阵R。

在α截集下三角模糊数矩阵转化为区间数决策矩阵R(α)，当α=0时，

将相关数据代入模型M2，利用lingo软件算出α=0截集下的属性权重向量w(0)=(0.08，0.13，0.15，0.25，0.26，0.13)，再由公式(1)、(3)、(4)计算得α=0时的方案排序向量:σ(0)=(0.1，0.09，0.13，0.27，0.28，0.12)为了便于计算，可选取 αk=，k=0，1，2，…，5，

同理可得:

根据公式(3)，可求得方案的综合排序向量σ=(0.09，0.11，0.16，0.26，0.25，13)，从而方案的最终排序为:x4＞x5＞x3＞x2＞x6＞x1。

4 结束语

本文采用文献［7，8］所提出的三角模糊矩阵规范化方法，对三角模糊数求截集，将三角模糊数转化为区间数，同时引入充分考虑了决策者偏好关系的偏差函数，建立目标线性规划模型并利用Lingo软件求出属性权重向量，进而对截集下的方案进行排序。

［1］许叶军.权重信息完全未知的不确定型多属性决策的一种新方法［J］.运筹学学报，2007，5(11):295-300.

［2］兰继斌，王中兴，霍良安.不确定性多属性决策的新方法［J］.运筹与管理，2006，15(6):48-53.

［3］徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究［J］.系统工程与电子技术，2002，24(8):9-20.

［4］林健.权重信息不完全的梯形模糊数多属性决策方法［J］.重庆工学院学报，2008，22(7):145-152.

［5］徐泽水，达庆利.区间数排序的可能度法及其应用［J］.系统工程学报，2003，18(1):67-70.

［6］李荣钧.模糊多准则决策理论及应用［M］.北京:科学出版社，2000.

［7］徐泽水.不确定多属性决策方法及应用［M］.北京:清华大学出版社，2004.

［8］樊冶平，宫贤斌，张全.区间数多属性决策中决策矩阵的规范化方法［J］.东北大学学报:自然科学版，1999，20(3):326-329.