一种基于RFID原理的交通信息获取系统与车辆定位方法

赵泰洋 郭成安 金明录

(大连理工大学电子与信息工程学院 大连 116024)

1 引言

交通信息获取是实现智能交通系统(ITS)的基础。其中车辆的身份信息和位置信息是交通信息中的关键部分。

当前，应用较广的车辆身份信息获取方法主要包括：基于视频监控车牌图像识别的方法[1]，基于DSRC(Dedicated Short Range Communication 专用短程通信)的方法[2]和基于 RFID 电子标签的方法[3,4]。视频监控车牌图像识别的方法易受环境(如天气)、照明等因素影响，正确率难达到很高。基于DSRC的车辆身份识别方法目前主要用于高速公路不停车收费系统中，其主要优点是身份识别率接近100%，可全天候工作。但由于其设计目的是用于短距离通信，所以该技术常用于某一车道上车辆的身份识别，而不适于某一范围(如交通路口)内所有车辆的身份识别。基于 RFID电子标签的方法采用RFID电子标签作为识别手段，除具备DSRC的优势外，还具有设备成本低、通信距离远的优势，与DSRC技术相比，更适合于车辆身份的识别。

智能交通系统体系框架的 33种用户服务中有20余种与车辆的实时定位有关[5]。因此如何高效、准确的获取车辆的位置信息已成为近年来智能交通领域研究的一个热点。随着研究的深入，人们提出了多种车辆位置信息获取方法。在车辆导航、定位系统中，典型的车辆位置信息的获取方法主要有：基于 GPS与加速度传感器的车辆定位方法[6,7]和基于多基站无线定位的方法[3,4]。前者是一种基于移动站的定位方法，即车载定位设备仅会向车辆的驾驶者提供位置信息。因此车辆还需通过无线通信将得到的位置信息上报给交通管理系统。这种以被定位物体作为主动方获取位置信息的方法具有占用通信资源多，系统运行成本高的缺点。基于多基站无线定位的方法则是以基站作为主动方获取定位信息，通常利用接收信号强度(RSSI)、到达时间(TOA)[7-9]、到达时间差(TDOA)定位。但多基站无线定位方法也存在一些弱点，如定位精度易受周围环境噪声和基站分布等因素影响，因而定位精度不高。

目前已有的多基站定位技术有到达角度(Angle of Arrival，AOA)、到达时间(TOA)、到达时间差(TDOA)、到达相位(POA)、到达相位差(PDOA),到达频率差(FDOA)及以上几种技术的混合定位算法[10,11]。其中TDOA是目前最有发展潜力的定位技术。它已被成功应用于IS-95 CDMA和GSM系统中[12]。

2 基于有源RFID的交通信息获取系统

2.1 交通信息获取方案设计与系统构成

本文基于有源RFID的交通信息获取系统主要实现两个功能：一是获取车辆的身份信息，二是获取车辆的位置信息。

该系统采用基于RFID电子标签的方法获取车辆的身份信息，采用基于TDOA的多基站无线定位方法获取车辆的位置信息。该系统的结构示意图如图1所示，主要包括有源RFID电子车牌，用于与电子车牌通信和获取车辆身份信息和位置信息的基站及用于数据处理和交通管理的管理中心3部分[3]。

图1 基于RFID技术的交通信息获取系统示意图

在该系统中，每个车辆均装配一个电子车牌。该电子车牌是一个有源RFID装置，其中存储有该车辆的身份信息(如车牌号码等)。

基站通常设置于路口或路边，既可获取车辆身份信息，又可获取车辆位置信息。图2是基站的功能框图。该基站由有源RFID信息获取单元、无线定位发射机、无线定位接收机、数据处理单元、中央控制单元、网络通信单元和GPS模块构成。中央控制单元负责基站所有任务的管理。有源RFID信息获取单元用于获取车辆的身份信息，它可与在基站附近通过的电子车牌进行通信。电子车牌在接收到RFID信息获取单元发来的信号后发射自己的身份信息，以此实现车辆的身份识别。有源RFID信息获取单元的通信覆盖范围称为通信覆盖范围(半径约为100 m-200 m)。基站中的无线定位发射机可发射功率在一定范围内可调的射频信号，启动处于其定位覆盖范围(半径约为3000 m-5000 m)内的电子车牌，通过采用专门设计的搜索定位算法来实现目标的定位。无线定位接收机具有较高的灵敏度和较低的噪声系数，可接收到定位覆盖范围内的电子车牌发射的微弱的射频信号，并对该信号进行滤波、放大等处理。数据处理单元对无线定位接收机输出的信号进行分析，估计信号的到达时间，进而估计车辆与该基站的直线距离。

图2 基站功能框图

分控中心是市区中某个地区智能交通系统的控制中枢，负责处理基站发送过来的各种信息，如车牌号码、车辆与基站距离等信息。一个城市可以有多个分控中心，也可以只设一个分控中心。有多个分控中心的场合，还应设有总控中心，来集中管理各个分控中心。

2.2 车辆身份信息获取子系统通信方式

如前所述，通信基站通常被设置在路口附近，获取驶入其通信覆盖范围的车辆的身份信息。当有多个车辆同时驶入其通信覆盖范围时，为了防止多个电子车牌同时向基站发送身份信息造成相互干扰，本系统采用基于分时隙ALOHA的时分复用通信协议[3]。基站向处于其通信覆盖范围内的电子车牌发送同步指令，各个电子车牌接到指令后随机选择一个上行时隙向基站发送身份信息。当其收到基站的确认信号后，进入休眠状态，不再与基站通信。若没有收到基站的确认信号，则在下一次收到同步指令后，再次随机选择一个上行时隙向基站发送身份信息。直到收到基站的确认信息为止。采用这种通信方式即节省频率资源，又可有效地解决通信碰撞问题。

各通信基站与分控中心，以及分控中心与总控中心通过专用网络进行通信。通信协议采用成熟的TCP/IP协议。

3 多基站二次鲁棒性定位方法

本文采用基于TDOA的定位技术，文献[13,14]中详细讨论了传统的多基站TDOA技术，并给出了Chan算法的推导过程。在文献[13]中Chan算法的推导是在 TDOA误差较小且服从正态分布的假设下进行的。在基站数大于3时，采用了近似的方法。随着TDOA误差的增加，近似不再成立，此时定位精度会迅速降低。

下文以 7基站为例研究多基站定位问题。图 3是本文所研究的交通信息获取系统中定位基站与待定位车辆的意示图，图中BS0到BS6代表7个基站，其位置坐标已知。MS是车辆所处的位置。

由于待定位车辆与各基站间的距离不等，车辆发射的电磁波到各个基站的衰减有所不同，这会造成各个基站接收到信号的信噪比不同，最终导致信号的到达时间差(TDOA)的分布不同。若直接使用BS1到BS6 6个基站相对于BS0的TDOA值对待定位车辆采用经典 Chan算法进行定位，由于各个TDOA估值精度相差很大，会产生较大的定位误差。如果能先设法找到估值误差最小的两个TDOA值(3基站)用于最后定位，则会显著改善定位效果。因为TDOA值的估计精度与接收信号的信噪比有关，而接收信号的信噪比又与信号的传播距离有关，所以只要找到与待定位车辆距离最近的3个基站，也就找到了估计精度最高的两个TDOA值。

图3 7基站定位示意图

根据这一思路，本文提出一种基于鲁棒性估计的多基站车辆定位方法。该定位方法分成两个步骤：首先利用7个基站的全部信息采用鲁棒性估计方法对车辆进行粗定位，从中找到距其最近的3个基站，然后利用这3个基站的时延估计信息对车辆再做进一步定位，以提高精度。

由文献[13,14]的推导可知，在多基站定位方法中，采用3基站定位，误差的影响相对较小。所以在第1步的粗定位过程中，采用3基站的定位方法。在图3中，共有7个基站。在这7个基站中，任选3个基站用于3基站定位，共有35种(组合。每种组合都会得到一个定位结果。而我们事先并不知道哪些基站距离更近些，因此并不知道哪些定位结果较为精确。如何由这35个定位结果得到真实位置的较精确的估计呢？一种简单的处理方法就是对35个 3基站定位结果中的横坐标和纵坐标分别求均值，以此作为粗定位的结果。但该方法对所有的35个结果一视同仁，不能十分有效地减小定位误差。鲁棒性估计是一种抗异常干扰(Outliers)的统计方法[14]，本文采用Huber的鲁棒性M估计来解决该定位问题。根据该领域已有的工作[14,15]，本文采用式(1)的方法来实现M估计。

式中N=35，xi是第i组定位结果中的横坐标，表示35个定位结果中横坐标的平均值，s表示定位结果的横坐标的标准差。CH称为调节常数，这里为2，β取0.921。对于纵坐标Yi的估计，则采用完全类似的方法来处理，此处不再赘述。

式(1)中N'和N''分别是满足式(3)和式(4)的xi的个数。

利用和作为迭代初值，按照迭代公式(1)进行迭代，通常迭代两次即可得到较满意的结果。

利用上述鲁棒性估计方法得到移动目标(电子车牌)的位置估值后，采用简单的比较判断法即可得到距离当前目标最近的 3个基站。然后再利用这3个基站的TDOA信息，进一步采用3基站的Chan算法，对电子车牌进行第2步的定位运算，以此作为对目标的最终定位结果。

虽然该定位过程分为两个步骤，但这两步估计所用到的 TDOA数据是在同一次通信过程中得到的。因此两步估计法并不会增加电子车牌与基站通信的次数，并不增加额外的通信开销。

4 实验结果举例与分析

针对本文的RFID交通信息获取系统和多基站鲁棒性定位方法，本文进行了大量的仿真实验。在实验中，电子车牌发射的信号频率为315 MHz, 发射功率为10 dBm。仿真实验中基站与待定位车辆的位置如图3所示，采用COST-231-HATA模型[16]计算信号的衰减。表1列出了电子车牌发射的信号到各个基站的衰减。

表1 电子车牌发射的信号到各个基站的衰减

从表1中可见，各个基站接收到的信号衰减相差很大，因此各个基站接收到信号的信噪比也相差很大，所以不能用同一个信噪比来衡量不同基站处的信号强度。在本文中，假定各个基站处的噪声功率是相同的，可以采用背景噪声功率来描述该定位系统所处的环境。

车辆发射的信号到基站的 TOA估计采用自适应滤波时间延迟估计(LMSTDE)方法。之后再将两个基站得到的 TOA估计相减即可得到两基站的TDOA。在定位实验开始前，先在5种不同功率的背景噪声的环境下进行TDOA估计的仿真实现，每种背景噪声环境下进行100次仿真实验，最终得到一个由500组TDOA值构成的数据文件。之后的每次定位实验都使用同一个数据文件。

图4是一次典型的仿真实验结果。此次实验中，环境噪声功率为-107 dBm。图中大部分三基站的定位结果分布于实际位置的周围，少数距离实际位置较远。第1步的鲁棒性估计结果的误差要比直接用7基站Chan算法的定位误差小很多。

本文对两种经典的 Chan算法的性能进行了仿真实验。第1种方法利用与待定位车辆距离最近的BS0、BS1和BS2 3个基站对其进行定位，此时采用经典的3基站定位算法；第2种方法采用全部7个基站对车辆进行定位，此时采用经典的多基站定位算法。表2中的数据是不同噪声功率下两种方法定位误差的平均值。

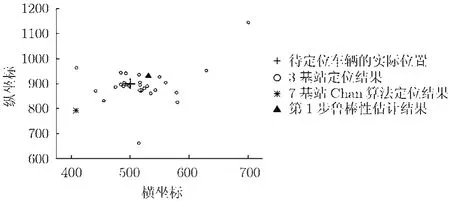
图4 噪声功率为-107 dBm时几种定位方法的定位结果

表2 3基站Chan方法和7基站Chan方法定位结果比较

从表2的数据可见，当噪声功率大于-110.1 dBm时，3基站定位方法性能要远好于7基站定位方法。这是因为在这7个基站中，距离待定位车辆较远的几个基站得到的TDOA值存在很大的误差，近似不再成立，所以导致多基站算法的性能随着背景噪声功率的增加急剧下降。

然而，对于实际的定位问题，我们事先并不知道哪些基站与目标距离近，哪些基站与目标距离远，需要采用某种方法来获取这种信息。本文采用前述的鲁棒性估计方法来解决此问题。为此，本文进一步对3种不同的粗定位方法在不同背景噪声下进行仿真实验，考查其定位性能。第1种方法采用7个基站间的6个TDOA值，利用经典的多基站Chan算法对车辆进行定位；第2种方法将35个3基站定位结果进行平均，用均值作为粗定位的结果；第 3种方法采用本文提出的鲁棒性估计方法对35个3基站定位结果进行处理，经两次迭代得到定位结果。表3中的数据是不同噪声功率下3种方法定位误差的平均值。

表3 3种方法进行粗定位的仿真结果

从表3中的结果可见，平均法在噪声功率较高时优于7基站定位法。而鲁棒性估计方法在噪声功率较高时又优于7基站定位法和直接平均法。在噪声功率较低时，鲁棒性估计法的平均误差比直接定位法略大。这实质上体现了鲁棒性估计的特点：当信号的统计模型严重变差时，估计性能不至于严重变差；当实际的统计模型与假定的理论模型一致时，估计性能良好，但达不到某种准则下的最佳性能。因为在实际定位问题中，事先并不知道哪些基站离待定位目标近，哪些离待定位目标远，也不能准确得知哪些基站受噪声干扰较大，因此采用鲁棒性估计方法更为可靠一些。为了进一步提高定位精度，本文采用2次定位措施。即在第1步的粗定位(鲁棒性定位)基础上，选择与目标最近的3个基站，利用其TDOA值采用Chan方法进行第2次定位。由于第1步的粗定位是第2步精确定位的基础，若粗定位的误差较大，会直接影响第2步基站的选择。从实验结果来看，虽然在背景噪声功率较低时，鲁棒性估计法的定位误差略大于7基站经典Chan算法的定位误差，但这种误差不会对第2步中基站选择造成太大的影响；而当噪声功率较高时，鲁棒性估计法的平均误差要显著优于其它两种方法，这对于抗强噪声干扰是十分有利的。

本文针对这种基于鲁棒性估计的2步定位法进行了深入实验。在实验中，采用两种方法进行第 1步的粗定位：第1种采用鲁棒性估计方法；第2种是使用直接平均法。在第1步定位估计的基础上，再进行第2步精定位。第2步定位都是采用与待定位车辆距离最近的3基站定位。表4中的数据是不同噪声功率下两种方法的第1步和第2步定位误差的平均值。

从表4的结果可见，在噪声功率较低的情况下(处于-116.8 dBm～-113.6 dBm之间时)，虽然两种方法在第1步粗定位中的性能有所不同，但并不影响第2步中基站的选择，最终两种方法的第2步估计结果完全相同。而当噪声功率较大时(处于-110.1 dBm～-103.7 dBm之间)，不论是第1步粗定位误差还是第2步精确定位误差，鲁棒性估计2步法都要远优于基于直接平均的2步法。

图5是在不同噪声功率下7基站Chan算法和本文的基于鲁棒性估计的2步定位法实验结果的比较。从图中可见，本文的基于鲁棒性估计的2步法的性能显著优于7基站Chan算法的性能，也优于1步鲁棒性估计方法(第 1步粗定位)。在背景噪声为-103.7 dBm，定位半径为3000 m时，本文的基于鲁棒性估计的 2步定位法的平均估计误差约为200 m，相对误差为6.7%，可以满足智能交通系统中机动车辆定位的要求。

5 结束语

表4 鲁棒性估计两步法定位结果

本文提出了一种基于RFID技术的交通信息获取系统，在此基础上提出一种多基站车辆定位方法。该方法是一种基于鲁棒性估计的两步定位方法。在第1步估计过程中，针对基站与待定位车辆距离较远时，由于信号衰减和噪声干扰造成的TDOA估计误差过大的问题，采用鲁棒性估计方法，可以减小其对估计值的影响。然后，在第1步估计的基础上，找到与电子车牌距离最近的3个基站，应用这3个基站的TDOA值进行第2次定位。本文对所提出的交通信息获取系统和车辆定位方法进行了大量仿真实验，结果表明，这种基于鲁棒性估计的2次定位法在多基站无线定位上要显著优于传统的 Chan算法，也优于基于直接平均的2次定位法，可满足交通信息获取系统中对机动车辆定位的要求。

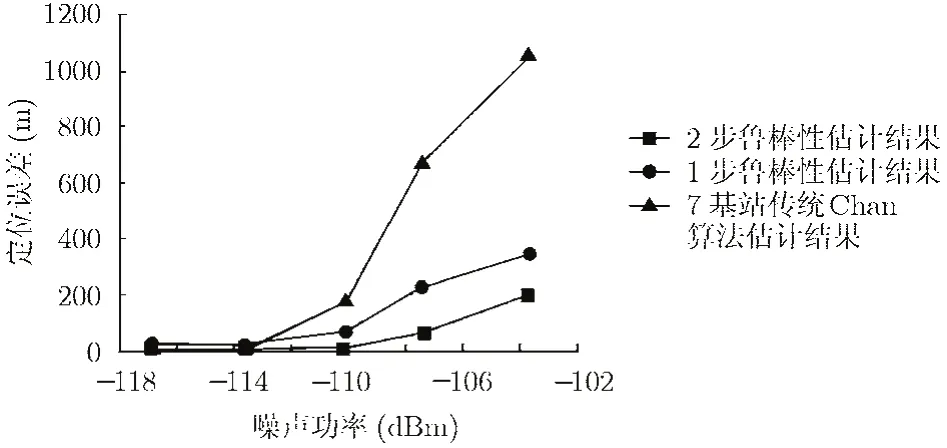
图5 不同定位方法的实验结果性能曲线

在本文的机动车辆定位方法中，是在假设可以获得有效的TDOA值基础上设计的。虽然现在已有较为成熟的TDOA估计方法，但在信噪比较低情况下，如何获得可靠的TDOA估值存在一定的问题。因此为了妥善解决本文的机动车辆定位问题，还需要深入探讨在信号衰减和噪声干扰均较为严重的条件下的时延估计问题。同时，在本文的2次鲁棒性定位方法中，需要求解多个3基站的定位估值(对于7基站参与定位情况，需要求解35个3基站定位估值)。对于有实时性要求的机动车辆定位问题，该项计算是不容忽略的。因此，如何开发快速定位算法，提高计算效率也是本文工作的进一步研究方向。

[1] Hamey L G C and Priest C. Automatic Number Plate Recognition for Australian Conditions [C]. Digital Image Computing Techniques and Applications, Queensland,Australia, 2005: 14.

[2] Wolfgang D and Wilhelm G. Interoperable 5.8GHz DSRC system as basis for European wide ETC implementation [C].European Microwave Conference, Jerusalem, 1997, 1:139-145.

[3] 赵泰洋. 一种动态交通信息获取系统的设计与实现 [D]. [硕士论文]，大连: 大连理工大学, 2006.Zhao Tai-yang. Design and implementation of a dynamic traffic information acquisition system[D]. [MA. dissertation],Dalian: Dalian University of Technology, 2006.

[4] 刘保卫. 基于RFID原理的交通目标搜索与定位技术研究 [D].[硕士论文], 大连: 大连理工大学, 2007.Liu Bao-wei. Search and location of transportation targets based on RFID [D]. [MA. dissertation], Dalian: Dalian University of Technology, 2007.

[5] 傅常伦. 基于车辆定位系统的数据融合及其在城市交通中的应用[D]. [硕士论文], 上海: 同济大学, 2008.Fu Chang-lun. The data fusion based on Automatic Vehicle Location System and its application in Urban Traffic[D]. [MA.dissertation], Tongji University, 2008.

[6] Iqbal U, Okou A F, and Noureldin A. An integrated reduced inertial sensor system- RISS/GPS for land vehicle [C].Position, Location and Navigation Symposium, Monterey,Canada, 2008: 1014-1021.

[7] Guvenc I and Chong Chia-Chin. A survey on TOA based sireless localization and NLOS mitigation techniques[J].IEEE CommunicationsSurveys&Tutorials, 2009, 11(3):107-124.

[8] Jiao Lei, Xing Jian-ping, and Li F Y. Performance comparison of residual related algorithms for ToA positioning in wireless terrestrial and sensor networks[C]. VITAE 2009.1st International Conference, Aalborg, Denmark, 2009:278-283.

[9] 杨天池, 金梁, 程娟. 一种基于TOA定位的CHAN改进算法[J]. 电子学报, 2009, 37(4): 819-822.Yang Tian-chi, Jin Liang, and Cheng Juan. An improvement CHAN algorithm based on TOA position[J].Acta Electronica Sinica, 2009, 37(4): 819-822.

[10] Wang Zhong-hai and Zekavat S A. A novel semidistributed localization via multinode TOA–DOA fusion [J].IEEE Transactions on Vehicular Technology, 2009, 58(7):3426-3435.

[11] Mallat A and Vandendorpe L. CRBS for the joint estimation of TOA and AOA in wideband MISO and MIMO Systems:Comparison with SISO and SIMO systems [C]. IEEE International Conference on Communications, Bresden,Germany, 2009: 1-6.

[12] 张令文，谈振辉. 基于泰勒级数展开的蜂窝TDOA定位新算法[J]. 通信学报, 2007, 28(6): 7-11.Zhang Ling-wen and Tan Zhen-hui. New TDOA algorithm based on Taylor series expansion in cellular networks[J].Journal on Communications,2007, 28(6): 7-11.

[13] Chan Y T. A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing, 1994,42(8): 1905-1915.

[14] 高建立. 基于RFID与DSP技术的车辆定位算法研究 [D]. [硕士论文], 大连: 大连理工大学, 2008.Gao Jian-li. Study on location algorithm of vehicle based on RFID and DSP [D]. [MA. dissertation] Dalian: Dalian University of Technology, 2008.

[15] 王宏禹，郭成安. AR模型的韧性(Robust)估计——GM估计方法[J]. 通信学报, 1987, 8(2): 1-9.Wang Hong-yu and Guo Cheng-an. Robust estimation of AR models – the GM estimation method [J].Journal of China Institute of Communications, 1987, 8(2): 1-9.

[16] Hata M. Empirical formula for propagation loss in land mobile radio services [J].IEEE Transactions on Vehicular Technology, 1980, 29(3): 317-325.