基于原型图的低码率LDPC码最小和译码算法改进方案

姜 明 王 晨

(东南大学移动通信国家重点实验室 南京 210096)

1 引言

低密度奇偶校验(Low-Density Parity-Check，LDPC)码[1]具有接近香侬限的性能，已有的研究结果表明精心设计的非规则 LDPC码长码[2]能逼近信道容量极限，性能优于turbo码。在低信噪比下，高码率的码字译码性能较差，甚至无法译码，而低码率码字可以在低信噪比下有较好的译码性能。由于根据同一个原型图构造出来的任意长度LDPC码都有相同的基本结构，通过密度演变算法或外部信息转移(Extrinsic Information Transfer Charts,EXIT)图[3]分析计算原型图的门限值，可以方便的预测基于当前原型图构造出的码字性能，同时，原型图构造的码字的门限逼近信道容量。

在LDPC码的软判决译码算法中，置信传播(Belief Propagation，BP)算法性能最好，但其在校验节点计算时涉及大量的对数和指数运算，计算复杂度大，译码时延长。尽管关于LDPC码的译码算法研究，在硬判决[4,5]和软判决[6,7]方面有许多新成果，但改进的最小和(Min-Sum, MS)算法[8]在译码性能和实现复杂度上仍有较为明显的优势。MS算法在校验式更新计算方面进行了简化处理，但该近似算法的性能与BP算法相比还存在一定的差距，通过归一化的最小和算法(Normalized Min Sum，NMS)进行修正，性能与MS相比得到提高，复杂上远远小于BP算法，是一种较好的折中处理方案。

原型图构造的LDPC码[9]的校验矩阵行重差异较大，通常有超轻的行重和列重。对于该类码字若采用普通的NMS修正误差较大，所以NMS算法在此类码字上的译码性能有较大损失。因此本文提出在NMS迭代译码算法中结合震荡抵消(Oscillation,OSC)处理[10]和多系数(Multiple Factors，MF)[11]修正技术，改进NMS算法对基于原图的低码率LDPC码的译码性能。OSC处理和MF修正技术硬件实现简单，与标准的NMS算法相比，增加的译码复杂度和译码处理时延几乎可以忽略不计。

本文结构如下：首先简单描述基于原型图构造的低码率LDPC码，接着介绍Min-Sum算法及改进方案，然后阐述NMS算法结合震荡抵消处理，以及针对不同的行重采用多系数修正的改进方案，最后给出对低码率原型图码字的仿真结果并给出结论。

2 低码率原型图

Divsalar在文献[12]中提出基于原型图的低码率LDPC码码字构造，我们首先简单介绍其中AR4A和ARJA两类原型图。图1是基于AR4A原型图构造的1/3码率的LDPC码，原型图中4个圆形●和○节点为比特节点和3个⊕形节点为校验节点，其中○节点表示要打孔的比特节点。右边的两个比特节点和两个校验节点相连形成累加器。左边的验节点和度数为1的比特节点可以用多个这样的校验-比特节点对来代替，从而进一步得到更低码率的LDPC码。基于原型图的EXIT分析可以算出图1扩展出的LDPC码其迭代译码门限为0.005 dB。

AR4A码的原型图中，度数为2 的比特节点数较多，占到50%的比例，而且这两个节点之间无直接关联。如果用度数3的比特节点代替一个度数为2的比特节点，并且增加这两个节点间的关联，可以有效改善低码率码字的误码率平层(error floor)效应。按照上述方法构造的码字称为ARJA 码，如图2所示。从图中可以看出，基于ARJA原型图构造的1/4码率LDPC码，包含有9个比特节点和7个校验节点，其中一个比特节点做打孔处理。

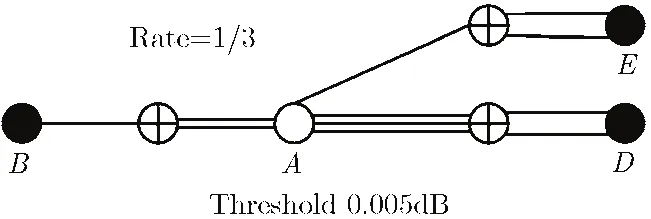
图1 1/3码率AR4A原型图

图2 1/4码率的ARJA原型图

从图1和图2可以看出，原型图码字尤其是低码率原型图和常规的非规则LDPC码不同，不仅比特节点存在不同的重量分布，其校验节点重量也有较大差异。例如AR4A原型图中1/3的校验节点重量为5，2/3的节点重量只有3，ARJA原型图中的校验节点有6，4，3三种重量。标准的NMS译码算法对不同重量的校验节点都采用相同的修正因子，而当重量差异较大时，这样的修正将会带来一定的性能损失。

3 Min-Sum算法及改进方案

基于似然比(LLR)域的BP算法中校验节点的计算如式(1)，其中涉及到大量的加法，乘法，对数以及指数运算，运算复杂度较大。对BP算法的校验节点计算单元做简化处理，是降低BP算法运算复杂度的一个有效途径。最小和算法是针对这一问题，通过简化校验节点的计算，降低了复杂度,校验节点的计算如式(2)所示，其中R和Q分布表示校验节点向比特节点输出的更新信息和比特节点向校验节点的输入信息。

MS算法中的校验节点计算单元采用近似方法计算，有效地降低了校验节点的计算复杂度，原先BP算法中的指数和对数运算被简单的比较运算所取代。在节点重量相同的条件下，MS算法中校验节点和比特节点的计算复杂度近似相等。虽然MS算法的复杂度明显低于BP译码算法，但简化处理也使得其译码性能相比BP算法有较大的差距。BP算法的校验节点输出信息可靠度大小应当略小于MS 算法的输出幅值。所以如果要很好地逼近标准输出结果，必须适当降低MS近似输出信息的绝对值大小。

文献[3]给出了修正的MS算法，不考虑校验式的其他输入信号大小，直接对校验式输出的最小值数据作修正。其中最简单的归一化修正如式(3)，通过一个乘性因子α修正MS算法校验式输出，即NMS算法。式中的α可以取0到1之间不同值，对应的性能也会有差别。

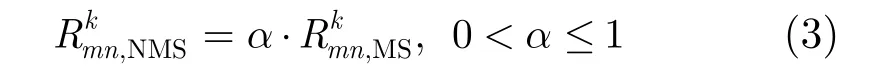
另外一种改进对MS算法的改进就是线性近似算法。在BP算法中，校验节点的计算公式在硬件实现上非常困难和复杂，需要查表、额外的空间。文献[13]提出一种线性近似的拟合方案，BP算法中校验节点计算公式(1)中的对数项被近似为线性函数式(4)。通过密度演变等算法可以确定，式(4)中当m=0.24，t=0.6时性能最佳，与采用精确计算的BP算法的性能几乎相同。通过线性近似，BP算法中校验节点计算的对数、指数运算变成乘法、加法运算，运算复杂度大大降低。虽然线性近似的性能与BP差距很小，但是其译码复杂度还是要明显大于MS类算法。

4 震荡抵消和因子优化选取

LDPC译码过程中一般存在3种错误：译码收敛到一个不满足校验方程的伪码(pseudo codeword)，或各比特节点的APP-LLR(A Posteriori Probability， APP-LLR)处于震荡不能收敛到一个固定状态，还有就是译码收敛到一个满足校验方程的错误码字，即不可检验错误。当某些比特的APP-LLR在迭代过程中发生震荡，该状态将通过校验节点蔓延到其他比特节点。因此，在每次迭代时错误比特的位置和数量都在不断发生变化，码字无法收敛，无法获得正确的码字，尽管迭代一直在进行并达到最大迭代次数。为了对抗这种现象，在最小和算法中可以采用震荡抵消(OSC)[10]技术，对比特节点迭代过程中输出外信息LLR值做修正。

首先我们将比特节点向校验节点传递的LLR外信息的符号翻转作为OSC处理的判断准则。如果输出外信息出现符号变化，则减弱该条边上的传递的输出信息可靠度，新的幅值将变小，并赋予和幅值较大的相同的符号，若符号不变，则继续使用更新的LLR输出信息。迭代过程中修正步骤具体执行如式(5)。无论是BP算法还是MS算法，其迭代处理过程可以通过式(5)很有效地区分处理迭代译码中正确信息和错误信息的传播。将震荡处理应用在NMS算法中，误码率性能改善相当明显。

对于NMS算法，如果对所有的校验节点采用单一修正因子α时，尤其对于低码率码字，修正效果并不理想。在文献[14]中，对不同码率和不同分布的LDPC码，给出了通过密度演变算法分析校验节点最佳修正因子的方法。具体如常规的(3,6)分布1/2码，其校验式修正因子大致取到0.8左右，随着码率的升高，校验式重量增加，但最优的修正因子也逐渐稳定在0.8附近。但对于低码率，尤其是基于原图的这类低码率编码，其校验矩阵存在重量超轻的校验节点，对应的最佳修正因子数值一般在0.8到1之间。依据上述原因，我们再结合多系数(MF)修正技术[11]，对基于原图构造的一类低码率LDPC码校验矩阵中不同重量的校验式，采用不同的修正因子，从而取得更好的译码性能。

在译码复杂度方面，无论是OSC处理和MF修正技术，其硬件实现都很简单。与标准的NMS算法相比，MF修正只是针对不同的检验单元预设不同的修正因子，没有增加译码实现复杂度。而OSC处理，只是在变量节点的更新处理单元部分，增加了一个简单的符号相乘判决，然后依据符号对存储单元做直接存储或累加存储，相应增加的硬件复杂度几乎可以忽略不计。

5 仿真结果

首先本文采用图1中的1/3码率的AR4A原型图，构造了一个低码率LDPC码，并对该码字进行仿真实验，得到对应的误码率仿真结果，如图3。原形图中共有4个变量节点，3个校验节点，其中一个变量节点被打孔。构造时，首先将原型图复制8份，通过PEG[15]算法获得一个32×24维度的基矩阵。然后在此基矩阵基础上结合文献[16]提出的圈长和外信息度量准则，将基矩阵每个单元扩充为128×128的排列阵或全零阵，从而得到最终的1/3码率的LDPC码，码长N=4096，M=3072，打孔点数为1024。从图3中可以看出，线性近似算法的误帧率曲线和BP算法曲线基本重合，对两者添加OSC处理后性能基本没有发生变化。而采用单一修正系数0.9的NMS算法虽然译码性能相距BP算法和线性拟合算法有一定的差距，但是在添加OSC处理后性能改进很明显，在 1 0-3的误帧率处，性能相对未加OSC处理的译码算法，提高了0.2 dB，相距BP算法也只有0.1 dB。

再按照图2中的ARJA原型图，构造1/4码率的LDPC码，并进行译码仿真，得到结果如图4。原型图构造类似前面AR4A的编码，首先复制9份，再用504×504的排列阵扩充，得到最终的LDPC码，码长N=4536，M=3528。该编码最大列重为12，同样部分变量节点需要打孔，打孔点数为504列，实际传输比特数为4032。图4中NMS算法采用单一系数0.7时译码性能较差，如果对3种不同行重(6,4,3)分布采用不同系数0.75，0.7，0.8，再结合OSC处理后，NMS算法的性能则得到大幅度改善，在 1 0-4误帧率处比单一系数的NMS性能改善0.2dB。而BP和线性拟合算法即便添加OSC处理，其性能改善有限。

图3 1/3码率AR4R原型图码字最大迭代次数为100时的误帧率曲线

图4 1/4码率ARJA原型图LDPC码在最大迭代次数为100时的误帧率曲线

6 结论

本文具体研究了基于原图构造的低码率 LDPC码的译码算法，通过在 NMS迭代译码算法过程中结合震荡抵消(OSC)处理和多系数(MF)修正技术，有效地改进了标准NMS算法译码性能。OSC处理和MF修正技术硬件实现简单，与标准的NMS算法相比，增加的译码复杂度和译码处理时延几乎可以忽略不计。通过仿真结果可以看出，对基于原图构造的一类低码率码字，OSC-MF-NMS译码算法性能更加逼近BP算法，性能改进显著。因此MFOSC-NMS算法是译码算法复杂度和性能之间一个较好的折中处理方案。

[1] Gallager R G. Low-density parity-check codes [J].IRE Transactions on Information Theory, 1962, 8(1): 21-28.

[2] Chung S Y. On the construction of some capacityapproaching coding schemes [D]. [Ph.D. dissertation], MIT,Cambridge, MA, 2000.

[3] Brink S ten. Convergence behavior of iteratively decoded parallel concatenated codes [J].IEEE Transactions on Communications, 2001, 49(10): 1727-1737.

[4] Qian D, Jiang M, and Zhao C,et al.. A modification to weighted bit-flipping decoding algorithm for LDPC codes based on reliability adjustment [C]. IEEE International Conference, Beijing, 2008: 1161-1165.

[5] Mobini N, Banihashemi A H, and Hemati S. A differential binary message-passing LDPC decoder [J].IEEE Transactions on Communications, 2009, 57(9): 2518-2523.

[6] Kim S, Jang M H, and No J S,et al.. Sequential messagepassing decoding of LDPC codes by partitioning check nodes[J].IEEE Transactions on Communications, 2008, 56(7):1025-1031.

[7] Chang Y M, Andres I, and Casado V. Lower-complexity layered belief-propagation decoding of LDPC codes [C]. IEEE International Conference, Beijing, 2008: 1155-1160.

[8] Chen J and Fossorier M P C. Near-optimum universal belief propagation based decoding of low-density parity check codes[J].IEEE Transactions on Communications, 2002, 50(3):406-414.

[9] Divsalar D, Dolinar S, and Jones C,et al.. Capacityapproaching protograph codes [J].IEEE Journal on Selected Areas in Communications, 2009, 27(6): 876-888.

[10] Gounai S and Ohtsuki T. Decoding algorithms based on oscillation for Low-Density Parity Check codes [J].IEICE Transactions on Fundamentals, 2005, E88-A(8): 2216-2226.

[11] Zhang J, Fossorier M, and Gu D. Two-dimensional correction for min-sum decoding of irregular LDPC codes [J].IEEE Communications Letters, 2006, 10(3): 180-182.

[12] Divsalar D, Dolinar S, and Jones C. Low-rate LDPC codes with simple protograph structure [C]. Proceedings International Symposium on Information Theory, Adelaide,2005: 1622-1626.

[13] Richter G, Schmidt G, and Bossert M,et al.. Optimization of a reduced-complexity decoding algorithm for LDPC codes by density evolution [C]. Proceedings 2005 IEEE International Conference on Communications, Seoul, Korea, 2005:642-646.

[14] Chen J, Dholakia A, and Eleftheriou E,et al.. Reducedcomplexity decoding of LDPC codes [J].IEEE Transactions on Communications, 2005, 53(8): 1288-1299.

[15] Hu X Y, Eleftheriou E, and Arnold D M. Regular and irregular progressive edge-growth Tanner graphs [J].IEEE Transactions on Information Theory, 2005, 51(1): 386-398.

[16] Tian T, Jones C, and Villasenor J D,et al.. Selective avoidance of cycles in irregular LDPC code construction [J].IEEE Transactions on Communications, 2004, 52(8):1242-1247.