基于粗数字高程模型信息的干涉相位图生成方法

郭 交 李真芳 刘艳阳 保 铮

(西安电子科技大学雷达信号处理国防科技重点实验室 西安 710071)

1 引言

干涉合成孔径雷达(InSAR)是获取地面数字高程图的重要遥感技术，它通过对同一地区获得的两幅SAR复图像的相位进行干涉处理，得到观测区域的3维地形图[1,2]。SAR图像配准和干涉相位滤波是InSAR数据处理中的两个关键步骤，图像配准精度和相位滤波性能直接影响后续的相位展开处理，最终影响DEM(Digital Elevation Model)的高程精度。因此，研究高精度的图像配准算法和稳健的相位滤波算法具有重要意义。

InSAR数据处理对SAR图像的配准精度要求很高，通常要求配准精度达到1/10-1/100个分辨单元[3,4]。然而，由于计算量巨大，传统的图像配准算法都是通过求取一定数量控制点的2维偏移量，采用多项式拟合的方法来获得SAR图像中每一像素的2维偏移量，从而完成整幅图像的精配准。在地形变化平缓和图幅比较小的情况下，传统的二次多项式已经能够满足精度，但是对于高程起伏剧烈的地形，或者对大幅图像进行处理时，通过二次多项式拟合求取偏移量必然会引入较大的误差，而采用更高次的多项式导致运算量增加和如何选取控制点等问题。

干涉相位滤波算法总是假定滤波窗口内的样本点满足独立同分布的假设，这样得到的滤波结果在统计意义上才等于滤波相位的均值，然而在InSAR数据的实际处理中，由于受地形起伏的影响，滤波窗口内的样本点不可能严格满足独立同分布，尤其在地形变化剧烈的地区，会导致滤波结果的偏离，最原始的圆周均值滤波方法，并没有对滤波窗口内的样本进行地形补偿，因此滤波性能欠佳。目前的地形补偿滤波算法都是假定在估计窗口内只有一个频率分量[5-7]，即滤波窗口内的样本点满足局部斜平面地形模型，通过参数估计的方法得到假定模型的参数，再对滤波窗口内的数据样本进行补偿。但是在实际处理中，假定局部平面模型存在一定的局限性，而且受地形起伏的影响，在每一个滤波窗口内都必须估计假定模型的参数，大大增加了运算量。

针对上述问题，本文充分利用已有的粗DEM图(例如，SRTM已经得到了全球80%的DEM)作为先验信息，提出了一种干涉相位图生成方法。在图像配准处理中，利用粗DEM信息和系统参数计算得到SAR图像中每一像素的2维配准偏移量，完成整幅SAR图像的配准。在干涉相位滤波中，利用已知的地形信息对SAR图像的地形相位进行统一补偿，再对剩余相位进行降噪滤波，可以提高相位滤波的性能，而且大大减小了运算量。另外，对于高分辨率SAR图像，由粗DEM的高程误差导致的图像配准精度可能还不满足InSAR处理的要求，因此本文提出再利用联合像素子空间投影的方法[8]进一步完成SAR图像精配准和相位滤波处理。

2 基于粗DEM信息的干涉相位图生成方法

本文提出了基于粗 DEM 信息的干涉相位图生成方法，充分利用已有的粗 DEM 数据来提高图像配准精度和相位滤波性能，同时降低运算量。此方法首先结合粗 DEM 数据和 InSAR系统参数，对SAR图像中的每一像素进行定位，然后求取相应像素的配准偏移量，进而完成整幅图像的配准。在相位滤波中，为使滤波窗口内的样本数尽量满足独立同分布，本文利用已知的粗 DEM 对干涉相位图中的地形信息进行统一补偿，显然，利用粗 DEM 数据对地形坡度进行统一补偿，然后再对剩余相位进行噪声抑制，可以大大减小运算量。

在低分辨率的情况下，例如SAR图像分辨率为3 m，利用粗DEM进行图像配准达到的配准精度已经足够高，能够满足 InSAR处理对配准精度的要求，因此对地形相位进行补偿后，采用传统的圆周均值滤波方法就可以对噪声进行有效抑制。然而，随着SAR系统的日益发展，SAR图像的分辨率不断提高，例如分辨率为1m，由粗DEM和系统参数误差导致的配准误差可能还不满足 InSAR处理的要求(假定InSAR处理要求的图像配准精度为1/20个像素)，基于粗DEM的图像配准只是相当于完成了粗配准，因此需要采用对配准误差具有强稳健的干涉相位估计方法，我们再采用联合像素子空间投影方法同时完成 SAR图像的精配准和干涉相位图的降噪滤波。由于已经对地形坡度进行了统一补偿，因此对滤波窗口内的样本不再需要任何补偿措施，同时还可以扩大样本的选取范围，从而获得满意的滤波结果。基于粗 DEM 信息的干涉相位图生成方法的处理流程如图1所示。

图1 基于粗DEM信息的干涉相位图生成方法处理流程

第1步 SAR图像像素定位 由于合成孔径雷达是采用2维平面对实际的3维空间进行成像，所产生的SAR图像是真实3维空间在雷达成像平面内的投影，存在信息的损失，因此直接对2维SAR图像的像素进行3维定位在原理上是不可行的。但是借助于已知的粗DEM信息，可以完成对SAR图像像素的粗定位，此定位精度取决于系统参数精度和粗DEM的高程精度。由于SAR图像与粗DEM的采样几何和坐标系定义不同(例如，通常情况下选择地固系为SAR成像坐标系，而DEM则为高斯-克吕格坐标系)，直接利用粗DEM数据是不可行的，需要在粗DEM中插值出SAR图像的每一像素。利用SAR图像和粗DEM信息对SAR图像像素进行定位的具体过程如下：由SAR图像以及轨道参数得到像素(i,j)的斜距R(i,j)和成像多普勒中心值fdc(通常选择成像多普勒中心为零赫兹，即fdc=0)；将像素(i,j)的高程值设定为参考高程值href(例如可以先对场景进行粗定位，结合粗DEM得到参考高程值)；用像素(i,j)的高程值对地球椭球方程进行修正，结合斜距方程和多普勒方程求取当前像素的坐标值，并将像素(i,j)的坐标值转换到高斯-克吕格坐标系下；在粗DEM中通过双线性插值得到当前像素对应位置的高程值hcur；计算参考高程和当前高程值hcur之差，即

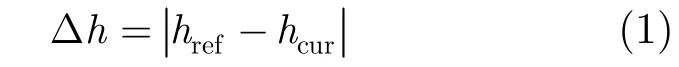
如果Δh小于门限值，则hcur就是像素(i,j)的高程值，此时，得到的像素(i,j)的坐标值就是当前像素的坐标值。否则更新参考高程值

再重新计算像素(i,j)的高程值。

对SAR图像中的所有像素依照上述步骤进行求解，就可以完成对整幅SAR图像中每一像素的定位。在对像素(i+1,j)或(i,j+1)进行定位时，我们设定其参考高程值为已经计算得到的像素(i,j)的高程值，来加快迭代运算的收敛速度。实际中，对于复杂地形，例如坡度较大的局部区域、山谷和陡峭山脉等，受雷达成像几何模型的限制，会产生高程层叠现象，此时对当前像素的定位可能会失败，因此在处理中当迭代次数大于门限值时，放弃对此像素的定位，而通过对其周围像素进行插值获得当前像素的位置估计。

文献[9]详细推导了各个误差源到SAR图像定位误差的传播公式，影响SAR图像像素定位精度的主要误差源为：卫星位置测量误差、卫星速度测量误差、斜距测量误差和高度误差。在本文方法中，高度误差取决于粗DEM高程误差和误差门限值Δh，其它为系统误差。

第2步 图像配准 完成了SAR图像像素定位之后，就可以由当前像素的斜距、成像多普勒中心、坐标值和系统参数计算得到当前像素在辅图像中的坐标值，然后根据计算得到的坐标值对辅图像进行插值重采样，从而完成SAR图像配准。

然而在实际中，由于存在系统误差和粗DEM高程误差，例如SRTM获得的全球DEM满足DTED-2标准[10,11]，必然会导致一定的配准误差，因此有必要对图像配准误差进行分析。

利用InSAR进行高程测量的几何模型如图2所示，其中X轴、Y轴和Z轴分别表示方位向、距离向和高度向，M和S为对地观测的主副天线，两副天线之间的距离B为基线长度，像素(i,j)的真实位置位于P点，由定位误差导致计算得到的像素位置为P′ 点，定位误差为(Δx, Δy, Δz)，R1和R2分别为主副天线到像素(i,j)的真实位置的斜距，为主副天线到像素(i,j)定位位置的斜距。根据图2中的几何关系可以计算得到点P在主辅图像中的距离偏移量Δr为

图2 InSAR进行高程测量的几何模型

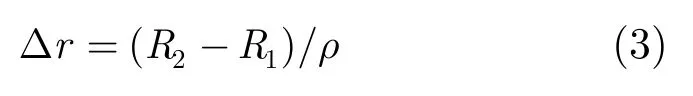
其中ρ为SAR图像的分辨率。若定位误差导致得到的像素位置为P′点，此时导致的图像配准误差Δrerr为

从以上分析可以看出，基于粗DEM的图像配准精度取决于SAR图像像素的定位精度和卫星位置误差。当卫星高度为600 km，卫星位置测量误差为1 m，卫星速度测量误差为0.05 m/s，斜距误差为3 m，DEM高程误差为30 m时，导致的SAR图像像素定位误差约为50 m。当垂直航向有效基线B⊥=1000 m时，根据式(3)和式(4)可以计算得到配准误差为0.08 m，当分辨率不高(例如3 m)时，能够达到的配准误差小于1/35个分辨单元，满足InSAR数据处理对配准误差的要求，但是在分辨率比较高的情况下，例如1 m，能够达到的配准误差约为1/12个分辨单元，当分辨率越高时，需要采取进一步措施提高图像配准精度。

第3步 地形坡度补偿 根据主辅图像的轨道参数以及SAR图像像素的坐标值，通过仿真生成已知粗DEM的地形干涉条纹图，利用此粗DEM地形相位对主图像中的地形相位统一进行补偿，去除已知的地形信息，形成新的干涉图像对。

第4步 干涉相位滤波 经过上述处理形成的InSAR图像对，已经完成了图像配准和地形相位补偿处理。当配准误差(第2步)小于1/20个SAR图像分辨单元时，图像配准已经达到了足够的精度，满足InSAR处理对图像配准的精度要求，此时可以采用传统滤波方法(例如圆周均值滤波方法)进行相位噪声抑制。然而当配准误差大于1/20个SAR图像分辨单元时，还需要对图像进行进一步精确配准再进行噪声抑制，针对这个问题，我们在文献[8]中提出了一种基于局部平面地形模型的联合像素子空间投影的方法，此方法对图像配准误差具有很强的稳健性，而且由于已经有效去除了InSAR干涉图像对中的已知地形信息，在滤波窗口内采用局域平面地形模型是合适的。

在干涉相位滤波完成以后，将补偿掉的地形相位再加入到干涉相位图中，最终生成滤波后的干涉相位图。也可以将干涉相位图和地形相位分别进行2维相位展开，将补偿掉的地形相位在解缠相位中进行补偿，生成解缠相位图。

3 算法性能仿真

本节利用仿真数据对本文方法进行性能仿真分析。

(1)基于粗DEM的图像配准法与传统配准方法的性能比较 我们先用仿真数据来验证基于 DEM进行图像配准的性能。仿真数据描述如下：假定两颗卫星进行编队飞行，垂直航向有效基线长度为813.5 m，卫星高度为600 km，下视角为45o，仿真地形如图3所示，最大高度为188 m，SAR图像的信噪比(SNR)为23 dB。相干系数由有效基线、局部地形坡度和信噪比决定。按照统计模型生成两颗卫星接收的SAR图像数据。SAR图像分辨率为3 m×3 m，粗DEM高程精度设定为30 m。

图3 仿真地形

图 4为对两幅 SAR图像进行配准处理后的结果：图4(a)和图4(b)分别为利用相关函数法进行粗配准和采用二次多项式拟合精配准后产生的干涉相位图，图 4(c)为基于粗DEM进行配准后产生的干涉相位图。图5为图像配准后的相干系数统计图。通过对仿真数据的处理结果可以看出，由于地形变化导致配准偏移量已经不满足二次多项式，而基于粗 DEM 的配准可以较精确地得到偏移量，能够提高图像配准精度。

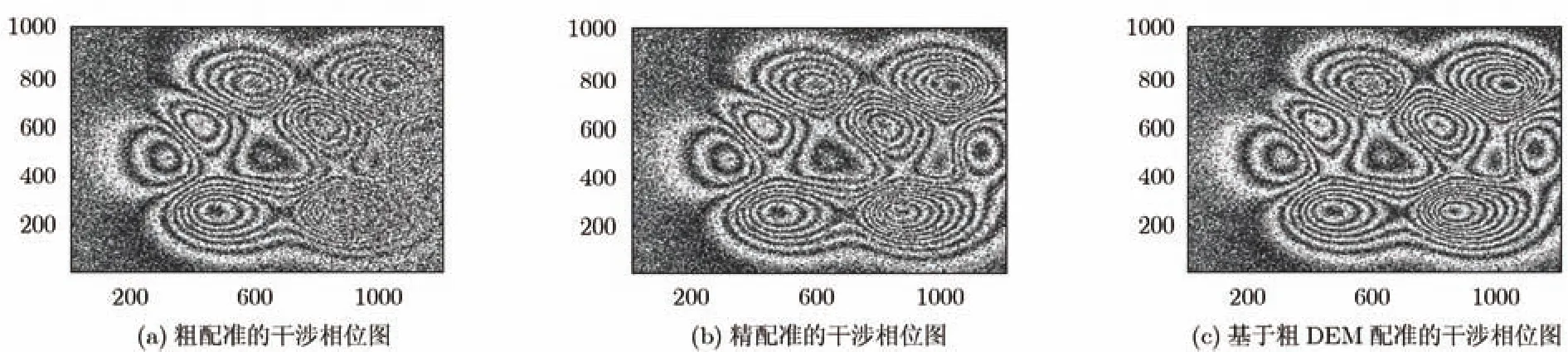
图4 配准处理结果

(2)基于粗DEM的相位滤波法与传统滤波方法的性能比较 下面利用仿真数据对本文方法的滤波性能进行分析。图6为干涉相位滤波结果：图6(a)为采用局部平面地形假设进行滤波的结果，图6(b)为基于局部斜平面地形模型的处理结果，图 6(c)为基于粗DEM地形模型进行滤波得到的干涉相位图。从图6中的仿真结果可以看出，基于斜平面模型和粗 DEM 对已知地形进行补偿后，使滤波窗口内的样本符合一致性假设，可以得到较理想的处理结果。然而，由于受地形变化的限制，基于局部斜平面模型必须逐个对滤波窗口内的样本进行参数估计，大大增加了运算量。而采用粗DEM对整幅SAR图像的地形进行统一补偿，可以大大提高算法的运行效率。

图5 相干系数统计图

图6 干涉相位滤波结果

(3)算法效率比较 基于粗DEM信息的干涉相位图生成方法相比于传统方法，增加了SAR图像像素定位处理，但大大减小了图像配准和相位滤波处理的运算量。因此，我们对上述的干涉图像(图像大小为1024×1200)对分别经过传统处理(相关函数法粗配准-相关函数法精配准-基于局部斜平面模型的干涉相位滤波)和本文方法处理(SAR 像素定位-图像配准-圆周均值滤波方法)，统计其运行效率，统计结果如表1所示。

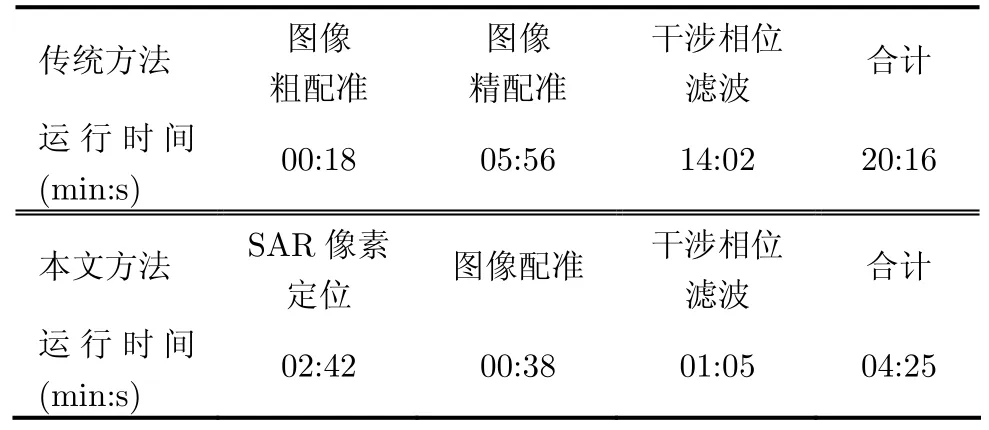
表1 运行效率对比

从表1对运算效率的统计结果可以看出：本文提出的基于粗 DEM 信息的干涉相位图生成方法有较高的运行效率，有利于大规模的数据处理。

4 结论

本文针对InSAR数据处理中的两大关键步骤：图像配准和干涉相位滤波，提出了一种基于粗DEM信息的干涉相位图生成方法，充分利用已有的粗DEM信息来改善SAR图像的配准精度和相位滤波性能，同时大大减小了运算量。

本文提出的干涉相位图生成方法首先利用粗DEM信息完成对SAR图像的定位，再根据系统参数完成SAR图像的配准和地形相位补偿。在SAR图像分辨率比较低时，利用粗 DEM 进行图像配准能够达到足够的配准精度，当分辨率比较高时，利用粗 DEM 进行图像配准达到的配准精度有可能不满足InSAR数据处理的要求，此时我们再利用联合像素子空间投影方法进一步完成图像精确配准和干涉相位滤波处理。由于对地形相位进行了有效地补偿，在相位滤波中采用局域平面地形模型更加合理。而且，随着雷达系统的发展和用户需求的提高，进行全球地形测绘的精度必然会越来越高，采用本文的方法也是一种逐步更新的思路，即结合之前得到的DEM和当前获取的InSAR数据来提高测绘地形的DEM精度。

[1] Rosen P A, Hensley S, and Joughin I R,et al..Synthetic aperture radar interferometry[J].Proceedings of IEEE,2000,88(3): 333-382.

[2] Peterson E H, Fotopoulos G, and Zee R E. A feasibility assessment for low-cost InSAR formation-flying microsatellites[J].IEEE Transactions on Geoscience Remote Sensing, 2009, 47(8): 2847-2858.

[3] 彭石宝，袁俊泉，向家彬. 一种基于加权迭代贪婪算法的InSAR相位解缠新方法[J]. 电子与信息学报, 2008, 30(6):1326-1330.Peng Shi-bao, Yuan Jun-quan, and Xiang Jia-bin. An improved InSAR phase unwrapping method based on interative-weighted greedy algorithm[J].Journalof Electronics&Information Technology, 2008, 30(6):1326-1330.

[4] Ferraluolo G, Meglio F, and Pascazio V,et al..DEM reconstruction accuracy in multichannel SAR interferometry[J].IEEE Transactions on Geoscience Remote Sensing, 2009, 47(1): 191-201.

[5] Meng D, Sethu V, and Ambikairajah E,et al..A novel technique for noise reduction in InSAR images[J].IEEE Geoscience and Remote Sensing Letters, 2007, 4(2): 226-230.

[6] Guarnieri A M and Tebaldini S. ML-based fringe-frequency estimation for InSAR[J].IEEE Geoscience and Remote Sensing Letters, 2010, 7(1): 136-140.

[7] Li Hai, Li Zhen-fang, and Liao Gui-sheng,et al..An estimation method for InSAR interferometric phase combined with image auto-coregistration[J].Science in China,Series F,2006, 49(3): 386-396.

[8] Li Zhen-fang, Bao Zheng, and Li Hai,et al..Image auto-coregistration and InSAR interferogram estimation using joint subspace projection[J].IEEE Transactions onGeoscience Remote Sensing,2006, 44(2): 288-297.

[9] Xu Hua-ping and Kang Chang-hui. Equivalence analysis of accuracy of geolocation models for spaceborne InSAR[J].IEEE Transactions on Geoscience Remote Sensing, 2010,48(1): 480-490.

[10] Krieger G, Moreira A, and Fiedler H. TanDEM-X: A satellite formation for high-resolution SAR interferometry[J].IEEE Transactions on Geoscience Remote Sensing,2007, 45(11):3317-3341.

[11] Gonzalez J H, Bachmann M, and Krieger G. Development of the TanDEM-X calibration concept: Analysis of systematic errors[J].IEEE Transactions on Geoscience Remote Sensing,2010, 48(2): 716-726.