低莱斯因子衰落信道下的Turbo码性能研究

张 婧

(桂林电子科技大学信息与通信学院，广西桂林541004)

0 引言

Turbo码［1］是一种具有良好译码性能的信道编码，由于其近Shannon界的突出纠错能力，已被采纳为3G和4G移动通信系统的信道编码标准之一。在Turbo码刚提出的最初几年，Turbo码的研究仅限于在AWGN信道［1］和Rayleigh信道［2］，而 Turbo 码在莱斯衰落信道下的研究相对较少［3，4］。文献［2］推导出了Turbo码在Rayleigh平坦衰落信道下的性能界和Turbo码BCJR译码算法在Rayleigh衰落信道下的修正。文献［3］分析了采用Viterbi译码算法时Turbo码在平坦Rician信道下的性能界。之后，Jinhong Yuan等人在［4］中给出Turbo码MAP译码算法和SOVA译码算法在Rician衰落信道下的修正算法，并指出MAP译码算法在平坦Rician衰落信道下的性能优于SOVA算法。但上述研究均未对Turbo码在低Rician衰落信道的性能进行研究。

文章首先建立了基于衰落信道的Turbo码系统模型，在此基础上对Turbo编译码器的设计及其相应算法进行讨论和研究，并用Matlab语言完成了Log-MAP及SOVA算法的仿真比较，最后对系统性能的仿真结果进行了分析。

1 系统模型

基于衰落信道的Turbo码系统模型如图1所示。其中，信道编码为Turbo码，采用BPSK调制。设信道是非频率选择性低Rician因子衰落信道，又受到零均值加性高斯白噪声干扰。通信速率较低，多径时延小于0.1T，因此可以不考虑码间干扰的影响，且多普勒频移为0 Hz，仅考虑多径传播引起的衰落对信号的影响。

图1 系统模型

该信道中，设在t时刻送入信道的信号为 xt，则接收信号［5］为

其中，at为信道衰落变化的随机变量，表示衰落幅度的包络;nt是加性白高斯噪声，其单边功率谱密度为 N0。衰落幅度的概率密度函数为

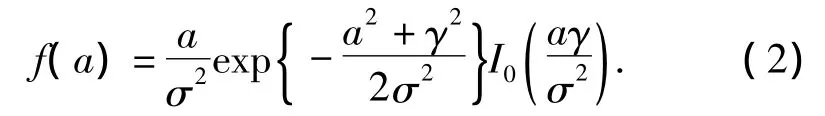
式中，I0(·)是零阶第一类修正贝塞尔函数。定义莱斯因子，即直视分量与随机散射分量之比。若K=0，信道为瑞利信道;若K=∞，则信道为高斯信道。

2 编码器结构及原理

一个常见的Turbo码编码器结构如图2所示。本文的编码器选用递归系统卷积码作为分量码，且两个分量码相同。交织器的使用伪随机交织器。伪随机交织器是由随机函数产生0－1的随机数，用排序函数求出其每个数据排序后对应的位置，最后输出置换位置的值。

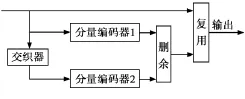
图2 Turbo码编码器结构

3 译码器结构及迭代译码算法

Turbo码获得优异性能的根本原因之一是采用了迭代译码，并通过分量译码器之间软信息的交换来提高译码性能。

3.1 Turbo码译码器结构

典型的Turbo码译码器是两个分量译码器经由一个交织器组成。其中分量译码器1和分量译码器2分别与Turbo码编码器中的两个分量编码器1和分量编码器2相对应，交织器和解交织器与编码器中的交织器和解交织器相对应。基本译码流程如图3所示。这里的外信息即为软信息。当经过数次迭代译码后，软信息就不再对Turbo码性能有影响，这时的输出经解交织和判决即可得到最终的译码输出序列。

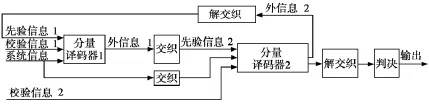
图3 Turbo码迭代译码流程

3.2 SISO迭代译码算法

为适应衰低Rician因子衰落信道，译码算法中的分支度量必须对条件概率p(yn|xn)进行修正。

3.2.1有信道状态信息的修正Log-MAP译码算法

Log-MAP译码中，t时刻输入符号的对数似然比Λ(ut)为

对于有理想信道状态信息的非相关Rician衰落信道，分支度量(yt，l′，l)可修正为

对数似然比Λ(ut)［1］可以分解成

其中，第一项是先验信息，第二项是系统信息，Λe(ct)是外信息，将Λe(ct)进行交织(或解交织)可以得到另一个译码器的先验信息。

3.2.2有信道状态信息的修正SOVA译码算法

SOVA译码算法需要计算出网格编码上的最大似然路径(ML)所对应的对数似然函数(LLR)，并将该对数似然函数作为SOVA算法的软输出。我们假设路径k在t时刻的状态序列为Sk，t，其路径度量为Mk(St)，可由下式递推计算

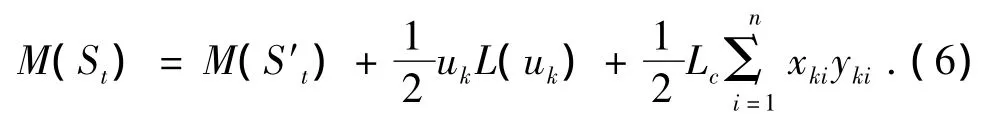
在Rician衰落信道中，对于完全交织信道且已知信道状态的情况下，(6)式应修正为下式

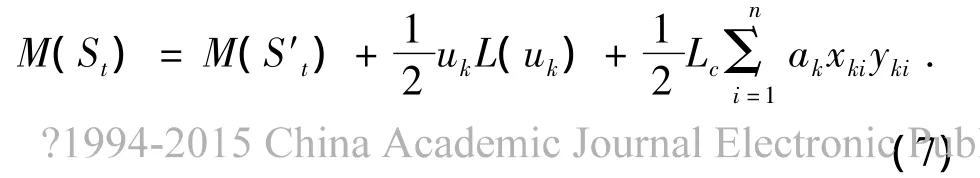
式中ak为信号幅度的乘性衰落因子。这样可以更精确地利用信道信息，使译码性能提高。

4 仿真结果与分析

本文分别对Turbo码Log-MAP算法和SOVA译码算法在低Rician因子衰落信道下的误比特率性能进行仿真。随机产生一组数据，使用两个相同的RSC分量编码器，生成矩阵为(1，13/15)8。将编码分别输入低莱斯因子单径衰落信道和多径衰落信道，且低Rician因子衰落信道的衰落因子分别为K= －5 dB，K=1 dB，K=3 dB，K=6 dB。帧长度为400 bit，完全交织。分别采用Log-MAP译码算法和SOVA译码算法。迭代次数设为5。图4为码率为1/2时，采用Log-MAP译码算法(a)和SOVA译码算法(b)在单径低莱斯因子信道中的系统性能。图5为码率为1/2时，采用Log-MAP译码算法(a)和SOVA译码算法(b)在多径低莱斯因子信道中的系统性能。

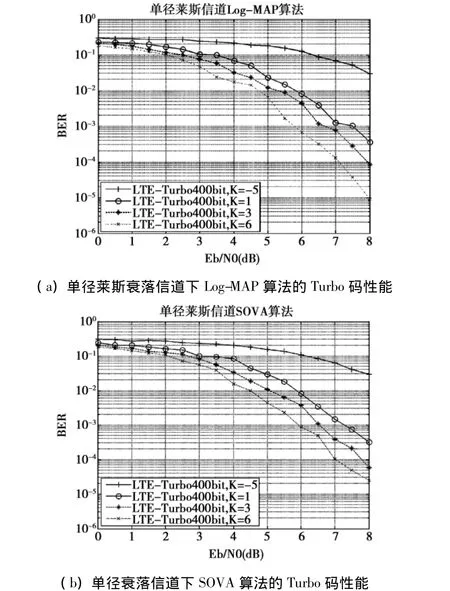
图4 码率为1/2，分别采用Log-MAP译码算法和SOVA算法，不同低莱斯因子信道下的Turbo码性能

图5 码率为1/2，分别采用Log-MAP译码算法和SOVA算法，不同低莱斯因子信道下的Turbo码性能

从仿真图可以得出几个结论:(1)不论单径衰落信道还是多径衰落信道，Turbo码在低Rician因子衰落信道下的误比特率随着莱斯因子的减小而衰落增大;(2)在单径低Rician因子衰落信道中，当误比特率为10－4时，采用Log-MAP译码算法比采用SOVA算法的性能好0.2～0.4 dB;(3)在多径莱斯信道中的Turbo码性能优于单径莱斯信道(在信噪比为8 dB时，Turbo码在多径莱斯信道的误比特率能达到10－5数量级，而在单径莱斯信道只能达到 10－4数量级)，说明，Turbo码具有抗多径衰落的性能;(4)不论单径衰落信道还是多径衰落信道，Turbo码的Log-MAP译码算法均优于SOVA译码算法，且在多径低莱斯因子衰落信道中，当BER为10－4时，Turbo码使用Log-MAP译码算法比使用SOVA算法的性能好0.5 dB。

5 结论

文章研究了适用于低Rician因子衰落信道的Turbo码译码算法，对Log-MAP译码算法和SOVA译码算法在低Rician因子信道下作了修正，并对这两种算法进行Matlab仿真。仿真结果表明，在信噪比较低的情况下，使用Turbo码在低Rician因子衰落信道中能达到较好的性能，且在多径低莱斯因子信道中，Turbo码能获得优于单径莱斯衰落的性能。

［1］Berrou C，Glavieux A，Thitimajshima P.Near Shannon Error-correcting Coding and Decoding:Turbocodes［A］.ICC 1993，Geneva，Switzerland，1993.1064 －1070.

［2］Eric K，Hall，Stephen G.Wilson.Design and Analysis of Turbo Codes on Rayleigh Fading Channels［C］.IEEE Journal on Selected Areas in Communications，1998，16(2):160－174.

［3］Fulvio Babich，Guido Montorsi，Francesca Vatta.Improved Union Bounds on Turbo Codes Performance in the Rician Fading Channel［A］.IEEE VTS 50th Vehicular Technology Conference［C］.United State:IEEE，Piscataway，NJ，1999:2178 －2182.

［4］Jinhong Yuan，Branka Vucetic.Turbo Code Performance on Rician Fading Channels* ［A］.ICC’99.IEEE International Communications Conference［C］.United States:IEEE，Piscataway，NJ，June，1999:83 －87.

［5］周万胜，万燕，朱洪波.Rice衰落信道的统计特性分析与仿真［J］.南京邮电学院学报，2000，20(2):27 －31.

［6］刘继承，姚建红，邵定蓉，等.Rician衰落信道下Turbo码性能分析［J］.遥测遥控，2004，25(1):1 －5.

［7］Valenti，Matthew C，Woerner.Brian D.Performance of Turbo Codes in Interleaved Flat Fading Channels with Estimated Channel State Information［A］.IEEE Vehicular Technology Conference［C］.United States:IEEE，Piscataway，NJ，1998.