信息时标不一致对传递对准的影响及修正
解春明,赵 剡,杨传春
(1. 北京航空航天大学 仪器科学与光电工程学院,北京 100191;2. 桂林空军学院,桂林 541003;3. 防空兵指挥学院,郑州 451002)
空空导弹发射前,弹载捷联惯导系统需要利用高精度主惯导信息进行传递对准,对准精度直接影响导弹子惯导系统的导航精度,进而决定导弹的命中精度。但是,主子惯导信息时标不一致普遍存在于传递对准过程中,导致滤波估计产生很大误差。本质上,信息时标不一致的产生有两个主要原因:①子惯导仅在导弹发射前某一时刻开机并快速完成传递对准,其启动的随机性以及与主惯导信息输出频率的不同造成了信息时标的不一致;②传递对准中,主惯导的导航参数通过串行数据总线传递给机载火控系统,机载火控系统处理完这些信息后,再通过串行数据总线传递给导弹惯导系统,测量反应、数据处理、信息传输、接收对准信息的延迟时间都会造成匹配信息的时标不一致[1]。前一个因素产生的时标偏差通常可以通过递推得出,且相对固定;后一个因素产生的时标偏差则与惯导系统、机载火控系统、传输总线性能相关,存在很大的随机性。整体看来,主子惯导信息时标不一致导致了主子惯导输出不同步、对准匹配周期随机、参考匹配信息滞后。
针对此问题,国内外许多学者进行了研究。文献[2-5]研究了舰载导弹和机载导弹传递对准中主子惯导信息不匹配的问题,将延迟时间作为随机常值扩充为系统状态进行估计。考虑到实际对准匹配周期的随机性,时间延迟不满足随机常值的假设,因此文献[2-5]的方法难于适用。文献[6]采用不等间隔滤波方法进行组合导航,解决了周期不固定的滤波问题,但该方法先利用带时标误差的匹配量进行滤波,再进行信息滞后的修正,导致滤波估计波动较大,且该方法计算时间长,存储信息多,不适合针对小量估计的高精度快速传递对准的实施。
本文从原理上分析了信息时标不一致对机载传递对准产生的影响,提出利用子惯导的硬件中断获取主子惯导时标差,先采用内插量测匹配实施等周期滞后滤波,再利用外推法对随机时标差进行补偿,全面解决了信息时标不一致问题造成的信息不匹配和对准匹配周期随机对传递对准造成的影响。
1 信息时标不一致对传递对准的影响分析
在主子惯导信息时标不一致的情况下进行传递对准,其量测量可以表示为:

通常,传递对准采用易于实施的水平面机动,如“S”型机动、变速直线机动等,能够实现较好的对准效果。
1)当载机通过协调转弯实现“S”型机动时
本文以东北天地理系作为导航坐标系,速度为:

式中,V0为载机的轨迹速度,机动过程中保持恒定;ψ为航向角。对式(6)两边求导,得到:

2)当载机采用匀变速直线运动时
取载机水平朝北机动,速度公式为:

依据式(10)可概略计算“S”型机动中由时标差引起的量测误差大小可达0.4 m/s左右;依据式(12)可计算变加速直线飞行中时标差引起的北向速度量测误差大小可达0.5 m/s,而此时的理论差约为1.6 m/s,其影响不可忽视。实际对准中,待估失准角越小,时标差的影响越显著。
2 信息时标不一致的修正
2.1 传递对准状态空间模型
1)状态方程
为了简化问题的研究,将机翼的弹性变形以注入噪声的方式加以等效,考虑传递对准滤波模型由速度误差、失准角、陀螺的随机常值漂移和加速度计的随机常值偏置组成,建立系统状态方程为[8];


式中,δVE、δVN、δVU为速度误差,VE、VN、VU为速度分量,ieω为地球自转角速率,R为地球半径,iε为陀螺随机常值漂移,i▽为加速度计随机常值偏置,其余符号规定同第一部分。
2) 量测方程
采用“速度”匹配方案进行主、子惯导量测匹配,其中主惯导参考匹配量在滤波中利用惯性器件输出和杆臂矢量进行补偿。量测方程为:

2.2 时标不一致的修正方法
1)内插法进行量测匹配
对准中,为了避免修正时标差带来的显著影响,需要对主子惯导进行时标统一,通常可采用外推法和内插法。通过文中第一部分结论可知,在时标相差时间段内速度的一阶导数V˙(t)与多个参数有关,其规律十分复杂。如果对主惯导速度进行外推与子惯导速度匹配,不但外推公式难以确定,而且Δt有可能比主惯导速度解算周期大很多,所以外推值会存在很大的误差,造成进入滤波器的匹配量可信度降低。而采用内插法确定子惯导在主惯导时标处的信息,则匹配的精确度会大大提高。其优势在于内插所用数据都是子惯导已经计算获取的数据(子惯导解算时保存),而且插值点必落在子惯导速度解算的一个周期内。
标减去时标差得到的插值点的子惯导数据。拟合公式为:

实际中,可根据机动的复杂程度增减拟合阶数n。

式中,Tf=N·TMINS为主惯导速度解算周期的整数倍(固定值);Δtk、 Δtk-1为相邻两个匹配点的主、子惯导时标差(随机值)。
显然,Tzk是个随机值,所以量测匹配和滤波变成了变周期过程。变周期滤波中,需要频繁处理系统方程和观测方程的离散化问题,容易造成滤波发散。而通过内插法进行时间回溯的量测匹配时,子惯导信息正好滞后Δtk,如式(24),使得任意两次量测周期固定为Tf。因此,可以在每次子惯导收到主惯导信息的时标处进行等周期(Tf)滞后滤波。
这样,由于内插法可获得高精度量测数据,只需采用传统卡尔曼滤波便能够保证滞后时刻滤波结果的精度,且存储信息量小,运算速度快。对状态方程和量测方程进行离散化处理,离散化周期为Tf。离散卡尔曼滤波方程为:
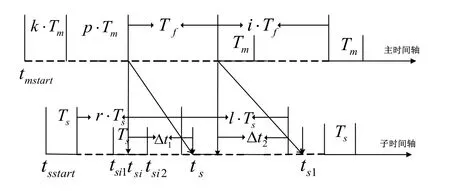
图1 主子惯导信息传递Fig.1 Information transmission between MINS and SINS

3)随机时标差的补偿
由于采用等周期滞后滤波,造成滤波估计滞后,需要补偿随机时标差的影响,将滞后的估计信息修正到子惯导的当前时标处。一种思路是,在每次等周期滤波后,在时标差Δtk时间段内重新对系统方程和量测方程以Δtk为周期进行离散化处理,然后进行时间更新得到子惯导当前时刻的状态估计值和估计方差Pk,时间更新公式为:
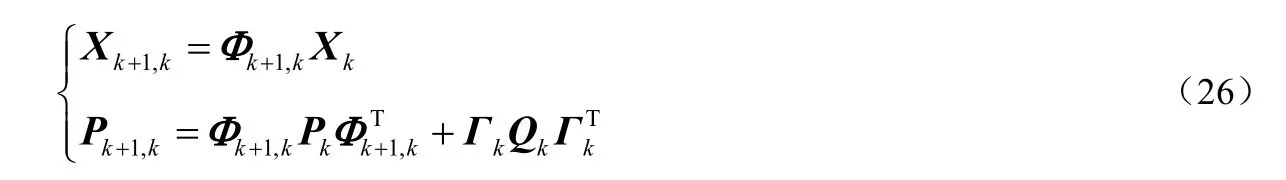
采用这种思路,必须保存时间更新前的等周期滤波结果以维持后续滤波,且需要额外进行矩阵运算。这里采用另外一种思路:仅存储过去时间一定数量的滤波状态估计值,利用前述的多项式拟合法推算子惯导当前时刻的滤波值。推算值用以显示输出,不参加卡尔曼滤波迭代过程。考虑到内插匹配的等周期滞后滤波的估计结果精度较高,这里采用一阶拟合算法以减小计算量,公式为:

3 仿真及结果分析
3.1 仿真条件
初始位置为经度116°,纬度40°,高度5000 m,初始速度300 m/s,初始姿态角为0;假设主惯导无误差,子惯导陀螺常值漂移0.1(°)/h,加速度计零偏为100μg;各向安装误差角均取1°;状态初始值设为0,初始方差P0,系统噪声Q和量测噪声R由陀螺和加速度计的误差确定。仿真时间20s,滤波周期0.5s,子惯导启动时刻为2.35s,主惯导速度解算周期0.01 s子惯导速度解算周期0.02 s,时标差为40~120 ms之间的随机数。飞行轨迹设置为:①“S”型机动为4段5 s横滚运动,横滚角度为20°、-20°、-20°、20°;②“S”型机动为4段5s横滚运动,横滚角度为40°、-40°、-40°、40°;③变加速直线机动为4段5 s北向变加速直线运动,加速度为5 m/s、-5 m/s、5 m/s、-5 m/s。④变加速直线机动为4段5 s北向变加速直线运动,加速度为10 m/s、-10 m/s、10 m/s、-10 m/s。
3.2 仿真结果
仿真结果如图2~图5所示,其中,虚线和实线分别表示未进行时标差修正和进行时标差修正的失准角估计误差曲线。图2、图3表示进行不同强度“S”型机动时失准角的估计误差结果,图4、图5表示进行不同强度变速直线运动时失准角估计误差结果。
3.3 仿真结果分析
由图2虚线部分结果可以看出,未进行时标差补偿时,在机动强度较小的“S”型机动中,时标差主要影响东向速度量测,产生较大的横滚角估计误差。图3虚线部分显示当“S”型机动强度增加时,不仅东向速度量测偏差继续增大,北向速度量测偏差也开始明显,三个失准角的估计效果都有所下降。

图2 采用轨迹①机动时失准角估计误差图Fig 2 Misalignment estimation errors of maneuver①
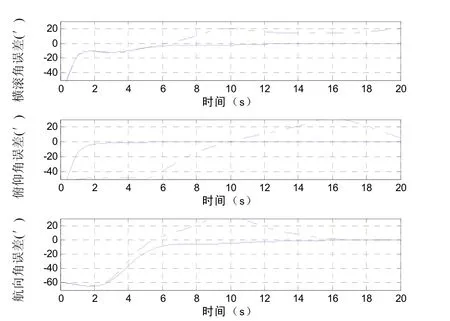
图3 采用轨迹②机动时失准角估计误差图 Fig 3 Misalignment estimation errors of maneuver②
图4、图5虚线部分表示未进行时标差补偿时,不同变速直线运动强度下对准滤波估计结果,由于主要是北向速度量测产生偏差,因此俯仰角的估计产生误差,误差大小随机动强度而增强。可以看出,滤波受时标差影响的偏差趋势和量级与文中第一部分分析结论一致。虚线结果还表明,时标差导致滤波估计偏差的同时也降低了滤波收敛速度。各图中实线部分为经过时标差补偿的结果,其中时标差的影响被大幅抑制,对准收敛速度和精度都得到了保证;而且,采用本文修正方法进行滤波,估计曲线比文献[6]中方法平稳。

图4 采用轨迹③机动时失准角估计误差图Fig 4 Misalignment estimation errors of maneuver③

图5 采用轨迹④机动时失准角估计误差图Fig 5 Misalignment estimation errors of maneuver④
4 结束语
针对传递对准中普遍存在的信息时标不一致问题,从原理上推导出它与对准机动的初始参数、机动强度和持续时间等参数的关系,分析了它对传递对准滤波的影响及修正的必要性,进而提出问题的修正方法。该方法先利用过去数据进行内插匹配,接着实施等周期滞后滤波,最后利用高精度滤波估计值进行外推时标差补偿。在对不等周期滤波问题的解决中,此方法存储信息少、滤波平稳、精度高。仿真结果不仅验证了时标不一致对传递对准影响的原理分析结论,而且表明了修正方法对该影响的有效抑制能力,保证了高精度快速传递对准滤波的收敛速度和精度,具有重要的工程价值。
[1] 鲁浩,位晓峰. 空空导弹捷联惯导系统总体设计与仿真研究[J]. 电光与控制,2007,14(2):128-132.LU Hao, WEI Xiao-feng. Simulation research and overall design for SINS of air-to-air missile[J]. Electronics Optics &Control, 2007, 14(2): 128-132.
[2] You-Chol L, Joon L. Transfer alignment error compensator design using H∞filter[C] //Proceedings of the American Control Conference, 2002: 1460-1465.
[3] Joon L, You-Chol L. Transfer alignment error compensator design based on robust state estimation[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2005, 48(61): 143-151.
[4] 扈光锋,王艳东,范跃祖. 传递对准中测量延迟的补偿方法[J]. 中国惯性技术学报,2005,13(1):10-14.HU Guang-feng, WANG Yan-dong, FAN Yue-zu. Compensation method for measurement delay in transfer alignment[J].Journal of Chinese Inertial Technology, 2005, 13(1): 10-14.
[5] Joon L, You-Chol L. Transfer alignment considering measurement time delay and ship body flexure[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 195-203.
[6] 刘建业,熊智,段方. 考虑量测滞后的INS/SAR组合导航非等间隔滤波算法研究[J].宇航学报,2004,25(6):626-631.LIU Jian-ye, XIONG Zhi, DUAN Fang. Processing the measurement delay INS/SAR integrated navigation in-coordinate interval filtering algorithm study[J]. Journal of Astronautics, 2004, 25(6): 626-631.
[7] 魏志刚. 空空导弹系统信息延迟时间的测试分析[J]. 航空兵器,2005(5):7-9.WEI Zhi-gang. Test and analysis of information transmit delay in air-to-air missile system[J]. Aero Weaponry, 2005(5): 7-9.
[8] Wei Gao, Yue Yang-ben. Performance comparison of two filtering approaches for INS rapid transfer alignment[C] //International conference on mechanics and automation, 2007: 1956-1961.

