环形激光陀螺人工神经网络温度漂移建模

杨鹏翔，秦永元, 游金川

（西北工业大学 自动化学院，西安 7100072）

环形激光陀螺仪(RLG)是现代高精度捷联惯性导航系统设计时通常被采用的惯性传感器件，由于RLG结构设计中的热设计缺陷和内部机械抖动部件的温度不稳定性等原因[1]，导致其输出脉冲信号中通常含有一定的零偏漂移误差(下文简称漂移)。文献[2]通过改进惯性器件的热设计来进行补偿；文献[3]则通过设计温度补偿系统来减小测量误差；文献[4-5]利用温箱对RLG进行高、低温和变温循环测试，并基于实验建立了漂移随温度、温度变化率等多因素相关的误差模型，并取得了较好的补偿效果。

常规的RLG单表温度试验条件过于理想，当工作环境下存在温度迅速改变（温度冲击）时，内部温度场并不均匀，与实际工作环境不符，只适合出厂前的性能测试与摸底。考虑到RLG在实际应用时，系统箱体外部通常满足“三防”要求，其隔离和保护作用保证上电以后，系统内部温度上升均匀、缓慢。因此，本文从这一角度出发，将系统在常温下上电，工作过程中通过温箱设置不同的系统外部环境温度，利用系统工作过程中的内部温升获得温度漂移测试数据。几组不同热环境下长时间静态测试结果表明，RLG漂移与温度（单因素）之间的关系具有很好的重复性。仅考虑温度值的影响时，温度和漂移之间关系为高阶非线性模型。提出了采用人工神经网络技术[5-6]对该漂移模型进行辨识。对实测数据进行小波降噪以压缩训练样本，然后分别采用人工神经网络中较为成熟的BP和RBF网络和低阶分段最小二乘（LS）技术对少量测试样本进行学习，将经过训练建立起来的RLG漂移模型应用到新测得的四组数据中进行有效性检验，证明了人工神经网络温度漂移建模方法的有效性。若采用均方误差(MSE)指标进行评价，该方法可使RLG的稳定性指标提高20%-40%，且采用BP网络建模优于一阶分段线性拟合，RBF网络建模优于二阶非线性分段拟合。

1 环形激光陀螺漂移

SINS通常由IMU本体（惯性器件+内框架）、电子线路和箱体外壳组成，壳体的设计一般满足气密性要求。IMU本体与壳体内壁通过若干橡胶减震垫隔离开来。这种结构一方面使得RLG工作过程中产生的热量难以通过壳体向外传导，影响了系统的散热；另一方面，壳体与IMU本体之间充填的气体和橡胶等热不良导体也隔离或减弱了外部环境温度变化（或温度冲击）对RLG内部温度场的影响，使得陀螺的漂移表现为受系统壳体内部温度场的温度值影响最为明显。

进行如下温度漂移测试实验：选用温箱外置的三轴速率位置转台进行试验，转台和压缩机通过隔振基座分离，以避免空气压缩机振动对测试结果带来影响。通过标定工装将SINS的x-y-z陀螺敏感轴调整至地理系东-北-天方向，并使转台往南倾斜，倾斜角L等于当地纬度，常温下（25℃）彻底冷却后，按照如下三种测试条件展开试验：

条件1：常温上电，保温（精度±1℃），直至系统内部温度升至60℃，停止测试，冷却；

条件2：常温上电，温升速率1℃/min，目标温度30℃，保温，直至系统内部温度升至60℃，停止测试，冷却；

条件3：常温上电，温升速率1℃/min，目标温度50℃，保温，直至系统内部温度升至60℃，停止测试，冷却。

扣除各位置输出脉冲的常值部分后，剩余量视为陀螺温度漂移量。本文在多个位置重复进行了以上实验，获得了较好的重复性。图1给出了其中同一位置时，上述三种不同温度环境下的x陀螺漂移百均值化曲线，由于在60℃高温附近有个别陀螺出现工作不稳定噪声突变等，故下文仅截取25～55℃温度范围内的数据进行建模。

由图1可知，该陀螺温度漂移曲线幅度最大时可达0.06 (°)/h，三组漂移曲线和温度的对应变化趋势具有很好的重复性，温度拐点基本一致。基于以上实验，本文认为RLG在系统内工作时，由于壳体具有的隔离和保护功能，内部温度场变化缓慢、均匀，对外部环境温度影响不敏感，而主要表现为对温度场中温度值的敏感，在这种情况下的温度漂移建模只需考虑温度单因素的影响，又因为曲线变化趋势较为复杂，难以通过低阶模型准确拟合漂移曲线的，下文研究通过人工神经网络技术进行漂移曲线的模型拟合。

图1 不同环境温度条件下RLG漂移曲线Fig.1 RLG drifts under different temperature circumstance

2 人工神经网络

人工神经网络（ANN）是人工智能领域的一种处理非线性问题的常用方法，广泛应用于函数逼近、模式识别/分类、数据压缩等领域[6-7]。在人工智能领域，基于前馈反向传播网络BP神经网络模型和基于径向基函数的RBF神经网络模型应用最为成熟，神经元是神经网络的基本组成单元，典型的BP和RBF神经元结构分别如图2和图3所描述。

图2和图3中，PR表示输入向量元素，wi,j表示输入向量的第R个输入元素与输入层的第i个神经元之间的连接权值，b表示神经元的激活阈值，n表示传输函数f的输入量，a为神经元输出。

用向量形式将BP神经元简洁地描述为如下数学形式

由此可知，BP神经元和一般的神经元结构是类似的，表示的是神经元输入向量的加权和如果大于阈值θ=-b，则激活神经元，由传输函数f产生输出aBP，常用的非线性f函数是S型传输函数，如对数(logsig)和双曲正切函数(tansig)等，但这两种非线性函数的值域会导致该类神经元输出值会限制在(0, 1)之间，而当采用线性传输函数(purelin)则可以输出任意值。相比之下，RBF神经元的传输函数f为径向基函数，且一般采用高斯函数，其向量形式可描述为如下数学形式：

图2 BP神经元Fig.2 Structure of BP neuron

图3 RBF神经元 Fig.3 Structure of RBF neuron

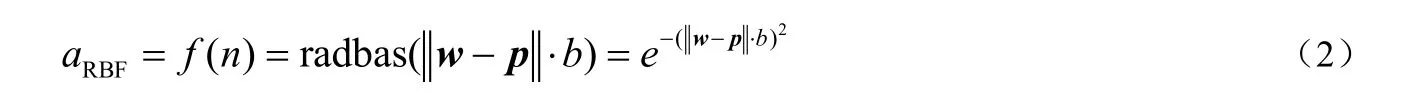
3 实验及分析

由于只对陀螺进行温度单因素影响建模，为减小网络训练的复杂度，可为三个轴向的RLG分别设计单输入单输出网络。尽管许多文献给出了网络结构设计时对网络层数和神经元个数选取的经验公式，但在很多情况下，这些经验公式并不凑效[7]，本文经过多次试探，确定一个四层结构的BP神经网络对25～55 ℃范围内RLG测试数据训练，可以达到较好效果。该BP网络具有三个隐层，各隐层皆具有10个神经元，输出层为1个神经元，四层网络的传输函数依次为三个双曲正切函数(tansig)和一个线性函数(purelin)，误差性能函数选择为均方误差性能函数（MSE），网络层的权值函数为附加动量因子的梯度下降权值/阈值学习函数(learngdm)，以减小BP网络训练时陷入局部极小的概率，拟牛顿反向传播(BFGS算法)训练函数则被用于训练该网络。RBF网络的层数为传统的2层结构，第一层为隐层，其RBF神经元个数通过网络创建函数(newrbe)在训练过程中自动确定，输出层为一个线性函数(purelin)。

利用在常温环境下的长时间静态测试所得温度和漂移测试数据作为网络的训练所用的学习样本，该测试数据中以10秒间隔采样获得，共计4096组数据，如直接输入至网络供其训练，会带来相当的计算强度。为了提高训练速度，并减小测试噪声对网络训练所造成的误差，按照如下措施对学习样本进行预处理：首先利用Matlab中的排序函数(sort)将对应温度的漂移原始数据按照温度值升序重新排序；然后，利用小波降噪方法[7]对测试数据进行软阈值降噪预处理，得到光滑的温度和漂移测试曲线；最终，从降噪后的测试样本中等间隔地抽取256个点作为学习样本进行训练，分别采用BP和RBF网络建立了如图4和图5中所示的神经网络拟合曲线模型。

图4 BP神经网络模型拟合曲线Fig.4Curve modeled by BP neural network

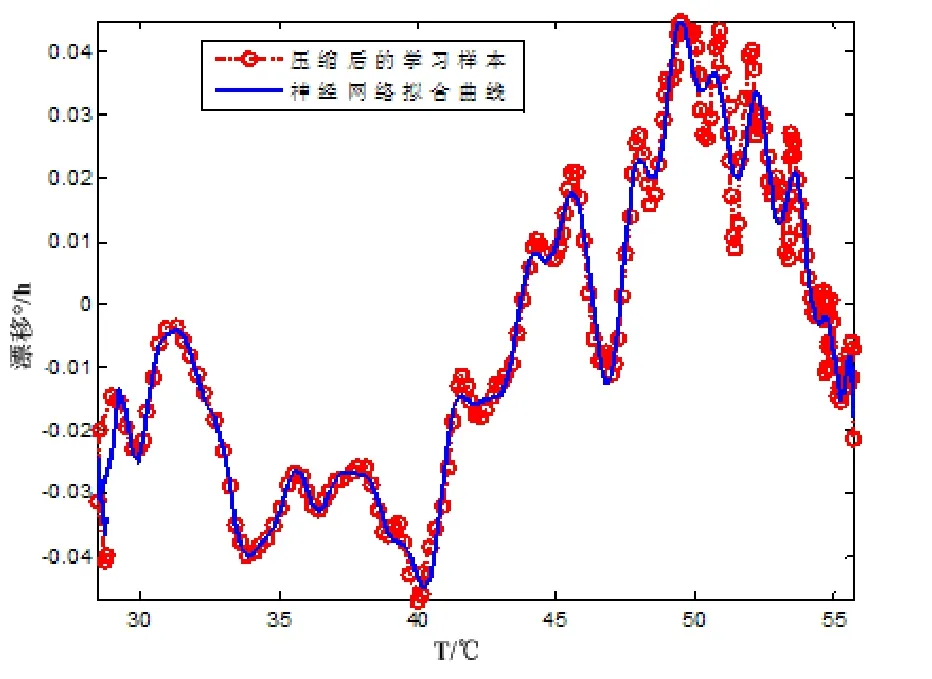
图5 RBF神经网络模型拟合曲线 Fig.5 Curve modeled by RBF neural network

为了对比检验人工神经网络温度漂移模型效果，同时利用最小二乘分段拟合中的一阶线性模型和二阶抛物线模型对样本进行处理，获得的曲线在图6和图7中给出。

图6 一阶线性分段拟合模型Fig.6 First-order piecewise fitting with linear model

图7 二阶抛物线分段拟合模型Fig.7 Second-order piecewise fitting with parabola

利用上述建立起来神经网络模型和低阶最小二乘分段拟合模型分别对四组新测得的检验样本进行补偿，得到补偿前后的均方根误差（RMS）强度如表1所示。

表1 陀螺温度不同补偿模型及其误差(RMS)Tab.1 Different modeling method and fitting error result (RMS)

由表1中的统计结果可见，补偿前的RLG稳定性约为0.025 (°)/h，在采用以上所提多种方法对RLG的零偏随温度漂移的高阶非线性模型进行拟合，稳定性可以小于0.02 (°)/h，可提高稳定性指标为20%～40%，且综合来看，BP神经网络的补偿效果要优于一阶线性分段补偿，RBF网络优于二阶抛物线分段补偿。

4 结 论

本文基于SINS不同外部环境温度下的静态漂移测试实验，确认RLG漂移与SINS内部温度场的温度单因素关系最为显著，在忽略温度变化率和温度梯度前提下，利用BP和RBF神经网络对25～55 ℃范围内漂移进行温度建模，随后利用新测的四组样本对所建立起来的模型进行有效性检验，结果证明可将RLG的稳定性指标提高20%～40%。与常规低阶分段最小二乘拟合方法相比，BP网络建模精度要优于一阶线性分段补偿，RBF网络优于二阶抛物线分段补偿。此外，由于全反射棱镜加工工艺[9]或一些其他的缺陷，实验所采用的RLG在低温环境下工作时存在不稳定现象，解决这一问题尚需时日，故没有进行低温条件下的温度补偿试验；且由于本文所提补偿方法仅能减小或削弱RLG与内部温度场有关的漂移趋势项，其常值部分的补偿仍然需要通过系统级标定[10]或工艺改进来实现，这是下一步需要深入研究的问题。

[1] 金世龙，龙兴武，王飞，等. 激光陀螺克服高、低温冲击的技术研究[J]. 光学学报，2006，26(3)：409-414.JIN Shi-long, LONG Xing-wu, WANG Fei, et al. Technology research for ring laser gyro to overcome the environmental temperature variation[J]. Acta Opticasinica, 2006, 26(3): 409-414.

[2] Fidric B G. Ring laser gyro frame design resistant to thermal gradient effects[P]. US: 4867567. Sep.19, 1989.

[3] Buchler R J, Moellert L R, Fann S W, et al. Temperature compensation method for strapdown inertial navigation system[P].US: 6175807, Jan.16, 2001.

[4] 高玉凯，邓正隆. 机抖温度特性对激光陀螺零偏稳定性的影响[J]. 中国惯性技术学报，2007，15(3)：351-354.GAO Yu-kai, DENG Zheng-long. Dithering mechanism temperature’s influence on bias stability[J]. Journal of Chinese Inertial Technology, 2007, 15 (3): 351-354.

[5] 张鹏飞，龙兴武. 机抖激光陀螺捷联系统中惯性器件的温度补偿的研究[J]. 宇航学报，2006，7(3)：522-526.ZHANG Peng-fei, LONG Xing-wu. Research on temperature compensation model of inertial sensor in mechanically dithered RLG’s SINS[J]. Journal of Astronautic, 2006, 7(3): 522-526.

[6] Y M Shao, Z Zhao, L Wang, H O He. Drift data modeling of laser gyro based on neural networks[C]// Conference of the 2006 International Symposium on Instrumentation Science and Technology, 2006, Vol.48: 128-133.

[7] Kai-Wei Chiang. INS/GPS integration using neural networks for land vehicular navigation applications[D]. Alberta: Doctoral Dissertation of University of Calgary, 2004, 11: 126-34.

[8] Moody J, Darken C J. Fast learning in networks of locally-tuned processing units[J]. Neural Computation, 1989(1): 281-294.

[9] Bakin Y V, Ziouzev G N, Lioudomirski M B. Laser gyros with total reflection prisms[R]. AGARDograph AGARD AG, 1999,Chapert 6: 1-29.

[10] 周琪，秦永元，严恭敏，等. 激光捷联惯性组件精确标定技术研究[J]. 测控技术，2008，29(9)：95-98.ZHOU Qi, QIN Yong-yuan, YAN Gong-min, et al. Precision calibration techniques research for laser strapdown inertial measurement unit[J]. Measurement & Control Technology, 2008, 27(9): 95-98.