用低精度双轴转台对捷联惯导进行系统级标定的方法

周章华，邱宏波，李 延，练 涛，王 婷

（北京自动化控制设备研究所，北京 100074）

捷联惯导系统测量单元主要由加速度计和陀螺仪组成，其中陀螺仪目前主要有激光陀螺仪和光纤陀螺仪等。由于制造工艺等因素影响，捷联惯导系统的主要误差源是惯性器件误差，而惯性器件误差又分为随机误差和确定性误差两部分，其中确定性误差是系统误差的主要部分，因此在使用前必须通过标定试验确定系统各项误差系数，并在捷联惯导系统中进行补偿[1-2]。

传统的标定方法包括静态多位置试验方法和角速率试验方法两种[3-5]。其中静态多位置试验方法的基本原理是利用转台提供的方位基准和水平基准，将地球自转角速度和重力加速度作为输入捷联惯导系统的标称量，并与系统中陀螺仪和加速度计的输出进行比较，根据陀螺仪和加速度计的误差模型，建立捷联惯导系统的误差模型，然后将精密转台转动到多个不同位置，当位置数与误差模型中的未知数即误差系数的个数相等时，即可通过联立的方程组求解出各项误差系数。而角速率标定是利用转台给捷联惯导系统输入一系列标称的角速度，并与捷联惯导的输出比较，根据捷联惯导系统的误差模型，即可确定出捷联惯导角速度通道的标度因数和安装误差两类误差系数。上述两种标定方法的不足之处在于对转台的精度要求较高，系统的标定精度依赖转台精度和惯导系统在转台上的安装精度，是一种分立标定方法。

为降低捷联惯导系统标定对转台精度的要求，捷联惯导系统级标定技术是目前主要研究方向。系统级标定的关键是建立导航输出误差与惯性器件误差系数之间的关系，充分考虑惯性器件误差系数的可辨识性，合理安排实验位置，进而辨识出惯性器件的各项误差系数。文献[6][7]均研究了基于三轴转台翻滚的一种标定模型及具体的标定实验设计，但未进行激光捷联惯组误差参数的完全辨识设计；而文献[8]从理论上分析了惯性仪表误差系数的可辨识性和位置编排原则，给出能够标定出捷联惯导24个误差系数的辨识方法。本文在上述研究的基础上，模型中考虑加速度计二次非线性项误差系数，具体提出了一种基于低精度双轴转台的捷联惯导系统十位置系统级标定方法，并通过试验验证了该方法可全面准确的标定出系统各项误差系数。

1 惯性组件误差模型

捷联惯导系统的惯性组件通常包括相互正交安装的三个陀螺和相互正交的三个加速度计（定义为Ax、Ay、Az）。在对捷联惯导系统进行标定前，需要选定惯组坐标系XYZ，其定义为：坐标系XYZ与捷联惯导固联，X与Ax加速度计的敏感轴重合，Y轴位于由Ax和Ay加速度计敏感轴组成的平面中，Z轴与X、Y构成正交坐标系。

考虑加速度计标度因数的非线性影响，加速度计组合的误差模型可写为[9]：

2 基于低精度双轴转台的SINS系统级标定方法

2.1 双轴转台位置编排

图1 双轴转台10位置标定位置编排Fig.1 Ten-position arrangement on two-axis turntable

考虑高精度三轴转台使用成本，结合试验室现有资源，本文提出利用低精度双轴转台对捷联惯导系统进行系统级标定。利用静态时姿态误差在±1°内的双轴转台，将捷联惯导系统安装在双轴转台上，起始位置XYZ指向北天东，启动惯导系统；在第一个位置静置2 min后，转台按图1中所示方向转动到第二个位置；静置2 min后再转到第三个位置，按图1中位置编排依次进行；到第十个位置静置2 min后即可关闭系统，利用保存的加速度计和陀螺仪脉冲数据对系统24个误差系数进行标定。

2.2 系统误差系数与导航误差结果关系建立

首先利用加速度计和陀螺仪数据对惯导系统进行对准，对准完成后从第1个位置开始进入导航，对导航的速度误差δVn和航向误差δψ进行测量并记录，作为导航误差观测量。根据系统速度误差和姿态方程：

2.3 系统误差系数确定

3 试验验证

为了验证该10位置系统标定方法的可行性和准确性，本文从数学仿真试验和实物试验两方面进行验证。

3.1 数学仿真试验

在给定的标定参数的基础上，通过数学仿真产生10位置标定过程的加速度计和陀螺脉冲数据，然后利用10位置标定程序处理该数据，标定出的系统误差系数与给定系统误差系数如表1所示，可以看出，10位置标定方法全面准确地标定出了系统误差系数。

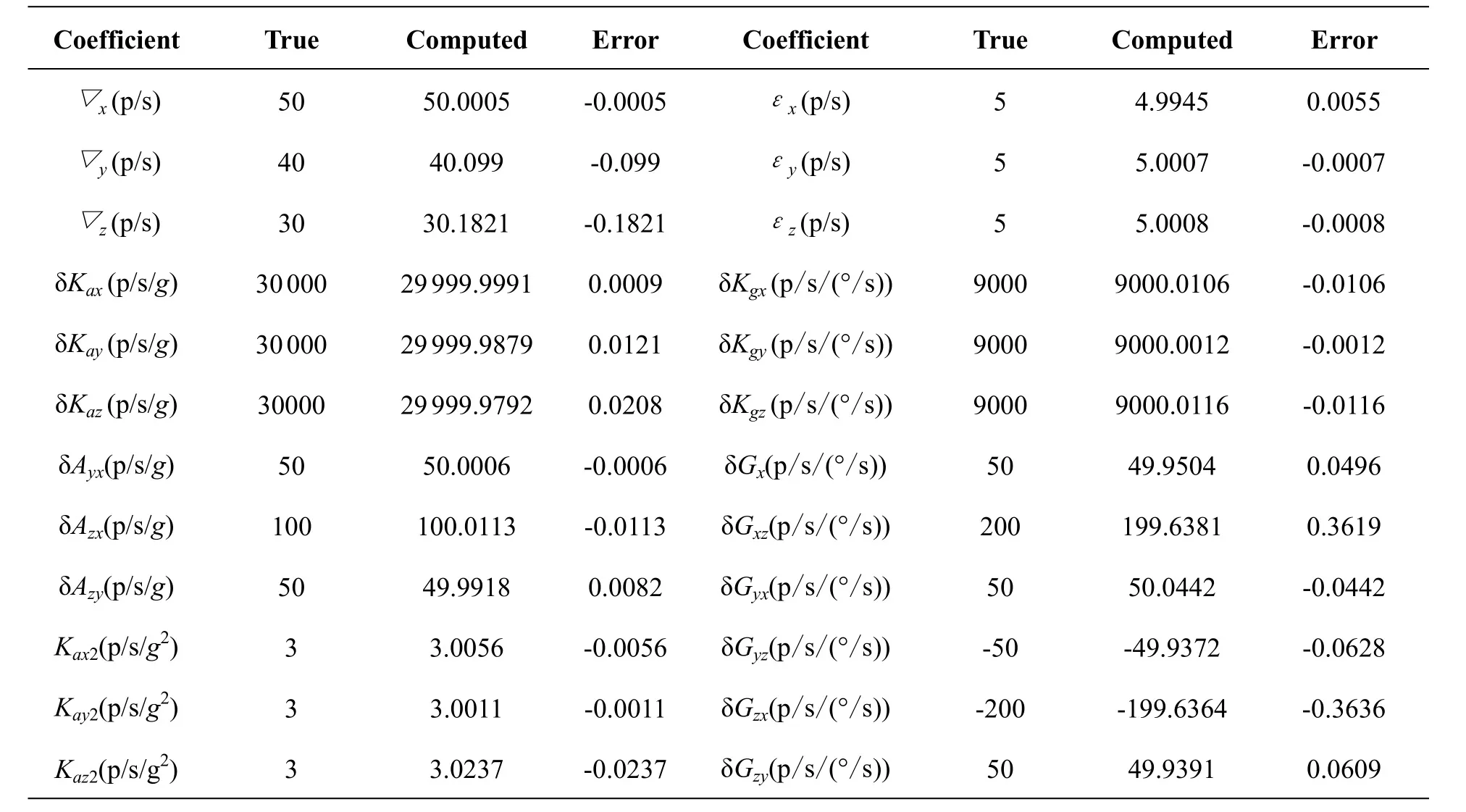
表1 系统误差系数给定值与标定结果比较Tab.1 Comparison of calibration result of the true and computed error parameter

3.2 实物试验

试验采用某型激光捷联惯导系统，惯性器件由三个激光陀螺仪和三个石英挠性加速度计等组成。首先将惯导系统在高精度三轴转台上利用传统方法进行标定。然后将系统安装在某型双轴转台上，控制转台转动使其到指定位置有一定角度（±1°）偏差，采用本文中提出的10位置系统级标定方法进行标定，试验结果如表2所示。

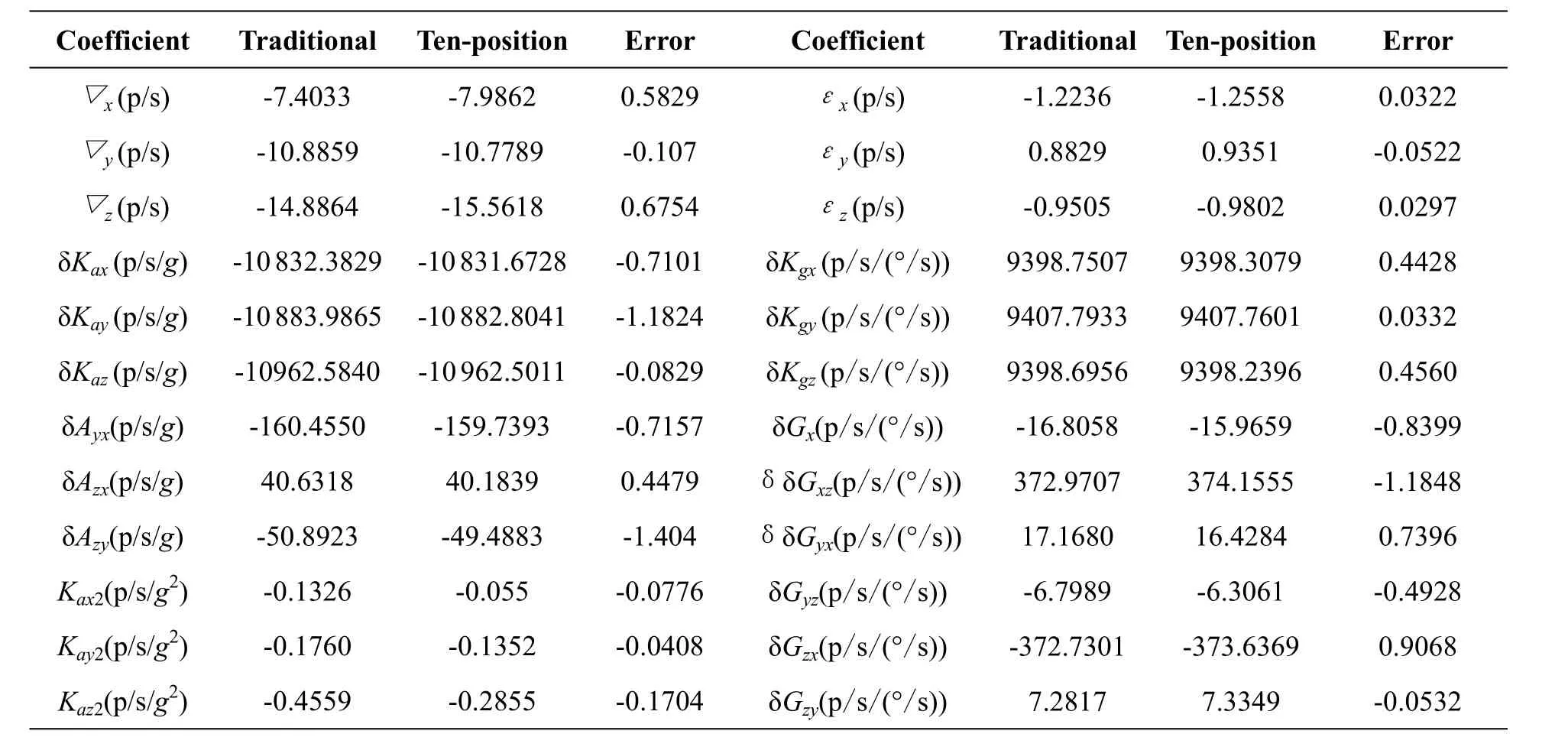
表2 十位置标定方法与传统标定方法试验结果比较Tab.2 Comparison of test result of ten-position and traditional calibration method

从表2中可以看出，利用10位置标定方法对捷联惯导系统在低精度双轴转台上进行标定，其结果与在高精度三轴转台上利用传统方法进行标定的结果精度相当，其中加速度计零偏最大相差6 μg，加速度计标度因数最大相差95 ppm，加速度计安装误差最大相差26″，陀螺仪零偏最大相差0.015(º)/h，陀螺仪标度因数最大相差42ppm，陀螺仪安装误差最大相差26″。

4 结 论

本文从工程需要的角度出发，提出了一种利用低精度双轴转台对捷联惯导系统进行 10位置系统级标定的方法，该方法通过合理的位置编排，在连续翻转过程中使系统各项误差系数激发导航误差，利用导航速度和方位误差作为导航误差观测量，从而全面辨识出捷联惯导的包括加速度计标度因数非线性系数在内的24个系统误差系数。通过实际系统进行标定发现，系统在低精度双轴转台上的10位置标定精度同在精密转台上利用传统方法标定精度相比，标度因数最大差值不大于100ppm，安装误差最大差值不大于30″。该标定方法标定精度不依赖系统在转台上的安装精度，降低了标定成本，且标定位置少，标定时间短，辨识参数精度较高，对中低精度捷联惯导系统具有较高的工程应用价值。

（Reference）：

[1] Pei-hwa Lo, Donald Siebert, Herbert T Califano. Low Cost Fiber Optic Rate Sensor Inertial Measurement Unit [C]// Position Location and Navigation Symposium. Palm Springs, CA, USA: IEEE, 1998: 256-263.

[2] Curey R K, Ash M E, Thielman L O, et al. Proposed IEEE inertial systems terminology standard and other inertial sensor standards[C]// Position Location and Navigation Symposium. Montery, CA: IEEE, 2004: 83-90.

[3] Eduardo Nebot, Hugh Durrant Whyte. Initial calibration and alignment of low-cost inertial navigation units for land vehicle applications [J]. Journal of Robotic Systems, 1999, 16(2): 81-92.

[4] LIU Qin, LIU Li, QI Zai-kang. Error analysis and compensation of strapdown inertial navigation system [J]. Journal of Beijing Institute of Technology (English Edition), 2002, 11(2): 117-120.

[5] Yun Cho Seong, Gook Park Chan. A calibration technique for a redundant IMU containing low-grade inertial sensors [J]. ETRI Journal，2005, 27(4): 418-425.

[6] 张亮. 激光陀螺捷联惯导系统的系统级标定方法研究[D]. 北京：中国运载火箭技术研究院，2007：35-42.ZHANG-Liang. Research on the systematic calibration method for laser gyro SINS [D]. Beijing: China Academy of Launch Vehicle Technology, 2007: 30-42.

[7] 郭美凤，滕云鹤，章燕申. 激光陀螺惯性导航系统静态校准方法研究[J]. 中国惯性技术学报，1997，5(4)：24-27.GUO Mei-feng, TENG Yun-he, ZHANG Yan-shen. Research on the static calibration method for a laser inertial navigation system[J]. Journal of Chinese Inertial Technology, 1997, 5 (4): 24-27.

[8] 杨晓霞，黄一. 激光捷联惯导系统的一种系统级标定方法[J]. 中国惯性技术学报，2008，16(1)：1-7.YANG Xiao-xia, HUANG Yi. Systematic calibration method for laser gyro SINS[J]. Journal of Chinese Inertial Technology,2008，16(1): 1-7.

[9] 邱宏波，周章华，李延. 光纤捷联惯导系统高阶误差模型的建立与分析[J]. 中国惯性技术学报，2008，15(5)：530-535.QIU Hong-bo, ZHOU Zhang-hua, LI Yan. Establishment and analysis on high-order error model of FOG SINS[J]. Journal of Chinese Inertial Technology, 2008, 15(5): 530-535.