一类拟线性时标动力方程的Lyapunov型不等式

张启明，周 欣

（湖南工业大学 理学院，湖南 株洲 412007）

1 研究背景

经典的Lyapunov不等式是指在特定的边值条件下，Hill型方程有非平凡解时需满足的必要条件。该不等式最初由俄国数学力学家李亚普列夫[1]，于1907年在考虑常微分方程的解的稳定性时提出。即有如下引理1。

引理1[1]设q(t)是[a,b]上实值连续函数，若Hill型方程

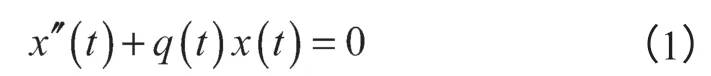
存在非平凡实解x(t)，且满足边值条件

则有

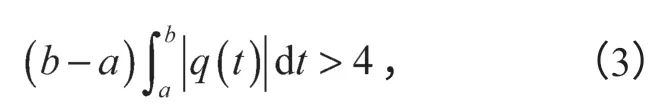
其中不等式（3）右边的下界“4”不能被更大的常数代替。

人们称不等式（3）为经典的Lyapunov不等式。此后，不等式（3）被推广到许多的方程和系统中，这些改进或推广后所得的Lyapunov不等式即为Lyapunov型不等式。

20世纪80年代，德国学者S.Hilger最先在其博士论文[2]中提出了时标的概念，并建立了一些基本的时标理论。此后，时标理论在文献[2-4]的基础上得到蓬勃发展。其中，B.Kaymakcalan在1996年出版的著作[5]中，建立了时标上动力方程的Lyapunov稳定性理论。M.Bohner和A.Peterson在文献[6-7]中，系统分析了时标上一类非常重要的动力方程：时标上的动力方程。时标上的动力方程（系统）不仅可以包括连续和离散这两种特殊的情形，而且在应用上也蕴含巨大的潜力，是一个比较新的有着广泛应用前景的应用数学分支，其理论研究主要集中在边值问题、振动性、稳定性、不共扼性等方面[8-12]。本文将在预备知识部分对时标的基本概念和基本理论作简要介绍。

关于时标上的动力方程（系统）的Lyapunov型不等式，文献[11-19]中分别对时标上的Hill型方程、Hamilton系统、一阶非线性系统以及拟线性系统进行了研究，得到了许多重要的结果。其中文献[11-12]是通过建立Lyapunov型不等式来讨论其稳定性的。

本文考虑下述拟线性时标动力方程

并建立一些新的Lyapunov型不等式。

特别地，当β1=α2=0，α1=p=β2=q=γ，r1(t)=r2(t)=r(t)，f1(t)=f2(t)=Q(t)时，方程（4）退化为二阶半线性时标动力方程

式中：γ＞1，r(t)＞0。

2 预备知识

时标是指实数集R上任意的非空闭子集，通常记作T。

定义1[7]设T为时标，对任意t∈T，当σ(t):=inf{s∈T:s＞t}时，称σ:T→T为前跳跃算子；当ρ(t):=sup{s∈T:s＜t}时，称ρ:T→T为后跳跃算子。

对函数f:T→R，下面给出函数f在点t∈Tk时的Δ（或Hilger）导数的定义。

定义2[7]设t∈Tk，函数f:T→R，若对任意ε＞0，存在t的邻域U，使得对任意s∈U都有

则称fΔ(t)为f在t的Δ（或Hilger）导数。

引理2[7]设函数f,g:T→R在t∈Tk都可微，则：

i）对任意常数a,b，af+bg:T→R在t也可微，且(af+bg)Δ(t)=afΔ(t)+bgΔ(t)；

ii）若fΔ(t)存在，则f在t连续；

iii）若fΔ(t)存在，则；

iv）fg:T→R在t可微，且

v）若g(t)g(σ(t))≠0，则f/g在t可微，且

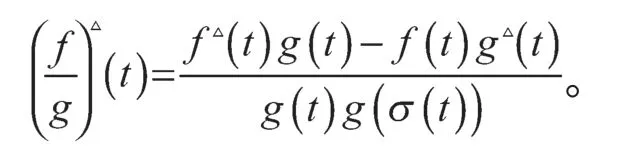
定义3[7]函数f:T→R称为rd连续的，若它在T中的右稠密点连续，在T中的左稠密点的左极限存在且有限，记作Crd=Crd(T)=Crd(T,R)。

定义4[7]对任意t∈Tk，若FΔ(t)=f(t)，则称函数F:T→R为f:T→R的原函数，并记Cauchy积分为

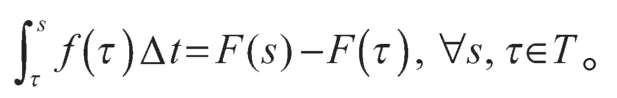
引理 3[7]若a,b,c∈T，k∈R，且f,g∈Crd，则：

vi）对t∈[a,b)，若|f(t)|≤g(t)，则。

引理 4[7]（Cauchy-Schwarz不等式） 设a,b∈T，1＜p，q＜+∞，且满足1/p+1/q=1，则对函数f,g∈Crd，有不等式成立。

3 主要结果及证明

首先，给出如下假设：

H1 对任意t∈T，r1(t),r2(t),f1(t),f2(t)∈Crd，并且r1(t)＞0，r2(t)＞0。

H2 对i=1,2，系数p,q,αi,βi满足αi/p+βi/q=1，且1＜p,q＜+∞，αi＞0,βi＞0，并记

定理1设a,b∈Tk,σ(a)≤b，且假设H1和H2成立，如果方程（4）的非平凡解(u(t),v(t))满足边值条件

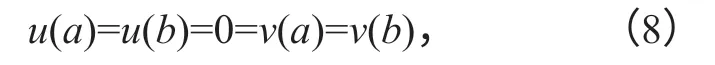
其中u(t)不恒等于0，对任意t∈[a,b]，则

证明利用时标积分和边值条件（8），可将方程（4）化为式（10）和式（11）：

由式（6）（8）以及Cauchy积分的定义和引理4，可得式（12）和式（13）：

由式（12）和式（13），可得

从而，由式（8）（10）（11）（14）以及假设H2和引理4，可得

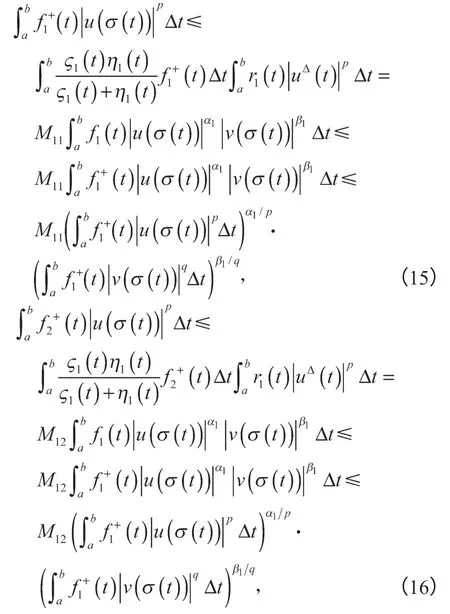
其中

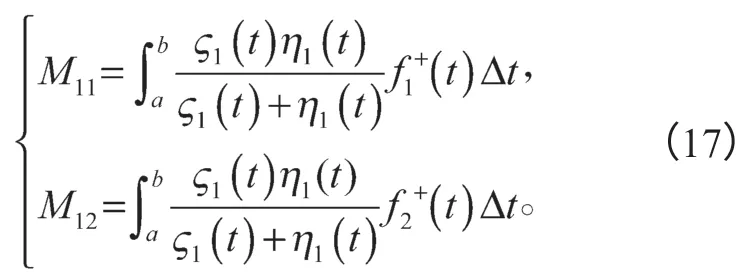
类似地，由式（7）（8）和引理4，有

从而，由式（8）（10）（11）（18）以及假设H2和引理4，可得

其中

下证

事实上，若命题（22）非真，则有

从而由假设H2以及式（10）（23）可得

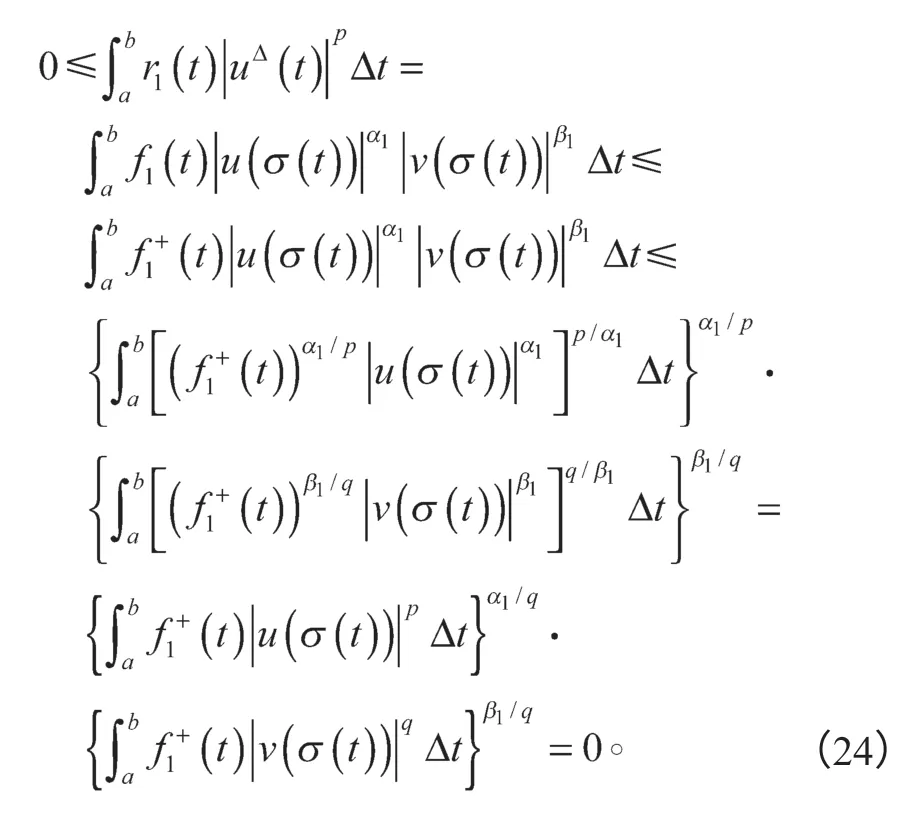
根据式（24）和假设H1有

从而对一切a≤t≤b，由式（12）（25）可得u(t)≡0。这与边值条件（8）矛盾，所以不等式（22）成立。

类似地可证下述不等式

成立。进而由式（15）（16）（19）（20）（22）（26）以及假设H2可得

再结合式（17）（21）即可得结论（9）成立。

推论1设a,b∈Tk，σ(a)≤b，且假设H1和H2成立，如果方程（4）的非平凡解(u(t),v(t))满足边值条件（8），则

证明由(i=1,2)、式（9）及假设H2可直接证得式（28）成立。

推论2设a,b∈Tk，σ(a)≤b，且假设H1和H2成立，如果方程（4）的非平凡解(u(t),v(t))满足边值条件（8），则

证明由

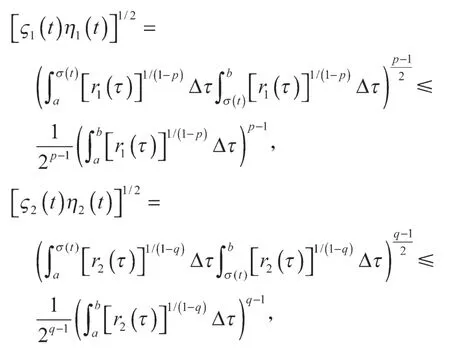
以及式（28）和假设H2可直接证得式（29）成立。

对二阶半线性动力方程（5），由式（14）或（18）易得下述定理2。

定理2设a,b∈Tk，σ(a)≤b，如果方程（5）有一个非平凡解u(t)满足边值条件

其中u(t)不恒等于零，对任意t∈[a,b]，则

由于

由定理2可直接得下述推论3。

推论3设a,b∈Tk，σ(a)≤b，如果方程（5）有一个非平凡解u(t)满足边值条件（30），则

4 结语

本文在边值条件（8）下，建立了拟线性时标动力方程（4）的Lyapunov型不等式；进而探讨了作为时标动力方程（4）的特殊情形的二阶半线性时标动力方程（5），在边值条件（30）下的Lyapunov型不等式。所得结果可为进一步研究时标动力方程解的特性提供参考。