算术结构拉普拉斯矩阵最大特征值的上界

，，

（湖南师范大学 数学系，湖南 长沙 410081）

1 研究背景

对于一个连通图G，如果向量，则称为G的算术结构；如果条件

A(G)=(aij)，i～j表示i与j相邻；d、r都为列向量，所有的元素都是正整数，rT为向量r的转置矩阵。

给定一个简单图G，其拉普拉斯矩阵为

图的算术结构的概念，是Lorenzini研究代数几何中退化曲线时，出现交矩阵而引入的[1]。近年来，关于算术结构的研究较多，如文献[2]研究了完全图、路和圈上算术结构的一些性质；文献[3]研究了路和圈上算术结构的个数等。代数图论是图论的一大分支，它利用图的关联矩阵的代数性质来研究图。特别地，图谱理论主要研究它的邻接矩阵、拉普拉斯矩阵的特征值和图的性质之间的联系[4]。

2 预备知识

为了证明本文将给出的有关结论，先介绍一些相关的知识和结论。

定义矩阵

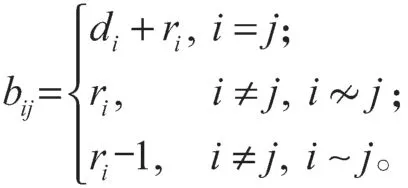
因为L(G,d)是实对称矩阵，它的特征值为实数，故可设为。

引理1[5]设A是一个n阶任意矩阵，其特征值为λ1≥λ2≥…≥λn，为对应于特征值λk的特征向量，q为任意n维的列向量，则矩阵A+vqT的特征值为

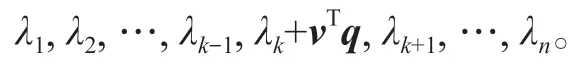
定理1设G是一个n阶连通图，则B(G)的特征值为

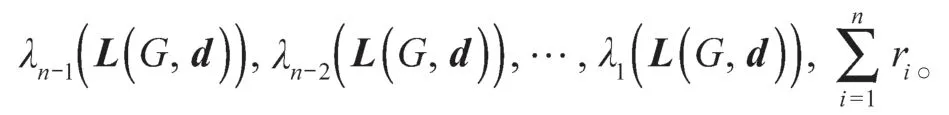
证明由B(G)=L(G,d)+re可得，B(G)r=L(G,d)r+rer。

因向量r中每个元素都是正整数，G连通，矩阵B(G)非负不可约，所以由Perron-Frobenius定理知，er是B(G)的谱半径，且r是其Perron向量，即

由引理1可以得到B(G)的特征值为

推论1设G是一个n阶连通图，(d,r)为G上的一个算术结构，则

3 算术结构的拉普拉斯矩阵特征值更精确的上界

引理2[8]设M(G)=(mij)是一个n阶非负实对称矩阵，若有一个对应于谱半径的正特征向量，为M(G)的第二大特征值，则有

定理2设G是一个n阶连通图，为G上的一个算术结构，则

证明由知，，从而r是对应的正特征向量。

设

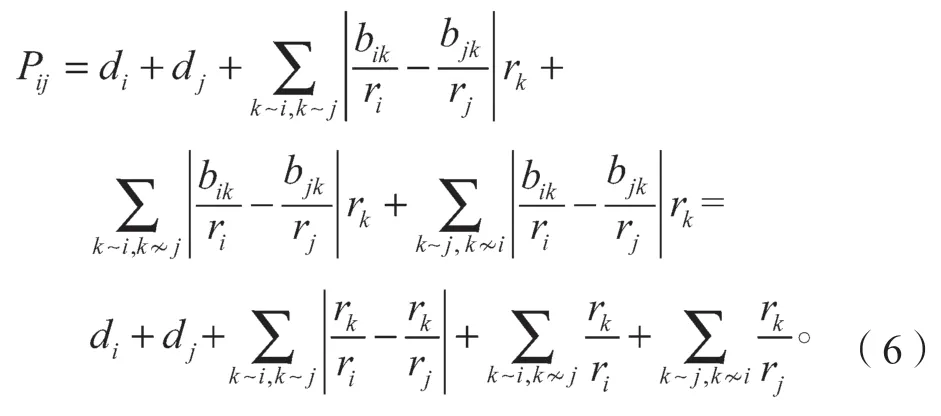
当i～j时，则

由式（6）和式（7）可得，

由引理2可知，

定理3设G是一个n阶连通图，(d,r)为G上的一个算术结构，则

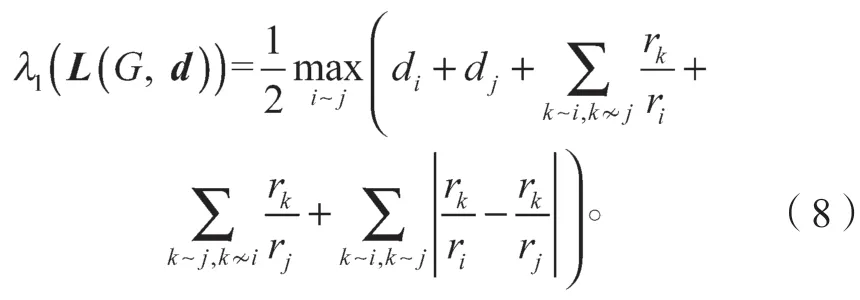
证明令R=diag(r1,r2,…,rn)，定义矩阵，则C(G)的元素为

因为矩阵C(G)与L(G,d)相似，所以它们有相同的特征值，令x是矩阵C(G)对应于特征值的特征向量。

由上述2个等式可得

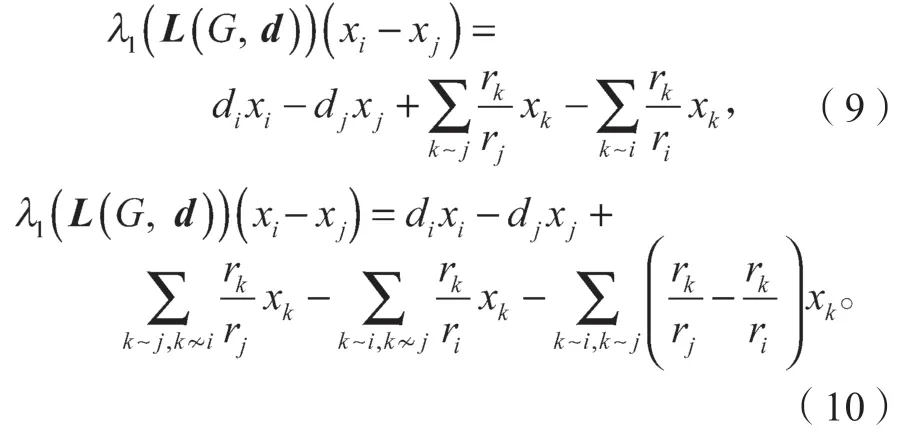
因为xj≤xk，xk≤xi，所以由式（10）得

设

其中

所以

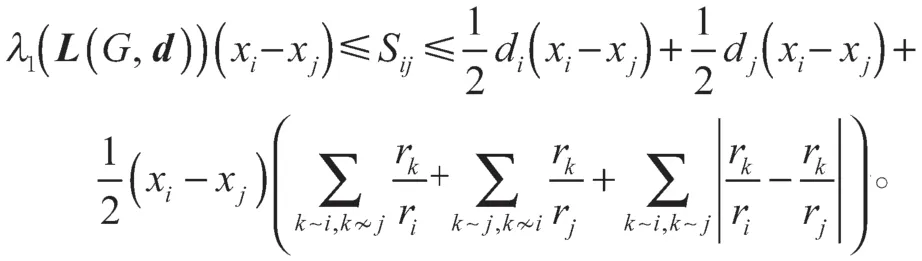
因为L(G,d)r=0，所以C(G)eT=0，C(G)的秩等于L(G,d)的秩。因eT、x是C(G)不同特征值的特征向量，所以向量x与eT正交。而xi＞xj，因此

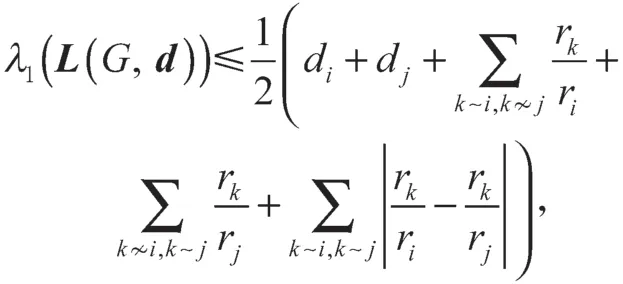
即L(G,d)最大特征值的上界为

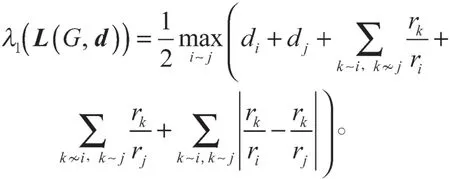
推论2设G是一个n阶连通图，(d,r)为G上的一个算术结构，则

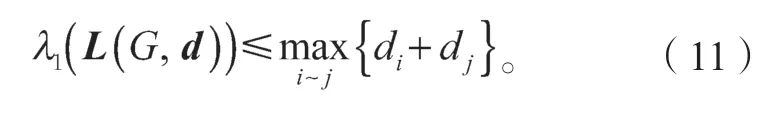
证明事实上

类似地可得

将上述两式子代入

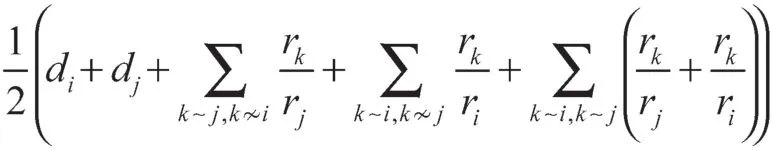
可得

即

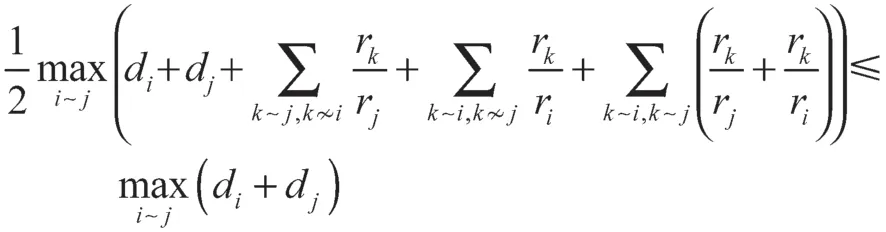
所以，由式（8）可知

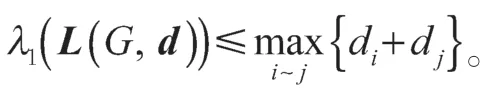
相比较而言，式（11）没有（8）精确，但计算简便一些，也可以作为判断特征值上界的一个依据。

4 算例

例1拆分完全图K4的边v3,v4得到的一个图S4，如图1所示。在G的算术结构的拉普拉斯矩阵L(G,d)中，若d=(1,2,10,15,1)T，r=(15,10,3,2,5)T，试用本文的结论计算L(G,d)的最大特征值的上界。

图1 图S4Fig.1 Figure S4

解用式（2）（4）（8）（11）计算得到L(G,d)的最大特征值的上界分别为35,20,15.5,17，而矩阵L(G,d)的实际特征值有5个，分别为0,0.891 2,2.600 8,10.293 0,15.215 0。

显然，由式（8）计算的结果为15.5，它与L(G,d)的实际最大特征值15.215 0相差非常小，所以式（8）更精确。

5 结语

本文得到了算术结构拉普拉斯矩阵L(G,d)的最大特征值的4个上界，分别如式（2）（4）（8）（11）所示，其中式（8）中的上界最精确，而式（11）中的上界计算较简便。