微型桩单桩抗弯承载力计算公式的推导及验证

，，

（1.湖南省交通科学研究院有限公司，湖南 长沙 410015； 2.湖南大学 土木工程学院，湖南 长沙 410082）

0 引言

微型桩一般是指桩径为70～300mm，长径比大于30，采用钻孔、强配筋和压力注浆工艺施工的灌注桩[1]。微型桩早期主要被用于地基加固中，近年来开始被用于边坡治理、滑坡修复和深基坑支护等工程实践中[2-5]。在边坡加固工程中，特别是滑坡等抢险工程中，微型抗滑桩能够快速施工，且与传统抗滑桩相比，对坡体的扰动很小，施工后桩体与岩土体共同受力，有利于调动岩土体自身的抗滑能力[6-10]。

国外有较多微型桩被用于加固滑坡、路堤及基坑等的成功案例[2-4]。国内王传甲[11]用两排微型桩和一排斜拉锚杆的复合结构治理安徽某滑坡。张玉芳[12]将微型抗滑桩群成功应用于加固京珠高速公路堑边坡。丁光文等[13]将微型桩复合结构成功用于鹰厦铁路路堑边坡病害治理工程。谢晓华[14]、高永涛[15]等也介绍并分析了微型桩在边坡加固方面的应用。

在微型桩加固边坡设计理论方面，抗弯承载能力及刚度是微型桩支护边坡的重要指标。微型桩的抗弯能力决定了桩体发生弯曲破坏的能力。而微型桩为柔性桩，微型桩发生弯曲破坏时必然伴随着较大的边坡下滑位移。可见，微型桩的抗弯承载能力是边坡安全评价的重要依据之一。因此，本文拟基于混凝土钢管桩抗弯承载力公式，推导两种不同配筋截面类型微型桩的抗弯承载力计算公式，并以数值验证其可行性，以期为微型桩在边坡加固工程中的设计和安全评价提供一定的理论参考依据。

1 微型桩单桩抗弯刚度及承载力计算

1.1 微型桩截面类型

微型桩由水泥砂浆体和加筋材料组成，加筋材料一般为钢管和钢筋，根据微型桩加筋情况的不同，常将微型桩截面形式分为如图1所示的两种类型。其中A型截面的加筋材料为钢管，B型截面的加筋材料由钢管和管内对称的3根钢筋组成。图中设计参数H为微型桩的桩径，h为钢管的外直径，s为钢筋截面形心到桩截面形心的距离。本文选用A型截面和B型截面两种截面类型进行研究。

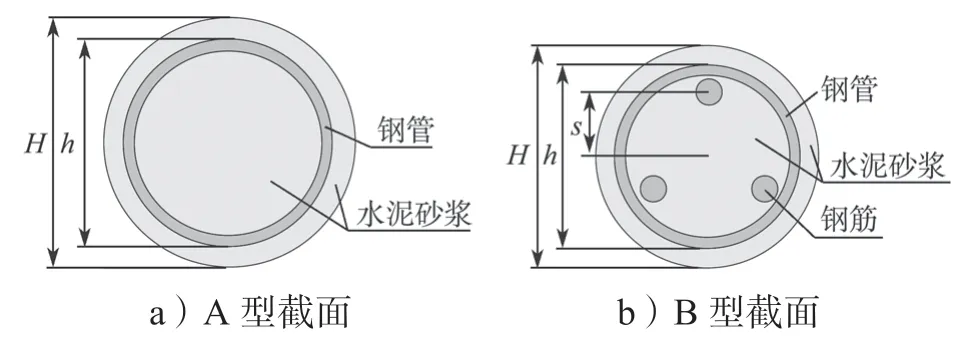
图1 微型桩的截面类型Fig.1 Section types of micro-piles

1.2 等效抗弯刚度计算

微型桩由水泥砂浆体和加筋材料组成，加筋材料一般为钢管和钢筋。按照微型桩抗弯刚度等效的原则求解微型桩的等效弹性模量，符合微型桩加固边坡的受力及变形特性，其等效弹性模量的计算公式如下：

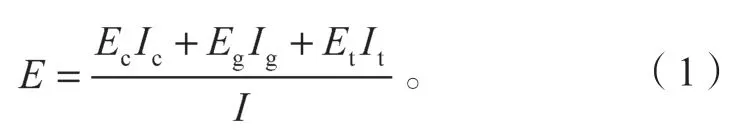
式中：E为微型桩等效弹性模量；

Ec为水泥砂浆浆体的弹性模量；

Eg为钢筋的弹性模量；

Et为钢管的弹性模量；

I为微型桩截面的惯性矩；

Ic为水泥砂浆浆体截面的惯性矩；

Ig为等效钢管的惯性矩；

It为钢管截面的惯性矩。

1.3 A型截面单桩抗弯承载力计算

本文的公式推导建立在文献[16]对钢管桩抗弯承载力的推导基础之上，考虑保护层浆体对抗弯承载力的贡献，并基于以下假定：

1）考虑钢管外侧受压区保护层浆体对抗弯承载力的贡献；

2）受压区保护层浆体不影响钢管内侧的受压区高度x；

3）受压区保护层的浆体全部受压屈服，且形状为弓形，弓形跨越的角度与钢管内侧受压区跨越的角度相同，如图2所示，图中x为受压区高度，α1为截面受压角度，r和R分别为钢管的内、外半径。

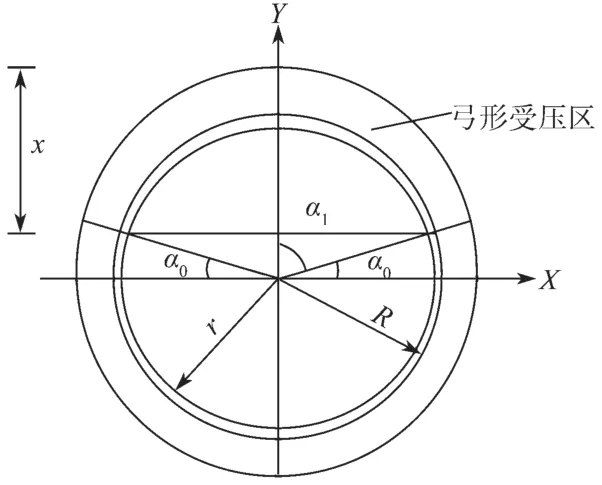
图2 截面受压区分布图Fig.2 Distribution of the section compression zones

1.3.1 弓形截面特性计算

截面受压角度α1的计算公式如下：

弓形形心位置的计算公式如下：

弓形面积计算公式如下：

式（2）～（4）中：H为桩径；

e为弓形形心至桩截面形心的距离；

Ae为弓形的面积；

α0的取值参考文献[16]，后同。

1.3.2 抗弯承载力公式

基于以上假定，由于假设偏于不安全，所以抗弯承载力的计算，在考虑钢管与核心浆体提供的承载力基础上，加上保护层受压区弓形对中性轴的弯矩，故最终的抗弯承载力表达式如下：

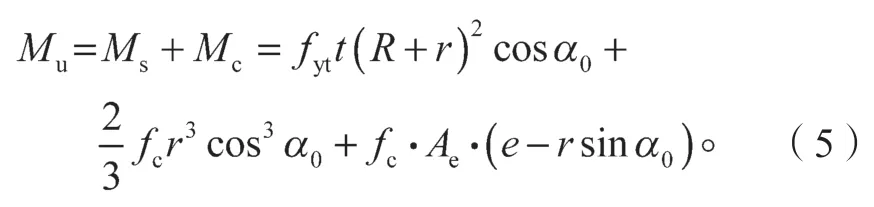
式中：Mu为微型桩的抗弯承载力；

Ms为钢材提供的抗弯承载力；

Mc为水泥砂浆体提供的抗弯承载力；

fyt为钢管的屈服强度；

t为钢管壁厚；

fc为水泥浆体的抗压屈服强度。

1.4 B型截面单桩抗弯承载力计算

B型微型桩截面的加筋体为钢管和3根钢筋，其截面形式与A型截面的不同之处是在钢管内部设置了3根钢筋，因此可以按照A型截面的设计方法进行设计。基于安全设计，对3根钢筋对抗弯承载力的贡献可按照最不利的抗弯形式进行计算，如图3所示，图中As为单根钢筋的截面积，σ、σ′为极限状态下钢筋所受到的拉应力和压应力。因此，基于A型截面抗弯承载力计算公式的推导，对钢筋的抗弯承载力做如下假定：

1）基于前文环形截面抗弯公式的推导；

2）截面的极限弯矩按照钢筋的最不利抗弯形式进行计算；

3）钢筋受力不影响受压区高度x；

4）钢筋的应力按照平截面假定进行计算。

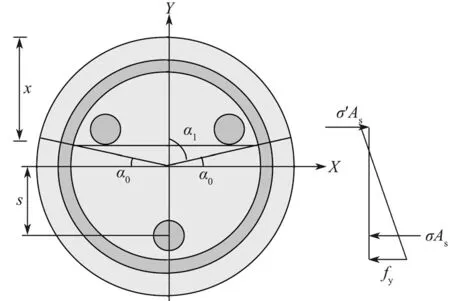
图3 最不利抗弯截面形式Fig.3 Most unfavorable bending section form

1.4.1 钢筋形心应力计算

受拉钢筋的应力σd计算公式如下：

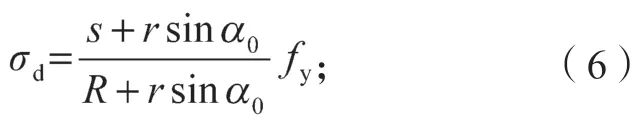
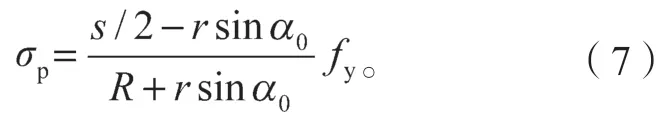
1.4.2 抗弯承载力计算

基于以上假定，并且由于假设偏于不安全，所以B型截面的抗弯承载力，为式（5）考虑的钢管与核心浆体以及保护层受压区弓形提供的承载力的基础上加上钢筋应力对中性轴的弯矩，故最终的抗弯承载力表达式如下：

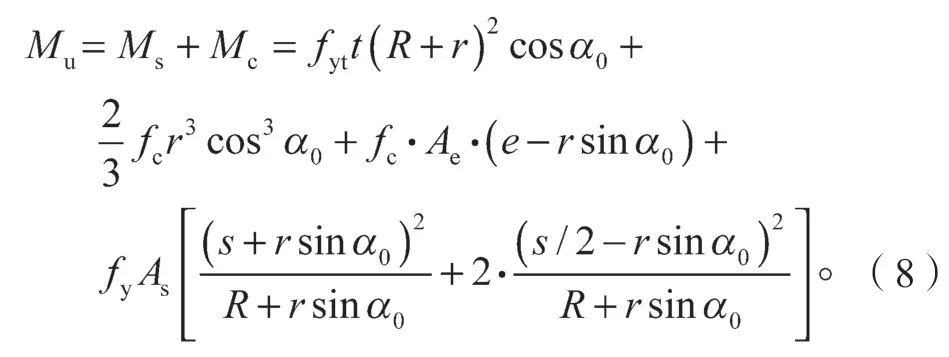
式中fy为钢筋的屈服强度。

2 单桩抗弯承载力的数值验证

2.1 抗弯承载力加载模型

数值验证时，采用3点加载形式进行抗弯承载力的模拟，加载的力学模型见图4。

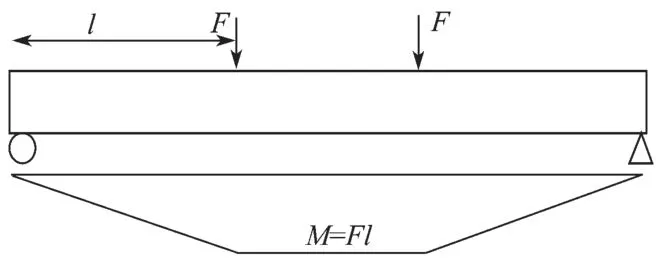
图4 抗弯加载力学模型Fig.4 Mechanical model of flexural loading

图4所示模型为简支梁受对称荷载作用，跨中的截面处于纯弯曲状态且弯矩最大，由于力学模型对称，故简化后取力学模型的一半进行模拟。因此，通过逐级增加荷载F直至桩发生弯曲破坏，得到桩所能承受的最大弯矩即为桩的抗弯承载力。

2.2 材料参数取值

采用FLAC3D有限差分软件对两个典型截面进行抗弯承载力数值模拟验证，截面类型分别为100-A和200-B，截面特性取值情况见表1。

表1 微型桩截面特性取值Table 1 Characteristic values of micro-piles mm

材料数值模型均采用摩尔库伦模型，钢筋和钢管的材料性质一致，以钢材和水泥浆体的抗拉强度、抗压强度反算出摩尔库伦模型的内摩擦角和黏聚力[17]，所有参数取值见表2。

表2 数值模型参数取值Table 2 Parameter values of numerical models

在数值模型中，钢管、浆体、钢筋三者之间均设置了不考虑厚度的接触单元，接触模型采用能够考虑拉伸破坏的库伦剪切滑移模型。其中，法向刚度与切向刚度对计算结果的影响不大，故主要根据钢材和水泥浆体刚度确定，将法向刚度kn和切向刚度ks均取3×1012N/m。为避免数值模拟破坏模式与解析结果假设的破坏模式相差过大，设置界面抗拉强度与浆体抗拉强度的取值相同，均为4 MPa，界面的抗剪强度则取为其抗拉强度的2倍，即为8 MPa。

2.3 100-A型截面抗弯数值验证

2.3.1 逐级加载数值试验结果

100-A截面特性以及加载方式如图5所示。荷载分别取4,14,18 kN时，桩体单元的屈服状态以及左端截面的应力分布如图6所示。

图5 100-A截面特性及加载方式Fig.5 100-A section characteristics with its loading method

由图6可以得知，荷载较小时，水泥砂浆浆体被拉裂，随后受压区的水泥砂浆浆体开始受压屈服，之后受拉区的钢管也开始屈服，并且随着荷载的不断增加，水泥砂浆浆体与钢管的屈服范围逐渐向桩心扩大，直至被破坏。整个试验过程中，左端截面的位移随着荷载的增加而逐渐增大，当达到破坏荷载时，位移趋向于不收敛。数值试验全过程的荷载-挠度曲线如图7所示。

2.3.2 理论公式计算结果与数值试验结果对比分析

由图6可知，钢筋受拉屈服时应力为230 MPa，受压屈服应力为206 MPa，均与理论值235 MPa接近，并且水泥砂浆浆体的屈服应力也接近于其屈服强度（40 MPa）。也就是说，数值试验对材料的力学性能方面的模拟相对合理。根据试验数据，大致可以得出微型桩的极限荷载为18 kN，此时所对应的极限弯矩为7.2 kN·m，而通过理论公式（5）计算出的极限弯矩为7 kN·m，这一结果说明理论公式计算所得的抗弯承载力偏安全，并且与数值验证结果很接近。因此，式（5）所示的理论公式计算符合工程要求，可予以采用。

2.4 200-B型截面抗弯数值验证

2.4.1 逐级加载数值试验结果

200-B截面特性以及加载方式如图8所示。荷载分别取40,80,115 kN时，桩体单元的屈服状态以及左端截面的应力分布如图9所示。

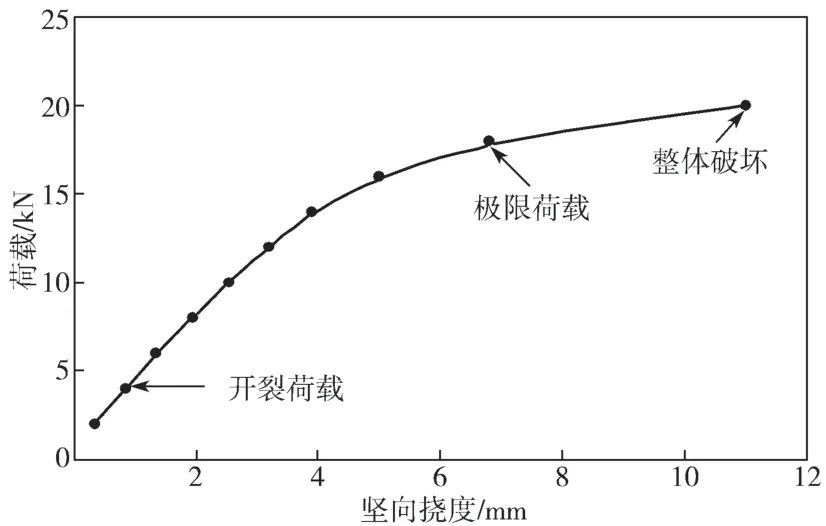
图7 100-A型微型桩荷载-挠度曲线Fig.7 100-A typed micro pile load deflection curve

图8 200-B截面特性及加载方式Fig.8 200-B section characteristics with its loading method

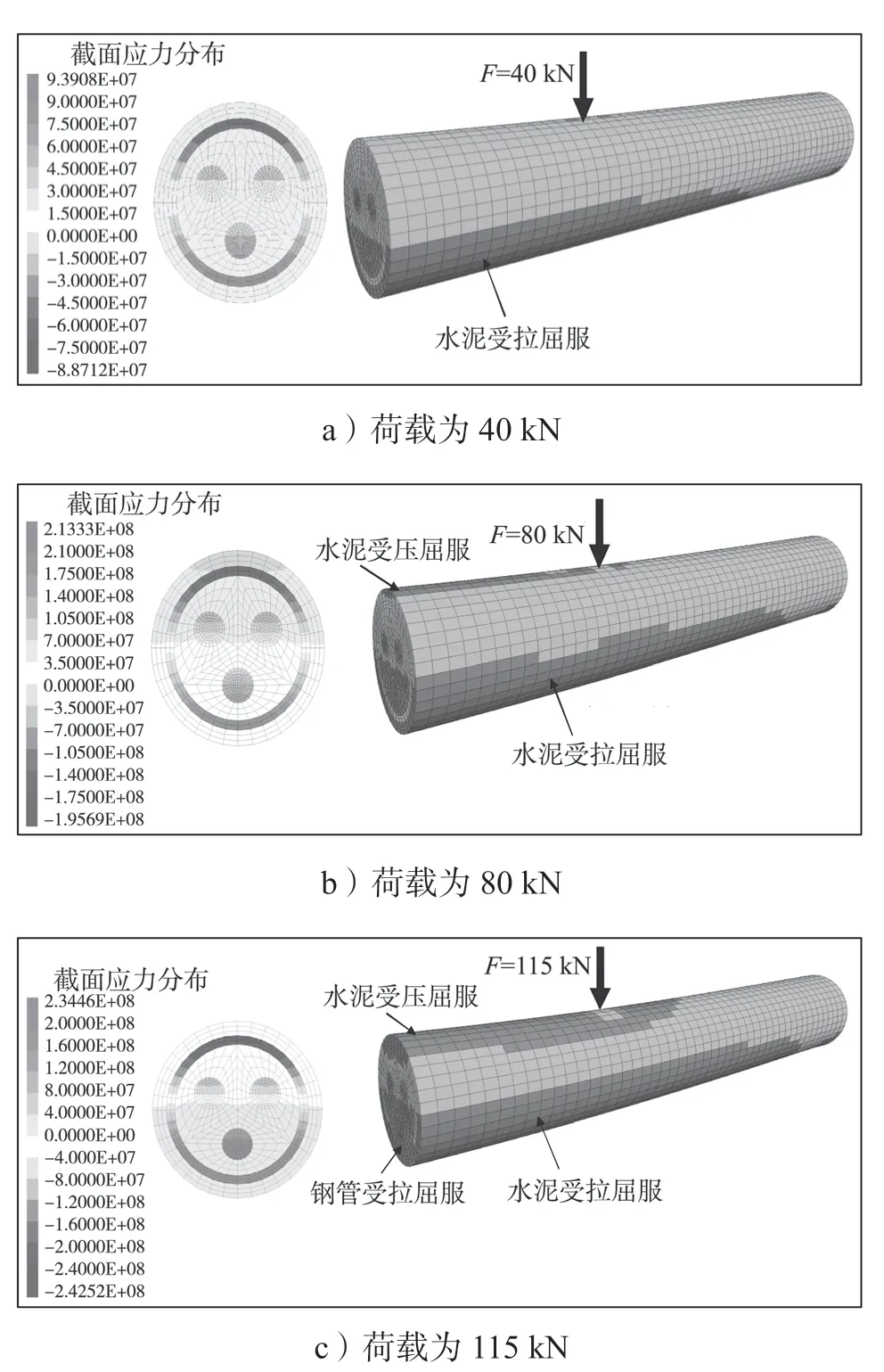
图9 不同荷载时的屈服状态及截面应力分布Fig.9 Yield state and section stress distribution under different loading values

由图9可以得知，荷载较小时，水泥砂浆浆体被拉裂，随后受压区的水泥砂浆浆体开始受压屈服，之后受拉区的钢管也开始屈服，并且随着荷载的增加，水泥砂浆浆体与钢管的屈服范围逐渐向桩心处扩大，直至被破坏。在破坏状态，受拉区钢筋应力接近屈服应力且部分已经屈服；受压区的钢筋始终未屈服，但是其边缘的应力接近屈服应力。整个加载过程中，左端截面的位移随着荷载逐渐增大，达到破坏荷载时，位移趋向于不收敛。数值试验全过程的荷载-挠度曲线如图10所示。

图10 200-B型微型桩荷载-挠度曲线Fig.10 200-B type micro pile load deflection curve

2.4.2 理论公式计算结果与数值试验结果对比分析

由图9可知，钢筋受拉屈服时的应力为235 kPa，受压屈服时的应力为243 kPa，均与理论值235 kPa很接近，并且水泥砂浆浆体的屈服应力也接近于其屈服强度40 kPa。也就是说，数值试验对材料的力学性能方面的模拟相对合理。根据试验大致可以得出极限荷载为115 kN，此时所对应的极限弯矩为92 kN·m，而通过式（8）算出的极限弯矩为88.4 kN·m，两者较为接近，说明式（8）所计算的抗弯承载力偏安全，且与数值验证结果很接近，满足工程要求。

3 结论

本文基于混凝土钢管桩抗弯承载力公式，推导了两种不同配筋截面类型微型桩的抗弯承载力计算公式，并通过3点加载的数值试验验证了微型桩抗弯承载力计算公式。

单桩抗弯承载力的数值验证结果表明：

1）A型截面钢筋受拉屈服时的应力计算值为230 MPa，受压屈服时的应力为206 MPa，十分接近理论值235 MPa；数值试验的极限弯矩为7.2 kN·m，与理论公式的计算值7 kN·m十分接近，这一结果证明了假设的合理性以及抗弯承载力公式的可行性。

2）B型截面钢筋受拉屈服时的应力计算值为230 kPa，受压屈服时的应力为206 kPa，均小于理论值235 kPa；数值试验的极限弯矩为92 kN·m，与理论公式的计算值88.4 kN·m接近，这表明该结果偏安全且满足工程要求，不仅证实了偏安全的假设条件，同时说明了抗弯承载力公式的可行性。

以上结论可为微型桩在边坡加固工程中的设计和安全评价提供理论依据。