典型双坡低矮建筑屋面局部风压非高斯特性研究

，， ， ，

（1.结构抗风与振动控制湖南省重点实验室，湖南 湘潭 411201；2.湖南科技大学 土木工程学院，湖南 湘潭 411201；3.湖南百利工程科技股份有限公司，湖南 岳阳 414000）

1 研究背景

我国东南沿海的农村住宅主要为低矮建筑，其高度一般不超过24 m，位于大气边界层的最下层区域，该区域的风场特性受地形起伏和周围建筑物的影响较大。风场中贴近地面的区域，因受地面粗糙程度的影响，气流紊乱程度增加，从而导致作用于建筑表面风压时程的脉动幅值间歇性显著。有研究表明[1]，此时建筑所受的风压时程并不符合Davenport假设，而表现为明显的非高斯特性。

大量灾后调查结果表明，低矮建筑的破坏主要是屋面破坏，且主要集中在屋檐、屋脊和角部等区域。而这些区域的气流特性复杂，因此有必要对双坡低矮建筑屋面在这些区域风压的非高斯特性进行研究。

国外已有学者对风压的非高斯特性进行了研究。如K.S.Kumar等[2]基于快速傅里叶变换，对低矮建筑非高斯风压时程进行了模拟，并且将结果与不同屋面类型在不同条件下非高斯风压数据进行对比，证实了模拟方法的有效性。F.Sadek等[3]基于实验数据，对低矮建筑表面的非高斯峰值风压进行了研究，提出了设计上可以采用的非高斯风压极值估计方法。A.Kareem等[4]利用数值模拟方法，对比分析了不同计算模型和分析方法对湍流作用下低矮建筑表面风压的非稳态、非高斯、非线性等特性研究的可行性和效果。Ko N.H.等[5]研究了方形建筑侧面风压的非高斯特性，同时对高斯风压时程和非高斯风压时程进行了模拟，并将模拟结果与实测数据进行对比，分析了非高斯风压对方形建筑侧面风荷载的影响。

国内也有部分学者对风压的非高斯特性进行了相关研究。如王旭等[1]利用超强台风现场实测和风洞实验相结合的方法，分析了低矮建筑屋面部分区域风压的非高斯特性。韩宁[6]、楼文娟[7]、庄翔[8]等分别基于风洞实验，对不同体型的高层建筑的迎风面和侧面风压的非高斯特性进行了分析，一致得出在侧面迎风等气流分离程度大的区域非高斯性更加显著的结论。罗颖等[9]探讨了低矮建筑在不同屋面坡度、风向角、高度及地貌条件下屋面风压特性的变化，分析了峰值因子的变化规律以及非高斯区分布特点理论，并且给出了峰值因子的简化计算式。

本研究拟利用风洞试验，对A、B、C 3类地貌风场下典型双坡低矮建筑屋面风压非高斯特性展开研究，并结合屋面风压空间相关性对低矮建筑屋面流场特性与屋面风压非高斯特性的关系进行阐述，给出屋面局部区域非高斯风压的产生原因，以期为低矮建筑围护结构抗风设计提供一定的参考。

2 风洞试验概况

2.1 试验设备及流场模拟

本研究的风洞试验，在湖南科技大学风工程试验研究中心大气边界层直流式风洞中完成，试验采用的测压系统包括PSI电子压力扫描阀系统、三维脉动风速仪、皮托管和装有PSI采集软件的电脑。

利用尖劈、挡板、粗糙元等被动模拟装置，模拟出符合我国规范[10]规定的1:20缩尺比例的低矮建筑风洞试验A、B、C 3类地貌风场，其平均风速剖面指数α分别为0.12,0.15,0.22。各风场的风速剖面、湍流度剖面模拟结果见图1。由图1可以得知，平均风速剖面曲线符合GB5009—2012设计规范，湍流强度剖面理论曲线参考日本规范计算方法给出。A、B、C 3类地貌风场参考高度处对应的名义湍流度分别为12.2%,13.8%,23.2%。图1中Hr为参考高度，Iu和Ur分别为参考高度处的湍流度和风速，风洞试验布置方式如图2所示。

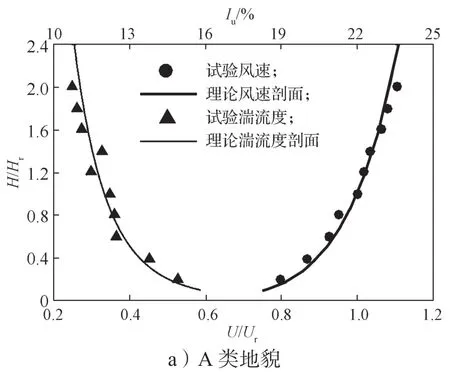
图1 风场模拟结果Fig.1 Wind field simulation results

图2 风洞试验布置图Fig.2 Test wind tunnel test layout

2.2 试验模型及测点布置

风洞测压刚性模型采用ABS（Acrylonitrilebutdiene-styren）板制作，满足试验所需要的刚度要求，模型按几何缩尺比例为1:20进行设计，风速缩尺比例设定为1:1，所以时间缩尺比例为1:20，试验风速为10 m/s。模型的平面尺寸为600 mm×400 mm，屋檐高度为400 mm，屋面坡角为18.4°，房屋缩尺模型如图3所示。本文试验模型的阻塞率为3%，满足风洞试验阻塞率小于5%的要求。屋面上采用对称方式共布置了130个测点（见图3和图4）。为了方便研究与叙述，本研究选择在迎风屋面的角部、屋脊、屋檐等局部测点进行区域划分，具体分区见图4。

图3 低矮房屋缩尺模型图Fig.3 Scale model of low-rise buildings

图4 屋面测点布置与分区示意图Fig.4 Layout and division diagram of roof measuring points

2.3 试验数据处理方法

本研究中，测压信号的采样频率为332.5 Hz，采样时间为30 s，对应的实际建筑采样时间为10 min，满足GB 50009—2012《建筑结构荷载规范》[10]中规定的不小于10 min的要求，试验中每个测点采样个数为10 000个。风压系数定义为风作用于建筑表面的实际压力与来流风压的比值[11]，本文以模型屋面平均高度处风压作为无量纲化的参考风压，定义风压系数Cpi(t)计算式如下：

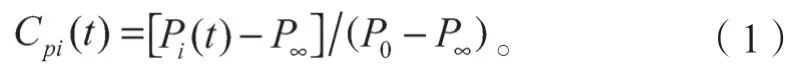
式中：Pi(t)为第i测点处风压值；

P0和P∞分别为参考高度处总压和静压。

风压的非高斯特性通常采用风压系数时程的偏度和峰度来描述，二者是判别风压时程高斯与非高斯分布的2个重要参数。偏度值和峰度值的计算公式参考文献[12]给出。

为了研究屋面特征湍流对风压非高斯特性的影响，可以通过分析不同测点间风压系数的互相关性进行阐述，引入互相关系数ρxixj，定义如下：

式中：xi、xj分别为测点i和j的风压系数序列；

Exi和Exj分别为xi、xj对应的数学期望；

σxi和σxj分别为xi、xj对应的标准差。

3 风压时程的概率分布

为研究屋面的风压概率分布特性，基于18.4°坡角屋面测点风压时程数据，本研究采用Gaussian分布、三参数Gamma分布、三参数对数正态分布、广义极值分布（generalized extreme value distribution，GEV）4种分布方式，对屋面的典型测点风压时程进行拟合分析。得到的B类地貌工况中45°风向角作用下迎风屋面的典型测点的风压系数概率密度分布拟合结果如图5所示。

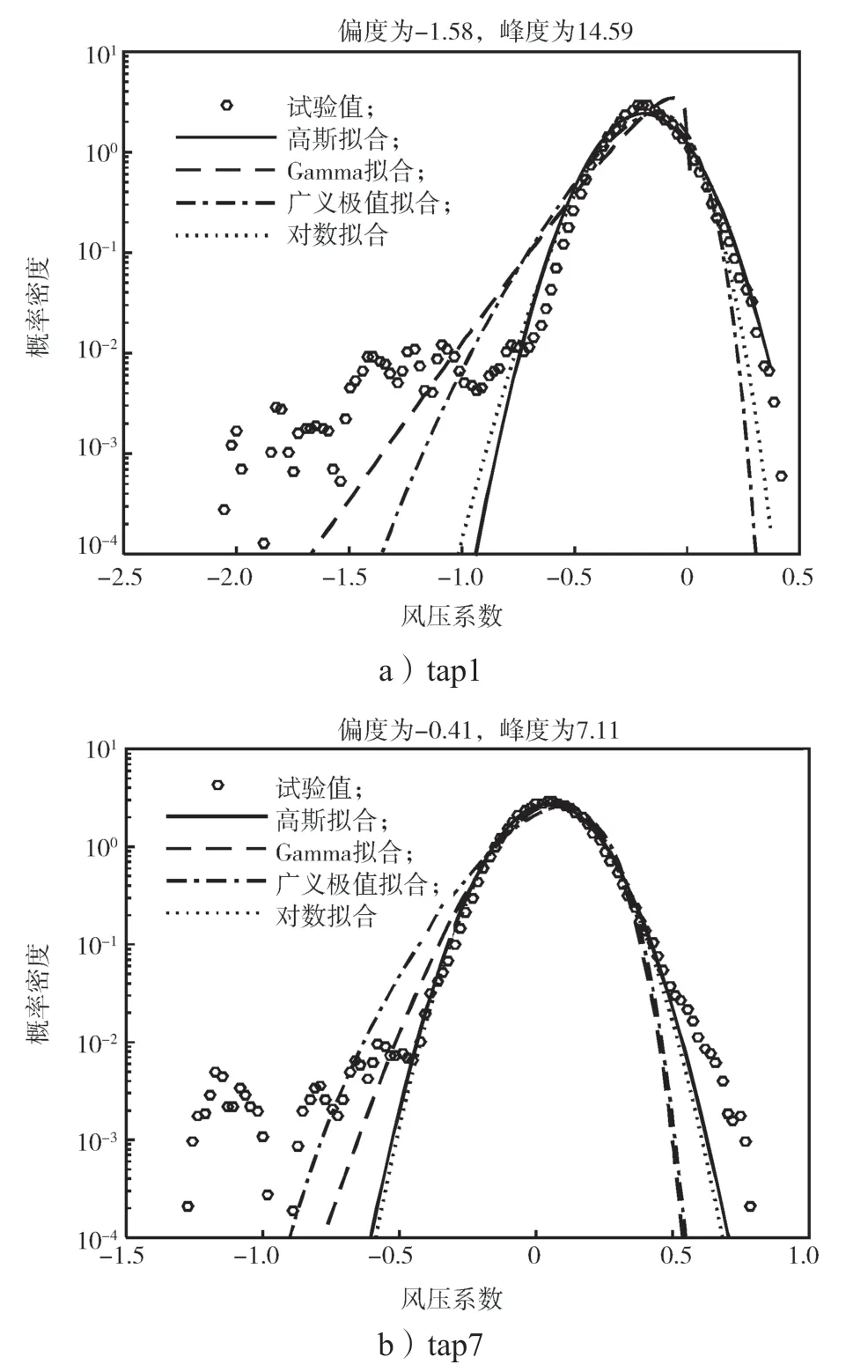
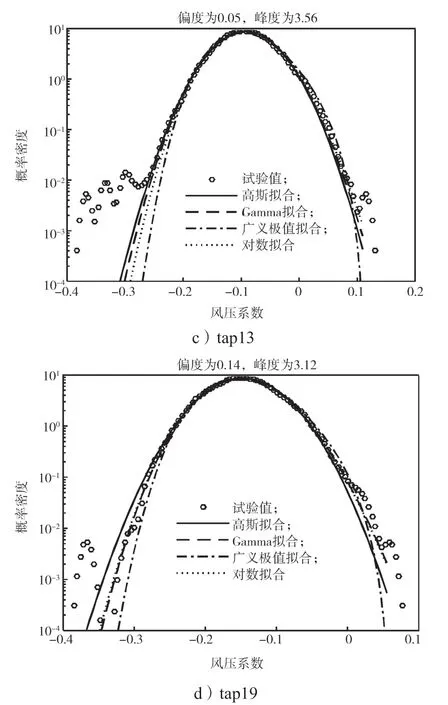
图5 45°风向角下迎风屋面典型测点的风压系数概率密度曲线Fig.5 Probability density of wind pressure coefficients for typical taps on windward roof under 45°wind angle

如图5所示，测点1和7处于屋盖角部区域，风压系数受锥形涡影响较大，导致其统计特性偏离了高斯分布且都为负偏斜，从统计学上说明此区域实际风吸力出现的概率比高斯假设更大，更易遭到破坏；其中，Gamma分布和广义极值分布（GEV）对斜风向角部区域测点风压时程概率分布拟合程度更高，但是对于高峰度的长拖尾区域很难进行较优拟合。而测点13和19位于迎风屋盖中部，锥形涡发展到此区域时其截面增大，涡旋强度减弱[13]，因而两者的风压系数概率密度分布曲线更接近高斯分布。此时测点13风压时程的偏度和峰度分别为0.05和3.56，测点19的分别为0.14和3.12，均接近高斯分布下的理论偏度值0和峰度值3。同时发现随着与屋面角部区域距离的增加，负偏斜拖尾长度减小。

4 屋面风压非高斯性分区

本节通过改变来流风向角和地貌类型研究低矮双坡建筑风压非高斯特性分区特点。理论上高斯分布的偏度与峰度值分别为0和3，但由于风场紊流的随机性导致实验过程中绝对的高斯分布很少见，因此，综合相关研究[14-15]，文中采用|S|＞0.5且|K|＞3.5作为风压高斯区与非高斯区划分的标准。

4.1 不同风向角下非高斯性风压分布

通过分析B类地貌下建筑受风向角分别为0,20,30,45,60,90°时屋面非高斯区的分布特点，描述风向角对双坡低矮建筑屋面非高斯分区的影响。B类地貌下屋面非高斯区域随风向角的变化分布如图6所示，图中实心点处风压表现为高斯性，而空心点处为非高斯性。

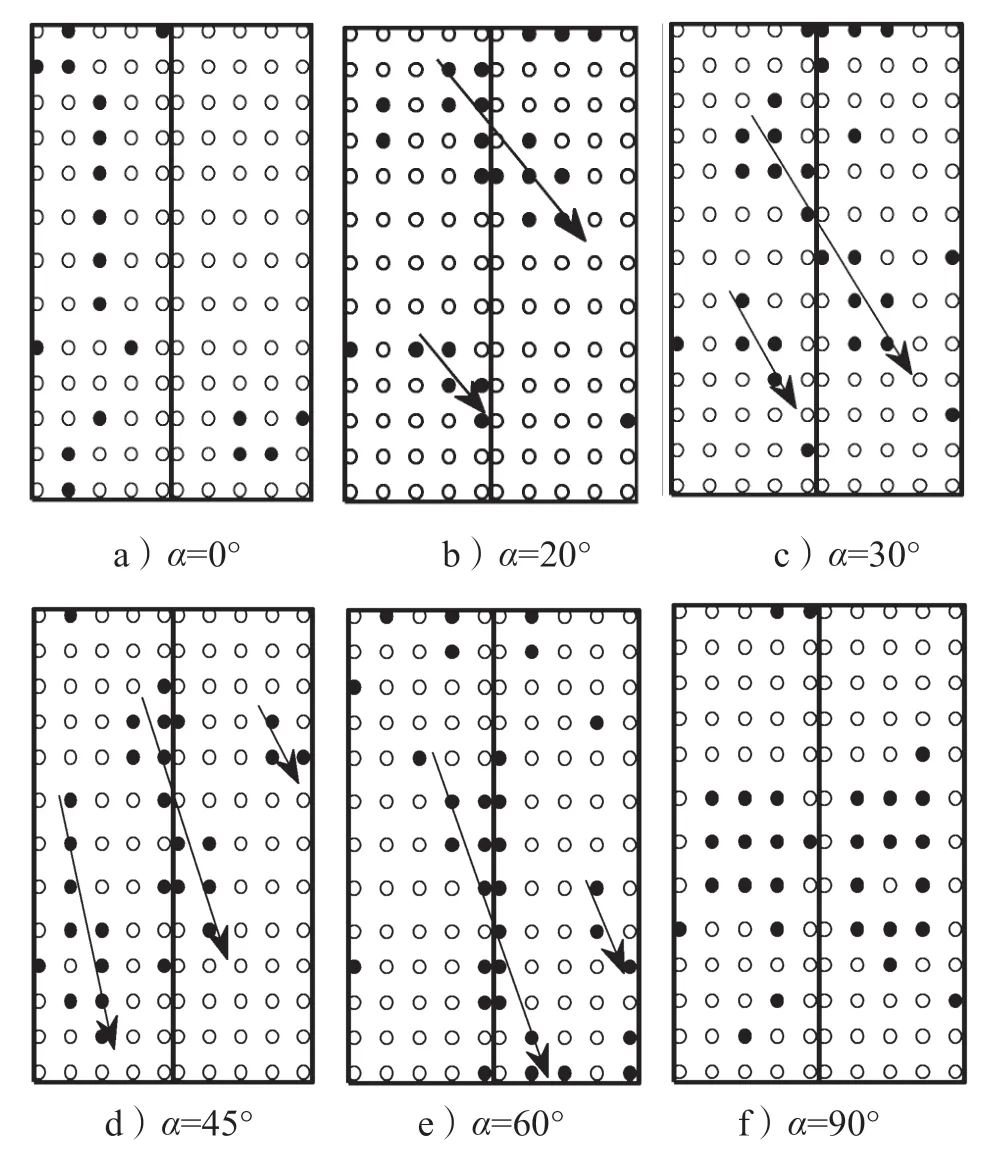
图6 屋面非高斯区域随风向角变化分布Fig.6 Distribution of non-Gaussian area on roofs under various wind angles

由图6可知，风向角对非高斯区分布影响显著，特别是斜风向角作用下（如风向角为20°,30°,45°,60°），高斯区分布大体与风向角一致，如图中箭头所示。而非高斯区则主要分布在高斯区两侧，这是因为来流风在经过屋角区域后因气流分离形成两股锥形涡并沿着来流方向向前发展所致[16]。处于锥形涡作用范围的测点受气流涡旋影响较大而导致风压非高斯性显著，两股涡的中间区域风压由于旋涡的相互干扰反而表现为高斯性。

0°风向角下，屋面大部分测点表现为非高斯性，高斯风压区主要集中在迎风屋盖第3排测点范围，这是因为来流直接作用于迎风屋盖的中部区域，而此区域受屋檐和屋脊区域的气流分离影响较小。

90°风向角下，非高斯区则主要分布在前后山墙区、两侧屋檐区以及屋脊区，这是由于气流在迎风前缘区分离产生旋涡脱落而在来流下游区再附所致；两侧屋檐区受建筑绕流影响较大而表现出明显的非高斯性。

4.2 不同地貌下非高斯性风压分布

图7～9给出了18.4°坡角双坡低矮建筑在A、B、C 3类地貌下受来流风向角分别为0,45,90°时的屋面非高斯区分布。

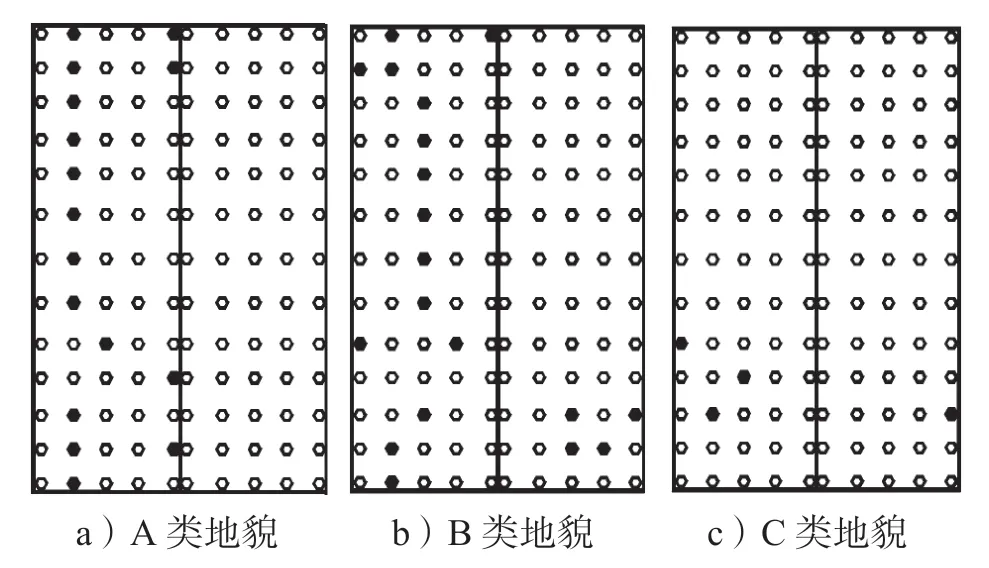
图7 不同地貌中0°风向角下非高斯区分布Fig.7 Distribution of non-Gaussian area under 0°wind direction angle in different landforms

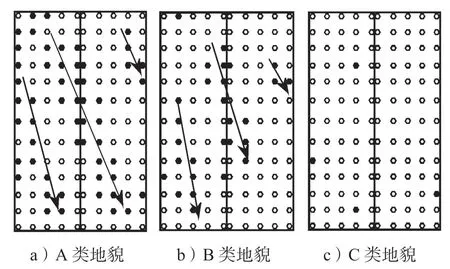
图8 不同地貌中45°风向角下非高斯区分布Fig.8 Distribution of non-Gaussian area under 45°wind angle in different landforms

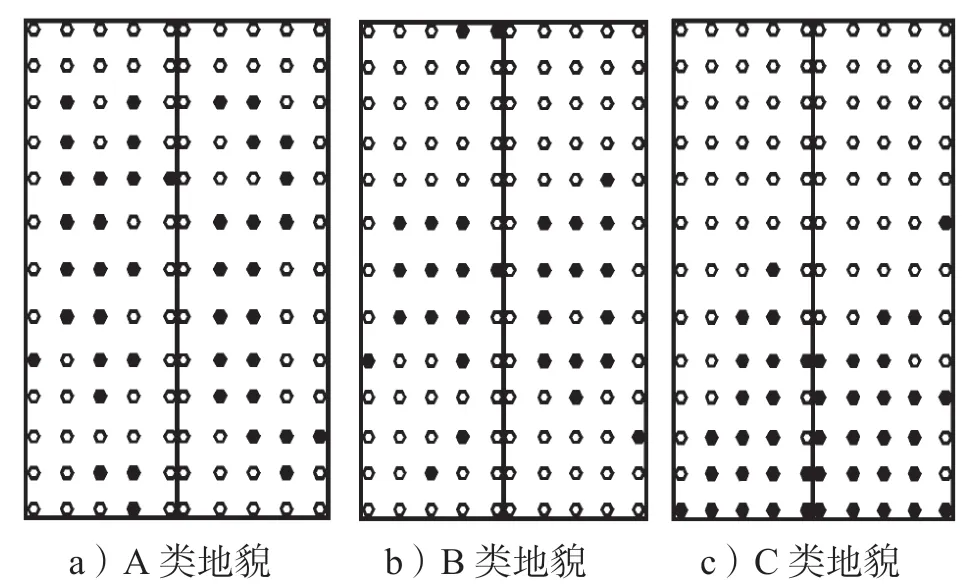
图9 不同地貌中90°风向角下非高斯区分布Fig.9 Distribution of non-Gaussian area under 90°wind angle in different landforms

非高斯区的分布特点说明了地貌类型对双坡低矮建筑屋面非高斯区分布规律的影响，从图7～9中可以看出，18.4°坡角的双坡低矮建筑在相同的风向角作用下，地貌类型对屋面非高斯区的分布影响显著，具体描述如下。

如图7所示，0°风向角下，A类地貌下高斯区测点分布位置较B类地貌的更靠近迎风屋檐，这是由于A类地貌中来流湍流度较小，屋檐区域处产生的气流分离程度相对较小；当建筑处于来流更为复杂的C类地貌下时，几乎屋面所有的测点风压均表现为非高斯性。

如图8所示，45°风向角下，在A、B地貌类型中，表现为高斯性的测点主要沿来流方向按箭头方向呈三股区域分布，结合文献[17]中对斜风向作用下低矮建筑屋面锥形涡的分布特点进一步说明此结论。从A类地貌到B类地貌，三股高斯区域沿来流方向移动，且区域范围有所减小，这是因为在B类地貌中屋面锥形涡气流影响范围扩大所致。

如图9所示，90°风向角作用下，不同地貌中两侧屋盖非高斯测点区域分布基本对称，体现了实验数据的合理性。从A类地貌到C类地貌，高斯区域沿来流方向逐渐向前移动，这是由于随着来流湍流度增大，在气流分离区旋涡脱落加剧，导致分离区非高斯区域范围越来越大。同时发现，A类地貌和B类地貌中，在屋面来流下游靠近山墙区域出现较大范围的非高斯测点，这是由于分离气流在此区域产生再附和建筑尾流的卷吸作用所致。

5 局部非高斯风压与屋面流场特性的关系

5.1 屋面风压非高斯性变化规律

图10和图11分别给出了18.4°坡角屋面，在0°风向角作用下，顺风向测点风压偏度变化曲线和峰度变化曲线。

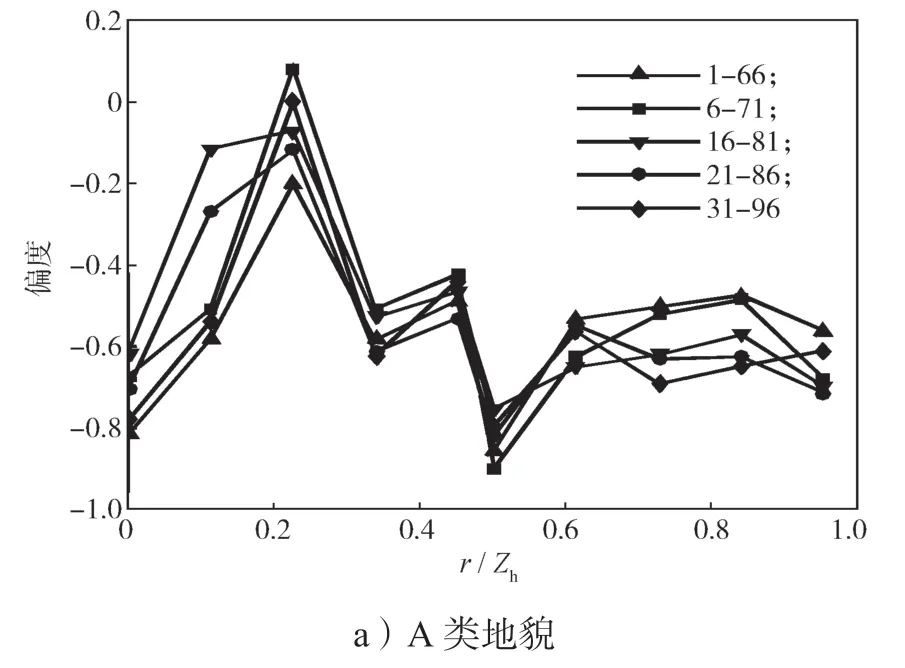
图10 不同地貌中0°风向角作用下顺风向测点风压偏度变化曲线Fig.10 Curves of skewness change under a wind direction angle of 0°

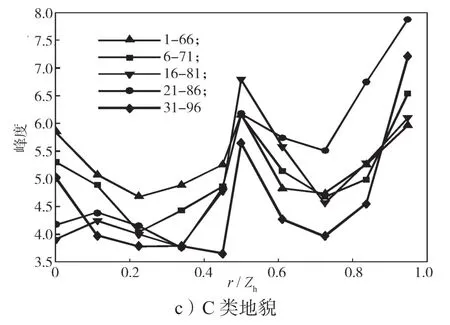
图11 不同地貌中0°风向角作用下顺风向测点风压峰度变化曲线Fig.11 Curves of kurtosis change under a wind direction angle of 0°

图10和11中各曲线图标分别代表相关性计算参考点和所考察目标测点序列的最后点，横坐标表示屋面测点距离与屋檐高度的比值，图12、13同。

从图10所示不同地貌中0°风向角作用下顺风向测点风压偏度曲线和图11所示不同地貌中0°风向角作用下顺风向测点风压峰度变化曲线的变化趋势来看，不同地貌下偏度的变化趋势大体一致呈“M”形，且整体呈现出下降的态势；而峰度曲线则呈现出“W”形的变化趋势，且整体呈上升趋势。这一结果，一方面说明偏度与峰度一般表现为明显的不同步性；另一方面，说明小偏斜高峰态以及大偏斜低峰态出现的概率较低。从偏度极值与峰度极值出现的位置来看，不同地貌类型下，迎风屋面约0.2倍屋檐高度处的风压偏度和峰度均出现了较明显的极值点，表现为极小偏度（绝对值）和峰度，非高斯性最弱；在屋脊位置（0.5倍屋檐高度）附近，风压偏度和峰度大多出现了第二个明显的极值点，表现为较大的偏度（绝对值）和峰度，非高斯性显著增强，但是C类地貌中偏度的极大值（绝对值）点出现在0.6倍屋檐高度处（即背风屋脊处），这不排除是实验误差所致。另外，发现屋面的第4排、第5排测点（迎风屋面靠近屋脊的两排测点）的风压偏度值，在C类地貌中没有出现类似于A、B类地貌中先下降后上升的变化过程，而是表现为平缓地下降。

5.2 屋面流场特性的相关性分析

本节将从风压空间相关性着手分析屋面风压非高斯特性的分布规律，已有的相关研究结果表明，产生大尺度旋涡的区域一般表现为风压空间相关性较强[15]，互相关性系数可以用于衡量任意两个测点在一定时间序列下取值的相关性程度，统计学上通常认为相关系数绝对值大于0.5时两者为强相关，而当相关性系数绝对值小于0.2时，则视为弱相关。0°风向角下，顺风向测点风压空间相关性曲线如图12所示，0°风向角下横风向测点的风压空间相关性曲线如图13所示。

图12 0°风向角下顺风向测点风压空间相关性曲线Fig.12 Curves of wind spatial correlation of downwind direction point under a wind direction of 0°

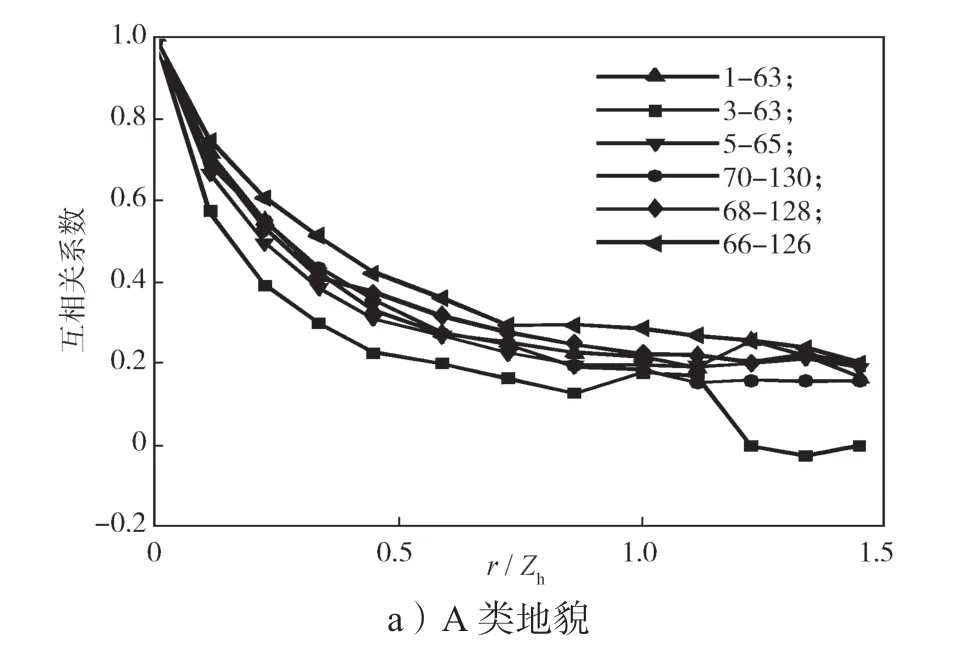
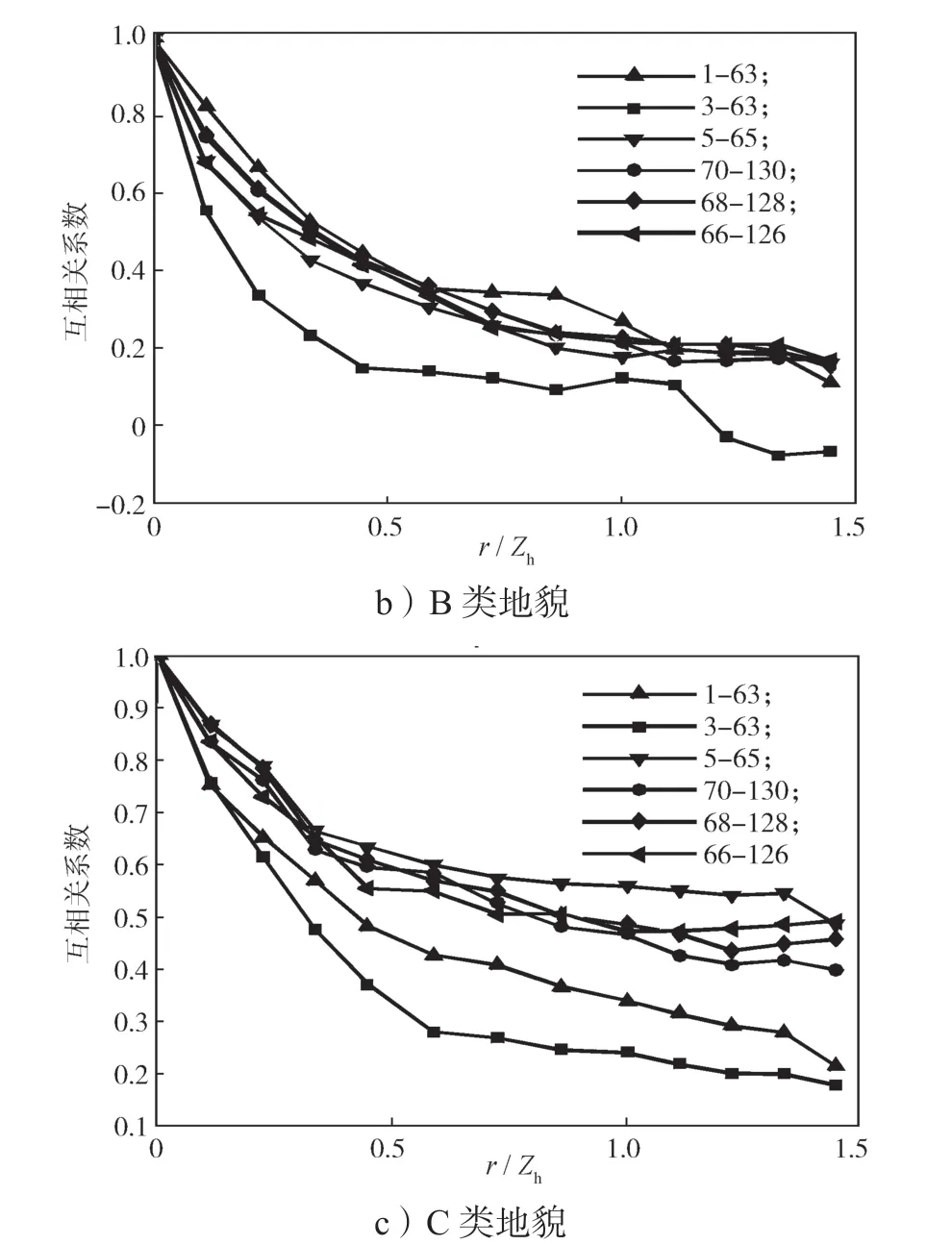
图13 0°风向角下横风向测点风压空间相关性曲线Fig.13 Curves of wind spatial correlation of cross wind points under a wind direction of 0°

图12和13仅给出了0°风向角下的测点风压空间相关性结果，由图可知，屋面受0°风向角作用时，不同地貌下顺风向和横风向各列测点风压相关系数的变化趋势基本一致。由图10可知，迎风前缘区测点风压的相关性最强，风压非高斯性最强，在约0.2倍屋檐高度处风压相关性达到最弱相关，之后测点风压相关性增大，在屋脊区域附近达到另一个峰值，背风屋盖区测点风压相关性相比于屋脊略有衰减。由图13可知，横风向相关性曲线基本符合负指数率模型，与顺风向风压相关性曲线的差别较大；不同地貌下位于约0.2倍屋檐高度处的3～63测点序列相关性最弱，结合横风向测点相关性规律，说明屋面上约0.2倍屋檐高度处受特征湍流[18]的影响最小，非高斯特性最弱。同时结合图10和11可以看出，C类地貌下各测点序列相关性明显较其他两类地貌下的强，这是由于C类地貌下来流风脉动性更强，导致屋面测点间的风压相关性增强。

综合上述分析，发现风压相关性曲线波动与偏度和峰度变化趋势具有明显的关联规律：风压相关性较弱的区域偏度和峰度都较小，而风压相关性较强的区域偏度和峰度较大。这一结论说明屋面风压非高斯性与屋面气流的相互作用呈正相关，这与文献[12]中的结论一致。通过分析屋面测点风压的相关性，可以了解典型双坡屋面风压的非高斯性分布特点。

6 结论

通过对坡角为18.4°的典型双坡低矮建筑在不同地貌下进行风洞试验，并对屋面典型测点风压时程进行概率密度拟合，分析屋面非高斯风压区分布特点及屋面局部风压非高斯特性与屋面流场的关系，得出如下结论：

1）斜风向作用下，风压非高斯特性显著，而对于距迎风角部较远的测点风压更加接近高斯分布。斜风向下Gamma分布和广义极值分布（GEV）对迎风角部测点风压时程概率分布拟合效果更优，但是对于高峰度的长拖尾区域仍很难进行较优拟合。

2）高斯区测点分布随风向角的改变而变化，非高斯性测点由于受锥形涡外围影响而分布在其两侧；0°风向角下，高斯区主要分布在垂直来流方向第3排测点；90°风向角下，非高斯区分布于迎风山墙的气流分离区和背风山墙气流再附区。

3）0°风向角下，随着来流湍流强度的增大，高斯区分布沿来流方向前移；45°风向角下，A、B两类地貌中高斯性测点主要沿来流方向分成三股区域，且由A类地貌变化到B类地貌时，该高斯区域沿来流方向发生移动，且区域范围缩小。

4）不同地貌下，偏度变化大体呈“M”形变化趋势，整体呈下降态势；而峰度呈“W”形变化趋势，整体呈上升趋势，偏度与峰度具有明显的不同步性。风压相关性曲线波动与偏度和峰度变化趋势具有明显的相关联规律，相关系数大的区域，风压的非高斯特性更显著。