基于C1自然邻近插值的曲面拟合

聂志峰， 周慎杰， 王 凯， 孔胜利

（1. 山东大学机械工程学院，山东 济南 250061；2. 山东科技大学机械电子工程学院，山东 青岛 265510）

基于C1自然邻近插值的曲面拟合

聂志峰1,2， 周慎杰1， 王 凯1， 孔胜利1

（1. 山东大学机械工程学院，山东 济南 250061；2. 山东科技大学机械电子工程学院，山东 青岛 265510）

以C0连续non-Sibsonian 插值作为三次单纯形Bernstein-Bézier多项式的基坐标，构造C1连续自然邻近插值函数。介绍了高阶连续函数的构建原理和性质。将C1连续自然邻近插值函数应用于曲面拟合场合，由于Voronoi图能够自动调整数据点分布不规则和密度不均匀在空间上的差异，即使对于散乱数据点，也能获得较好的拟合结果。

计算机应用；曲面拟合；C1自然邻近插值；Bernstein-Bézier多项式

对于规则网格数据点的插值问题，通常采用样条曲线来构建插值函数。Lai和Wenston采用连续三次样条函数计算了椭圆型偏微分方程问题[1]。对于不规则数据点的曲线曲面拟合，通常采用最小二乘法[2]，通过使误差的平方和最小，得到一个线性方程组，求解线性方程组可以得到拟合曲线或者曲面。但是，如果离散数据量比较大、形状复杂，需要分段拟合和平滑处理，实际操作中存在一定的困难。为了克服以上困难，文献[3]利用插值与逼近相结合的曲面拟合思路，较好地解决原始数据点分布不均匀的曲面造型问题。移动最小二乘法对最小二乘法作了改进，能够生成精度高﹑光滑性好的曲线曲面[4-5]。自然邻近插值法是一种较新的插值理论，主要用于多变量不规则数据点的插值。由于Voronoi图和对偶的 Delaunay三角化能够自动调整数据点分布不规则和密度不均匀在空间上的差异，即使对于散乱数据点，也可以得到较好的曲面拟合结果。另外，自然邻近插值法具有严格的插值特性，偏微分方程Garlerkin法可以直接施加本质边界条件，这是移动最小二乘法所无法相比的。Tily和Brace以汽车发动机半规则实验数据为研究对象，对C0连续Sibson插值函数和MATLAB interp2 插值函数进行了比较，发现当实验数据标准化处理后，Sibson 插值函数具有更高的插值精度[6]。高阶偏微分方程的数值计算要求插值函数至少 C1连续，对 C1连续插值函数的插值性能进行深入研究是有必要的。Farin将C0连续Sibson插值函数以自然邻近坐标的形式代入三次单纯形Bernstein-Bézier曲面多项式，构造出C1连续插值函数[7]。Sukumar和Moran提出了一种新的计算方法，将Bernstein基函数转换为C1形函数，保证任意结点I的3个形函数分别与它的3个自由度、和直接相联，从而适合于高阶偏微分方程 Galerkin法[8]。与Sibson插值比较，non-Sibsonian插值具有计算简单、计算效率高等优点[9]，所以本文将non-Sibsonian 插值函数作为三次单纯形Bernstein-Bézier曲面多项式的基坐标，采用文献[8]的计算方法，构造出新的连续自然邻近插值函数，该函数具有二次完备性、对结点函数值和梯度值的插值特性以及在分析域的边界退化为三次多项式等性质。为了考察新建连续插值函数的插值精度及其影响因素，作者将它应用到曲面拟合场合。

1 C1自然邻近插值

1.1 non-Sibsonian自然邻近插值

Voronoi 图及其对偶的Delaunay三角化源自计算几何，是由一组不规则的点定义的最基本的几何结构。考虑平面上由m个离散结点组成的集合，结点I的Voronoi图是指与结点I对应的区域，内任意点到结点I的距离都小于该点到其它结点J的距离，用数学公式表示为

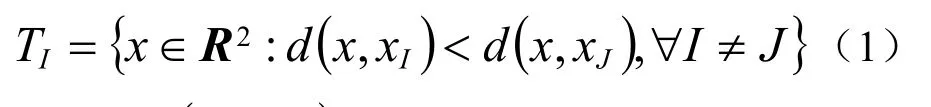
当积分点x被引进集合N的一阶Voronoi 图时，根据空圆准则可以确定点x的自然邻子。图1是平面上7个结点的一阶Voronoi 图，点x共有4个自然邻子，分别是结点1、2、3和4。

假设点x有n个自然邻子，该点关于结点I的non-Sibsonian插值函数可以定义为

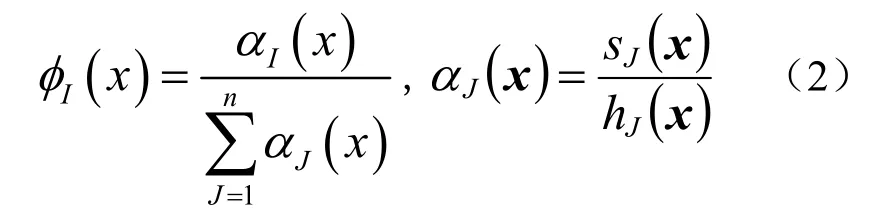
1.2 以non-Sibsonian插值作为自然邻近坐标的C1自然邻近插值函数

将 non-Sibsonian插值φ代入三次单纯形Bernstein-Bézier曲面多项式，沿用文献[8]的计算方法，构造出C1自然邻近插值函数

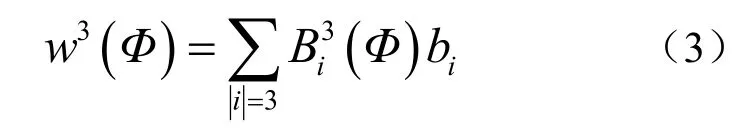
对公式（3）作如下变换，得到

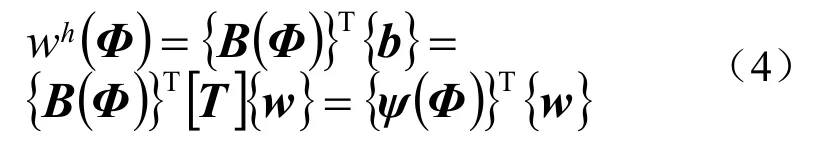
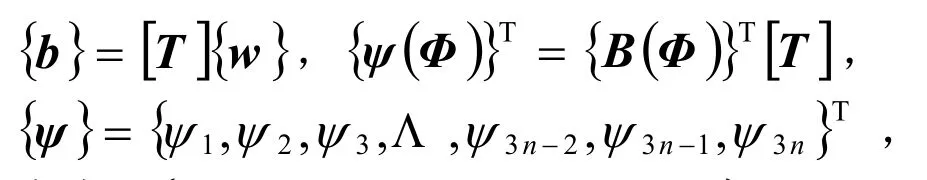
1.2.1 Bernstein-Bézier基函数

non-Sibsonian坐标φ下由积分点x的n个自然邻子组成的n边形的三次基函数为

对于三次Bernstein-Bézier曲面，基函数的多指标记法只会出现下面3种情况：和。表示数组中只有第α个元素为1，其余为0的多指标记法。

1.2.2 变换矩阵的构建

通常，可以把Bézier空间坐标分为顶点、切面和中心Bézier空间坐标三种。三种Bézier空间坐标与结点函数值和梯度值具有不同的构造关系：顶点Bézier空间坐标等于结点函数值，即

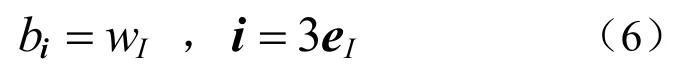
切面Bézier空间坐标为

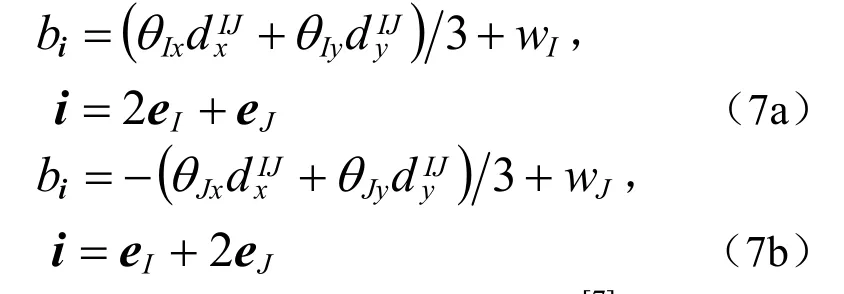
中心Bézier空间坐标的最佳方案为[7]

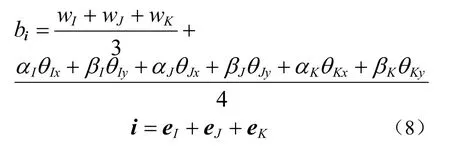
式中

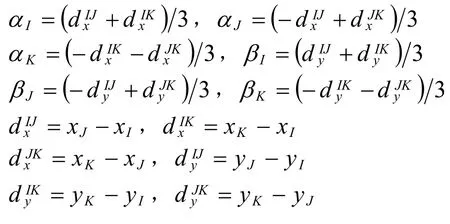
由公式（4）可以看出：变换矩阵的作用是把结点函数值或者梯度值映射到Bézier空间坐标上。利用公式（6）～（8），可以构建出变换矩阵。一旦变换矩阵构建完毕，Bernstein-Bézier基函数和变换矩阵相乘，可以得到形函数

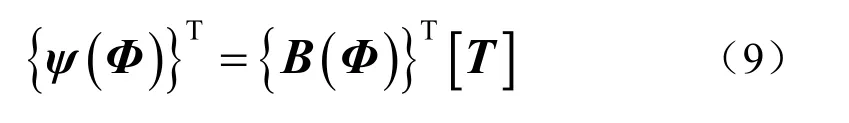
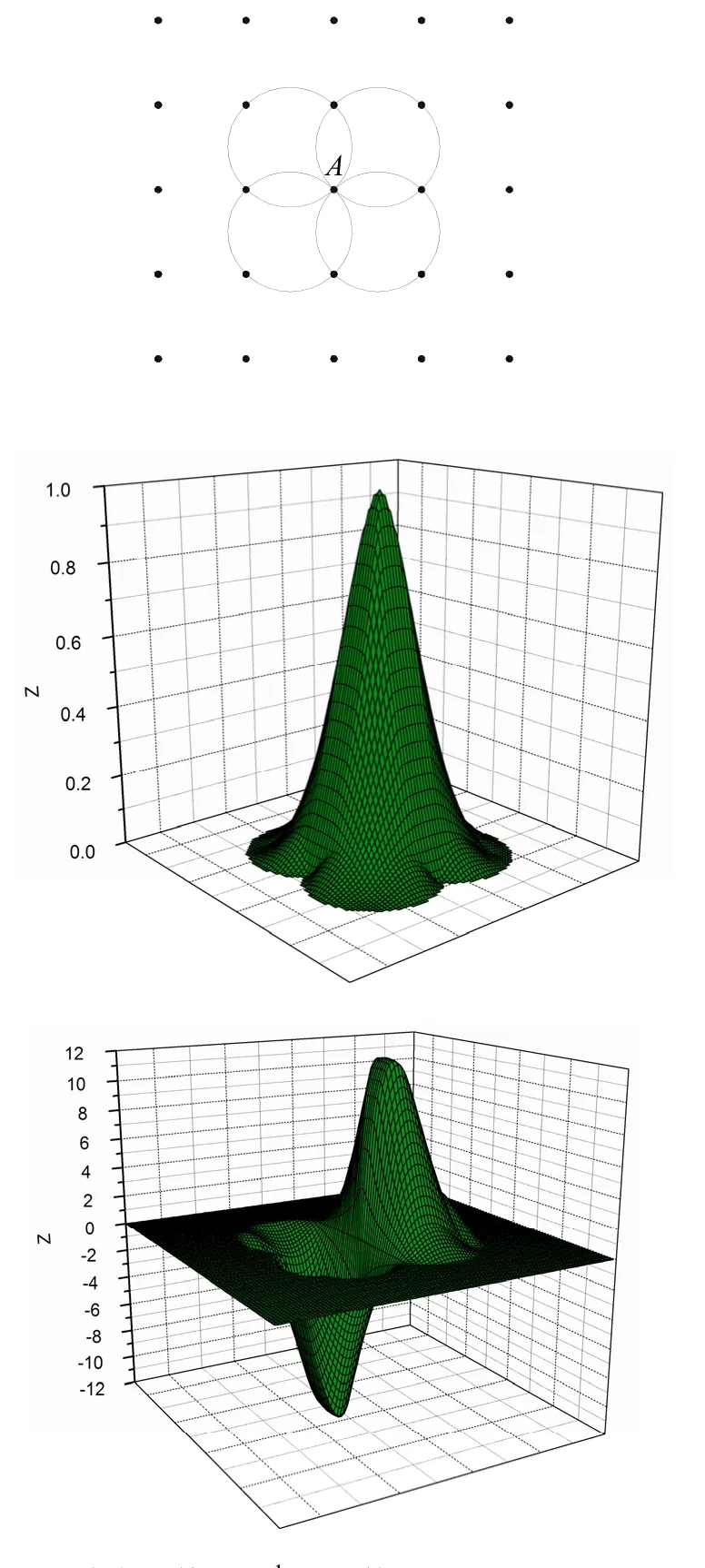
图3 结点网格及?形函数ψ3A-2(x)、ψ3A-1(x)

（1） 高阶连续性

（2） 二次完备性

式中 a为切面Bézier空间坐标的质心，

c为顶点Bézier空间坐标的质心。

（3） 对结点函数值和结点梯度值的插值特性

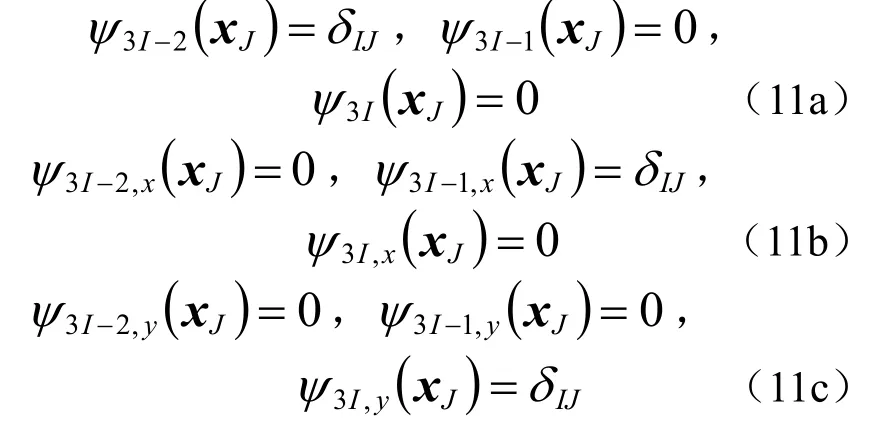
（4） 分析域边界积分点的插值函数是三次多项式

如果点x的两个自然邻子的 non-Sibsonian坐标为，把它们代入方程（12），可以得到

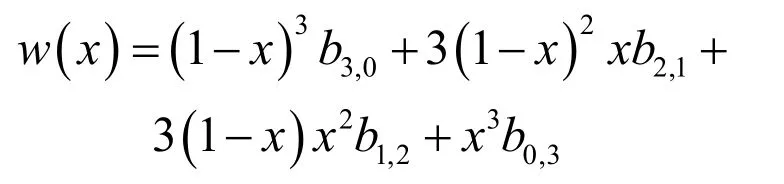
显然，分析域边界上的插值函数是三次多项式。

2 曲面拟合

3个曲面函数分别定义为

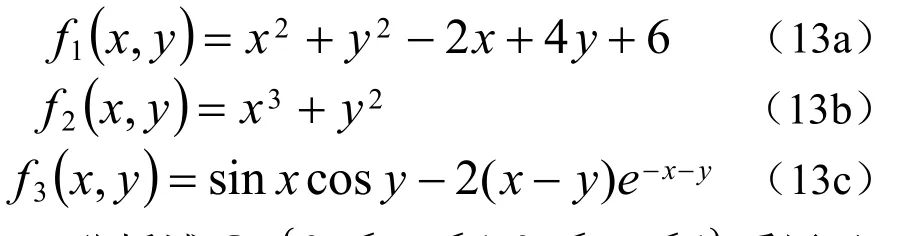
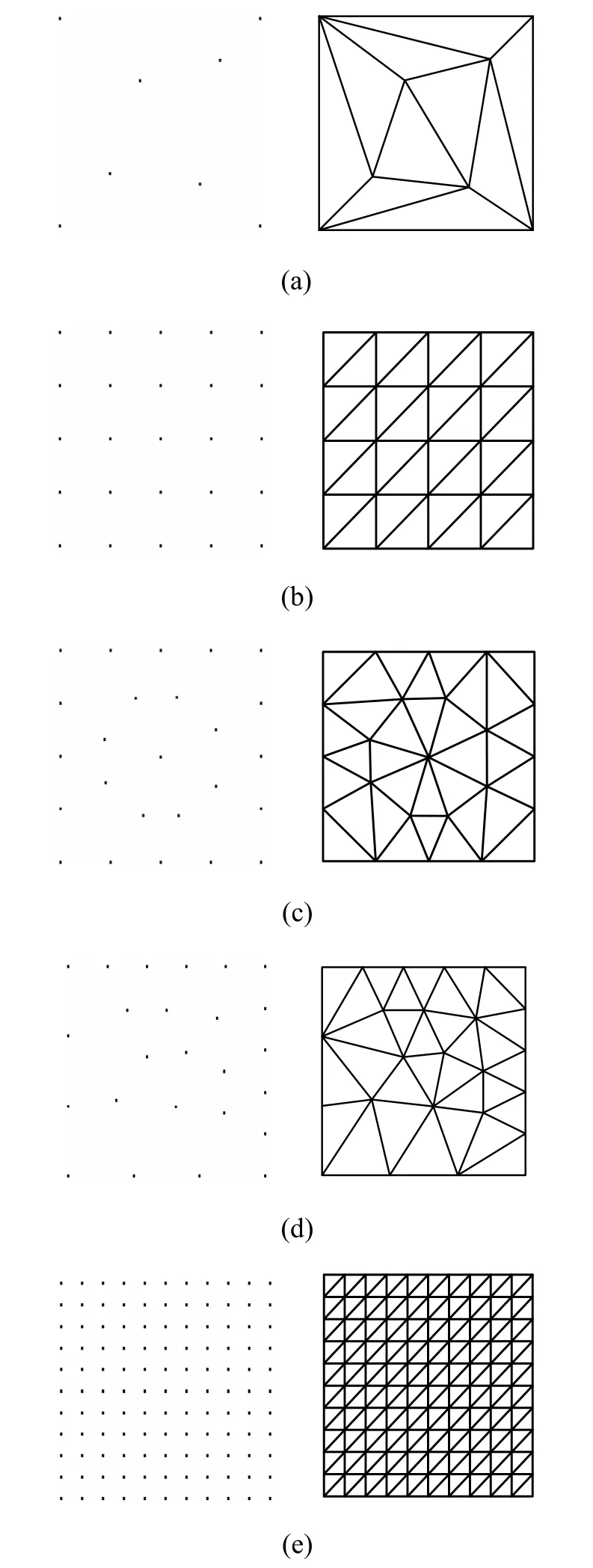
图4 单位正方形离散方案

为了衡量曲面拟合质量，定义整体域Ω的相对误差范Le

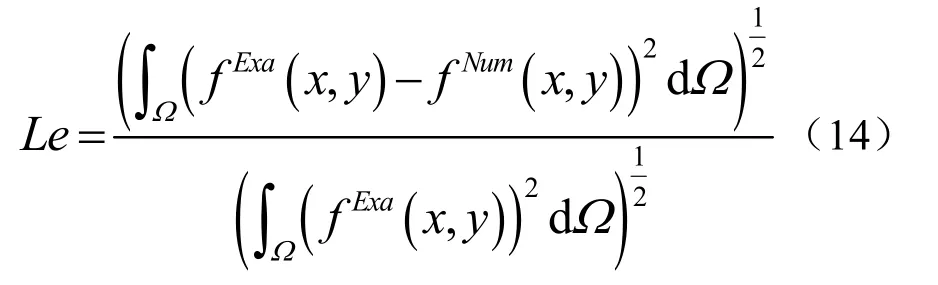
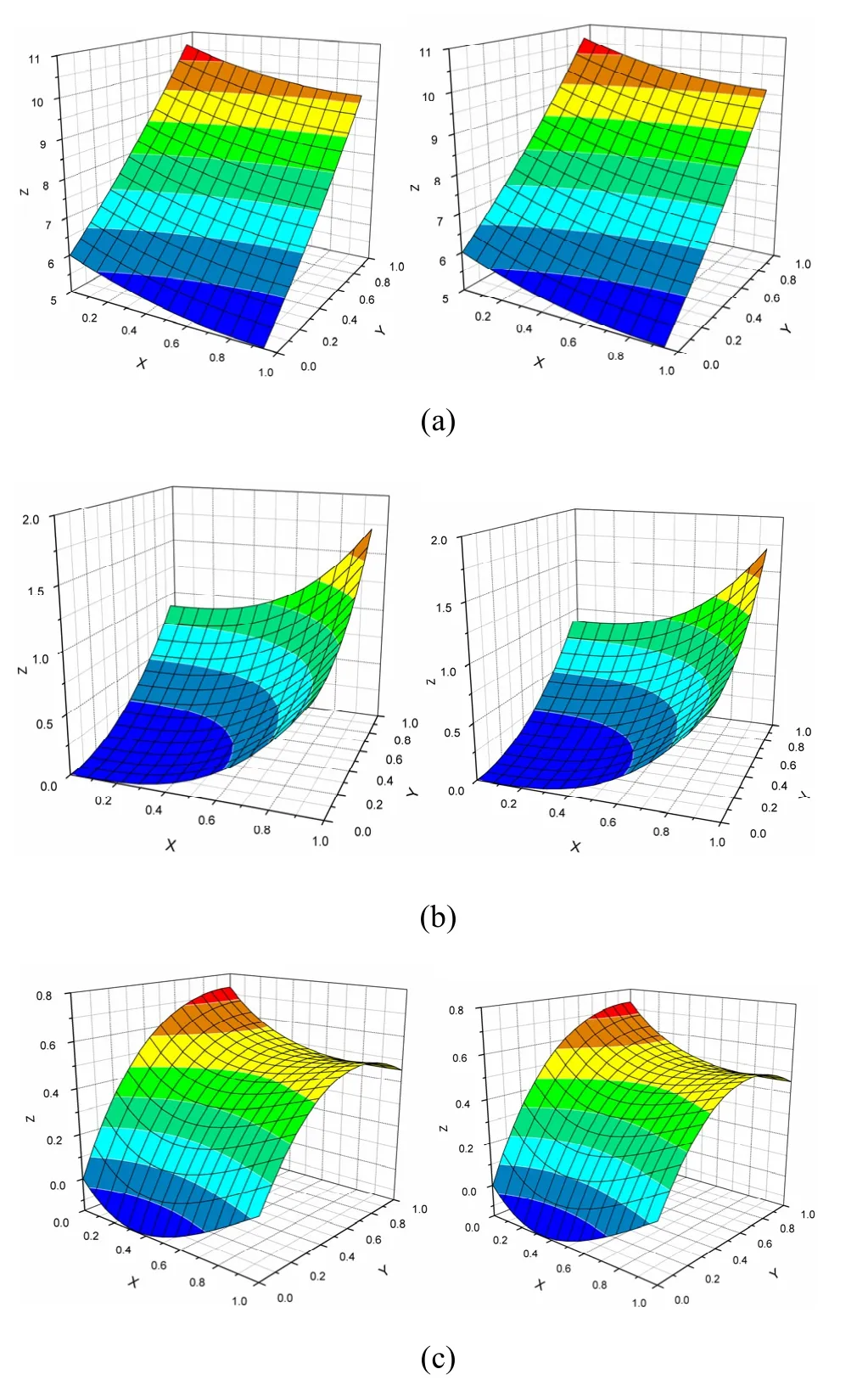
图5 规则25结点的3个函数曲面与拟合曲面的对比（左为函数曲面，右为拟合曲面）

Le值越小，曲面拟合结果越好。3个函数在5种离散方案下的相对误差范Le，见表1。

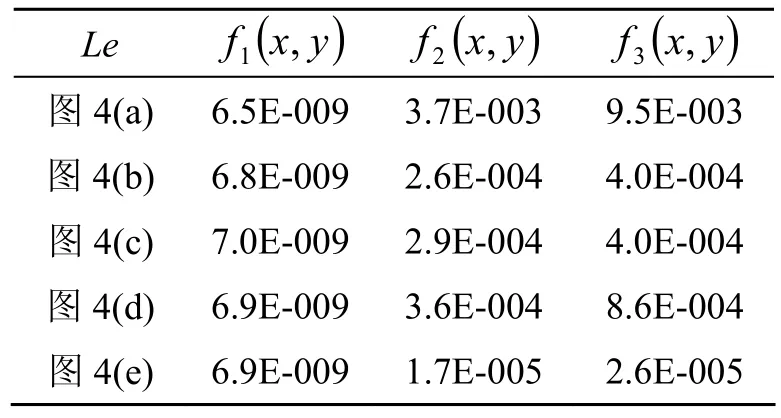
表1 曲面拟合相对误差范Le

3 结 论

（2） 对于高次多项式函数（大于等于3次），曲面拟合质量下降了。离散结点数量对曲面拟合质量影响较大，加密结点可以提高连续插值函数的插值精度，得到质量较高的拟合曲面。由于Voronoi图能够自动调整数据点分布不规则和密度不均匀在空间上的差异，所以对于不规则和密度不均匀数据点的情况，也得到了较好的曲面拟合结果。

[1] Lai M J, Wenston P. Report on numerical experi-ments with bivariate C1cubic splines for numerical solution of partial differential equations [R]. Technical Report, Department of Mathematics, University of Georgia, 1998.

[2] 彭芳瑜, 周 济, 周艳红, 等. 基于最小二乘法的曲面生成算法研究[J]. 工程图学学报, 1999, 20(3): 41-46.

[3] 彭芳瑜, 周云飞, 周 济. 基于插值与逼近的复杂曲面拟合[J]. 工程图学学报, 2002, 23(4): 87-96.

[4] 曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合[J]. 工程图学学报, 2004, 25(1): 84-89.

[5] Lancaster P, Salkauskas K K. Surfaces generated by moving least squares methods [J]. Mathematics of Computation, 1981, (37): 141-158.

[6] Tily R, Brace C J. A study of natural neighbour interpolation and its application to automotive engine test data [J]. Proceeding of I mech E, Part D: Journal of Automobile Engineering, 2006, (220): 1003-1017.

[7] Farin G. Surfaces over Dirichlet tessellations [J]. Computer Aided Geometric Design, 1990, (7): 281-292.

[8] Sukumar N, Moran B.natural neighbor interpo-lant for partial differential equations [J]. Numerical Methods for Partial Differential Equations, 1999, 15(4): 417-447.

[9] Sukumar N, Moran B, Semenov A Y, et al. Natural neighbor Galerkin methods [J]. International Journal for Numerical Methods in Engineering, 2001, (50): 1-27.

Surface Fitting Based on C1Natural Neighbor Interpolation

NIE Zhi-feng1,2, ZHOU Shen-jie1, WANG Kai1, KONG Sheng-li1
( 1. School of Mechanical Engineering, Shandong University, Jinan Shandong 250061, China; 2. College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao Shandong 265510, China)

C1natural neighbor interpolation can be realized when C0non-Sibsonian interpolation is introduced in the Bernstein-Bézier surface representation of a cubic simplex. The principle and properties of C1natural neighbor interpolation are described and the surface fitting is given. The Voronoi diagram can adjust the spatial discrepancy caused by irregular data and data of varying density, so even for the scattered data, C1natural neighbor interpolation can get accurate fitting results.

computer application; surface fitting; C1natural neighbor interpolation; Bernstein-Bézier polynomial

TP 391

A

：1003-0158(2010)01-0110-06

2008-08-01

国家自然科学基金资助项目（10572077）；山东省自然科学基金资助项目（Y2007F20）；山东科技大学“春蕾计划”资助项目（2009AZZ021）

聂志峰（1970-），男，山东日照人，博士研究生，主要研究方向为数值计算方法。