基于有向图的二维约束求解算法研究

王世平， 郭连水

（北京航空航天大学机械工程及自动化学院，北京 100191）

基于有向图的二维约束求解算法研究

王世平， 郭连水

（北京航空航天大学机械工程及自动化学院，北京 100191）

针对过约束、几何完全定义状态判定和约束求解效率等问题，提出了基于约束图，利用自由度理论和约束冲突机制，通过反向约束方向平衡约束，进而通过排序进行约束求解的算法。算法采用约束图记录约束和几何的关系；通过约束平衡的方法进行过约束和几何完全定义的判定；采用排序求解方法，将庞大计算问题转化为一组相对简单的计算问题。算法已得到初步应用，对过约束和几何完全定义状态的判定有明显的效果，而且提高了约束求解效率。

计算机应用；几何约束求解；约束图；过约束；完全定义；排序求解

约束求解是CAD变量化系统草图设计的重要组成部分，用以满足快速交互设计的需要。国内外学者进行了大量的研究，主要方法有基于数值求解、基于符号求解、基于规则求解和基于图论求解[1]。其中基于图论的求解方法[2-6]最为直观、严谨，而且可以方便地进行过约束和几何完全定义状态的判断。

J Y Lee和K Kim提出的全约束下的图论和数值相结合的方法[1]是目前应用最广泛的方法之一。赵万生等提出的局部影响域算法[3]给出了一种应用图论解决欠约束问题的方法。董金祥等提出的基于图论的拓扑排序方法[4]不但适用于欠约束情况，而且也能处理较简单的过约束问题。目前的文献对简单的过约束问题（剩余自由度小于零）有一定的探讨，但对于相对复杂的过约束和对几何完全定义状态的确定却少有涉及。

本文从变量化造型系统应用出发，重点讨论约束信息的管理、过约束和几何完全定义状态的判定、排序求解方法等，建立了二维约束求解算法：记录约束图约束和几何的关系，作为约束求解的基础；调整约束图平衡约束，判定过约束和几何完全定义状态；以调整后的约束图为基础，将需要计算的几何元素进行排序，高效完成方程组求解。

1 约束模型表示方法

在进行复杂草图设计时，常常面临约束关系管理的问题。本文采用约束图表达约束模型，图的顶点表示几何元素，边表示约束。约束图将相互关联的所有几何和约束联系在一起。

1.1 顶点

顶点 表示某一几何元素，如点、直线、圆等。

顶点分为前承顶点和传递顶点两种。两类顶点是相对于约束边来区分的。如图1(a)，约束e1箭头指向的顶点L1称为e1的传递顶点，约束e1箭头起始的顶点P1称为e1的前承顶点。

1.2 约束边

约束边 用带箭头的约束边（有方向的边）来表示某一约束。

约束边分为前承约束和传递约束两种。两类约束是相对顶点来区分的。如图1(a)，指向顶点L1的约束边e1称为L1的前承约束，从顶点L1起始的约束边e2称为L1的传递约束。

1.3 约束图建立方法

约束图 由顶点和约束边组成的图形，称为约束图。

约束图的建立过程就是创建新的顶点和约束边，并将它们联系在一起的过程。

示例如图1所示。

建立由3个点P1、P2、P3和3条直线L1、L2、L3组成的三角形，如图1(a)所示。在约束图中创建6个几何元素的顶点P1、P2、P3、L1、L2、L3；之后创建6个点在直线上的约束e1～e6；建立这6条约束边与顶点之间的关系：e1是P1与L1之间的约束（e1由P1指向L1），e2～e6类似处理，如图1(b)所示。

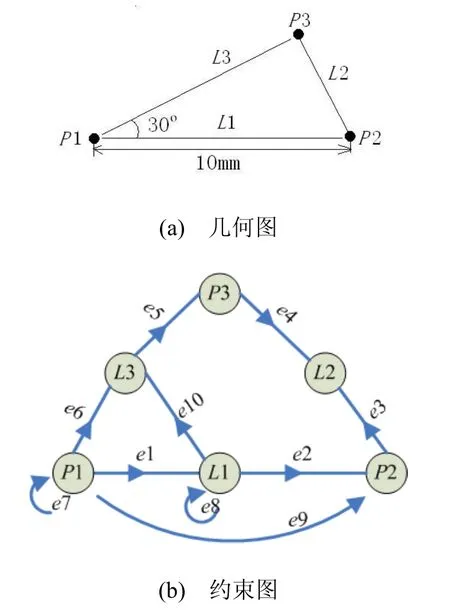
图1 几何图和约束图

新添加两点P1与P2间10mm的距离约束e9。首先在约束图中创建约束边e9，之后建立约束边e9与顶点P1与P2的关系（e9由P1指向P2）。新添加点P1的固定约束e7、直线L1的水平约束e8、两直线L1与L3间的30º角度约束e10。

约束是有向的。不同的约束方向表示不同的约束方式和计算方式。如图 1(b)，距离约束 e9是由P1指向P2的，这表示点P1通过10mm的距离来约束点P2；在计算P2时，可以通过P1的位置和10mm的距离约束e9来求解P2的位置。

在约束图的建立过程中，约束方向的确定将影响约束求解过程。本文是先任意选取一个方向，再通过下文约束平衡方法来修改约束的方向，避免因约束方向不当而引起几何的过定义。

2 基于约束图的约束平衡方法

通过约束图的调整（修改约束的方向）平衡约束关系，无法平衡的约束则为过约束。在约束求解方程组计算之前平衡约束关系，能够避免几何过定义导致的无解方程组计算，提高求解效率。

2.1 过约束的概念

几何过定义 由于几何的约束冗余导致约束求解失败，称其为几何过定义。

过约束 导致约束图存在过定义几何的约束称为过约束。

导致几何过定义的原因主要有 2个：① 几何的剩余自由度小于零；② 约束冲突。前者是由于约束过多，后者是由于约束彼此相矛盾造成了几何的无解。

剩余自由度 某几何的自由度减去其前承约束的约束度之和，其差值称为该几何的剩余自由度。

RDOF(P)= DOF(P)-∑DOC(ei) （1）例如，如图 1中，直线 L1的剩余自由度RDOF(L1)= DOF(L1)-∑DOC(ei)=2-1-1=0。

约束冲突 多个约束相互矛盾而导致约束求解失败，称其为约束冲突。

约束冲突举例：如图1(b)约束图，若反向角度约束e10，则角度约束e10与水平约束e8产生约束冲突。在计算直线 L1时，其方向或水平，或与L3成30°角，二者选其一。约束e10与e8彼此矛盾，不能同时指向同一个几何。

2.2 约束平衡方法

从几何过定义的概念知道，过定义的出现实际上是由于几何的约束负担（前承约束）过重。为了避免几何过定义，需要进行约束平衡，即减少过定义顶点的前承约束。

修改约束方向后，该约束新指向的几何有可能会由原来的非过定义状态转变为过定义状态。那么，如何选择合适的前承约束进行反向以及反向约束后产生新的过定义几何时的处理方法就成为算法的关键。算法主要步骤如下：

Step 1 找到过定义顶点P0（剩余自由度小于0的顶点或相冲突的约束的传递顶点）。

Step 2 在P0的前承约束中挑选一个约束e进行反向，要求反向e后P0不再是过定义顶点。反向约束e后进入下一步Step 3。若没有合适的前承约束可以反向，分下列两种情况：若P0是因为反向约束 e0导致的过定义顶点，那么恢复e0的方向，重新选择一个合适的前承约束反向（即返回上一个访问顶点转Step 2）。若P0是最初的那个过定义顶点，那么，算法结束，该约束图存在过约束，约束平衡失败。

Step 3 被反向的约束e的传递顶点P1，若P1不是过定义顶点，则约束图调整成功（约束平衡成功），约束图不存在过约束；若P1是过定义顶点，将P1当作P0，转Step 2。

示例 在图1(a)几何图中，新添加L2与L1的垂直约束 e11，如图 2(a)。过定义顶点可能是新添加约束e11的传递顶点L1。

如图 2(a)，L1是过定义顶点，其前承约束e11和e8约束冲突，且L1的剩余自由度小于0。由于存在约束冲突，只能反向e8或e11（反向其他前承约束无法解除L1的过定义状态）。反向e8后L1仍是过定义状态，恢复e8的方向（反向e8失败）；反向约束e11，使L1不再是过定义顶点，如图2(b)所示。

反向e11后，e11的传递顶点L2变为过定义顶点，其剩余自由度小于0。反向L2的前承约束e3，使L2不再是过定义顶点，如图2(c)所示。

反向e3后，e3的传递顶点P2变为过定义顶点，其剩余自由度小于 0。反向 P2的前承约束e9，使P2不再是过定义顶点，如图2(d)所示。

反向e9后，e9的传递顶点P1变为过定义顶点。P1没有合适的前承约束可以反向，恢复 e9的方向，如图2(c)所示。

重新选择P2的一个前承约束e2进行反向，使P2不再是过定义顶点，如图2(e)所示。按照之前的分析方法可得反向e2失败，恢复e2的方向，如图2(c)所示。

P2没有合适的前承约束可以反向，恢复e3的方向，如图2(b)所示。

重新选择L2的一个前承约束e4进行反向，使L2不再是过定义顶点，如图2(f)所示。

反向e4后，e4的传递顶点P3不是过定义顶点，约束图调整成功（约束平衡成功）。

由上例可以看出，约束平衡是由新添加或修改的约束为起始的。实际上，每次添加或修改新的约束时，都要进行约束平衡。如此，下次新添加或修改约束就是在平衡约束图基础上的操作，只需要考虑新的约束带来的影响即可。

图2 约束平衡方法示意图

2.3 过约束判断

过约束判断问题不仅需要判断出过约束是否存在，还要判断出过约束的几何对象和过约束的位置。过约束判断规则如下：

规则1 约束平衡失败，则存在过约束；否则不存在过约束。

规则2 约束平衡失败后，约束图中所有反向失败的约束都是过约束。

规则3 过约束指向的几何就是过约束所在的几何。

由于约束冲突的判断机制，上述规则可以判断出许多特殊的过约束。

示例 如图3的几何图和约束图，e1～e4是点在直线上约束；e5是直线L1的水平约束；e6是直线L2的竖直约束；e7是圆C1与直线L2的相切约束。新添加L1和L2的平行约束e8。按照算法进行约束平衡，如图3(b)，结果是约束平衡失败，判定约束图存在过约束；约束图中e5、e6和 e8反向失败（由于约束冲突的机制，其他约束没有被反向），判定为过约束；它们所指向的几何L1和L2为过约束所在几何。即水平、竖直和平行约束为过约束，直线L1和L2为过约束所在的几何。（而相切约束等则不是过约束，圆等也不是过约束所在几何。）

图3 过约束判断示意图

2.4 几何完全定义状态分析方法

几何完全定义状态的判定有利于提高系统的交互设计。设计者可以参考现有几何的约束状态进行下一步的设计，避免过约束的出现。

完全定义状态 几何的形状和位置完全确定时的状态称为完全定义状态。

几何的完全定义状态判断规则如下：

规则1 该几何的前承约束中不存在过约束。

规则2 几何的剩余自由度等于0。

规则3 在约束图中，反向该几何的任意一个前承约束，利用约束平衡方法，结果是反向失败，即该几何的所有前承约束均无法反向。

满足以上所有条件的几何，处于完全定义状态。

示例 如图4，点P1有固定约束e1，点P1与直线 L1间存在点在直线上约束 e2，直线 L2有水平约束e3，直线L1和L2之间存在平行约束e4。用上述规则进行完全定义状态的判断：

P1的前承约束e1不是过约束，P1剩余自由度为0，e1不能反向，因此P1是完全定义状态。

L1的前承约束e2、e4不是过约束，L1的剩余自由度为0，反向e2和e4均失败（e3和e4互为约束冲突，同时指向L2时出现过定义），因此L1是完全定义状态。

L2的前承约束e3不是过约束，但L2的剩余自由度为1，因此L2不是完全定义状态，而处于欠定义状态。

需要注意的是，“只有前承几何完全定义，其传递几何才可能完全定义”的观点是错误的。如图4，L1的前承几何是L2，即L1是根据L2计算出来的，而L2不是完全定义状态，L1却是完全定义状态。

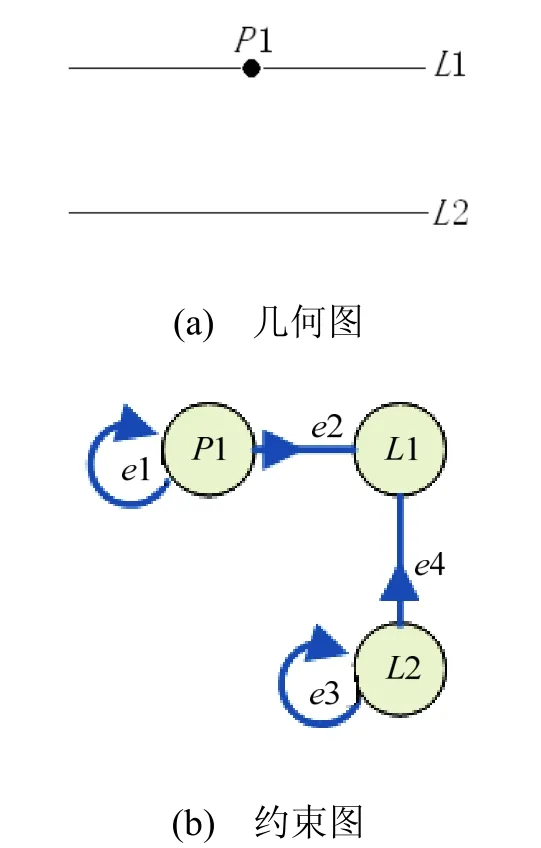
图4 完全定义状态判断示意图

3 基于约束图的约束求解队列算法

根据调整（约束平衡）后的约束图，进行求解排序，对需要求解的几何按排序结果进行方程组的顺序求解。

3.1 基本思路

在新添加或修改约束时，求解前的几何图形满足除了新约束外的所有约束，所以，只需要以新约束作为起始 ，计算新约束影响到的几何 P以及因为几何P的改变而影响到的其他几何。至于未影响到的几何，作为已知几何，不重新计算。

在重新计算几何过程中，如果所有需要计算的几何同时求解，计算量将会非常大。（等价于n元m次方程组。）如果将求解的几何进行排序，按照顺序依次求解几何，那么计算量将会大大减少。（等价于将一个大方程组拆分为若干小方程组，降低了方程组的元数。）

3.2 求解队列算法

求解队列算法的基本思路是：以新添加或新修改约束的传递顶点为起始点，沿着传递约束的方向，将几何排序。排序后得到的有序队列，就是需要重新计算的几何元素的求解队列。求解队列中的每个队列元素含有一个或多个几何元素，同一个求解队列元素内的几何元素在计算中同时求得。算法如下：

Step 1 将求解队列Queue清空；

Step 2 得到新添加或新修改约束 e的传递顶点P0；

Setp 3 将 P0作为一个求解队列元素压入求解队列Queue的队尾；

Step 4 遍历P0的传递约束。若P0的传递约束都遍历完毕，则转Step 9。否则，选中一条未遍历的传递约束e1，得到e1的传递顶点P1；

Step 5 若P1不在求解队列Queue中，则记录P1的父顶点：F（P1）＜—P0，将P1当作新的P0：P0＜—P1，转Step 3。若P1在求解队列中，得到P0的父顶点，记为P2，清空临时堆栈tempStack，将P0压入tempStack；

Step 6 将P2压入临时堆栈tempStack。若顶点P2就是顶点P1，或P2、P1属于同一个求解队列元素，（说明求解队列中从P1到P0的顶点构成了环路），则转Step7。否则，将P2的父顶点当作新的P2：P2＜—F（P2），转Step 6。若顶点P2没有父顶点（即P2是起始点），转Step 8；

Step 7 调整求解队列，将临时堆栈tempStack内所有顶点所在的队列元素合并为一个，将新的队列元素置于求解队列中P1所在队列元素的位置，转Step 4；

Step 8 若求解队列中，P1所在队列元素在P0所在队列元素之后，转Step 4。否则，调整求解队列，将P1所在队列元素以及沿着P1传递约束方向遍历到的所有顶点所在的队列元素置于P0所在队列元素之后，转Step 4；

Step 9 若P0没有父顶点（即P0是起始点），则算法至此结束。若P0有父顶点，则返回P0的父顶点，即将P0的父顶点当作新的P0：P0＜-F（P0），转Step 4。

示例 在图 2约束平衡后执行求解队列算法，如图5(b)所示。

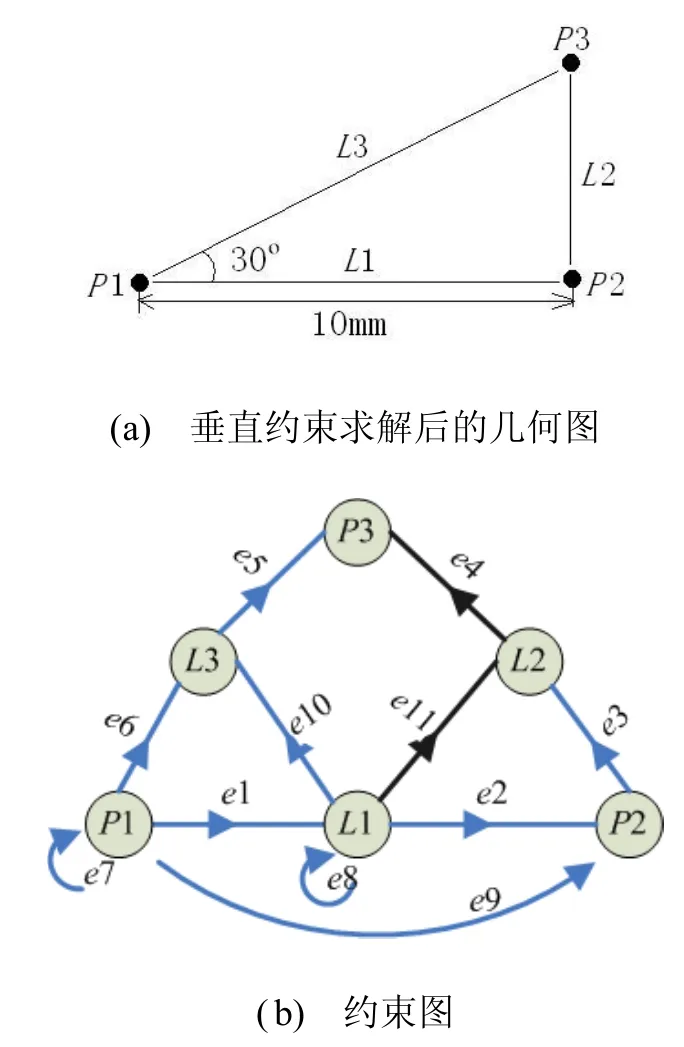
图5 添加垂直约束后的几何求解

将新添加垂直约束e11的传递顶点L2压入求解队列，求解队列变为：L2。遍历L2的传递约束e4，得其传递顶点P3，P3不在求解队列中，将P3压入求解队列中，求解队列变为L2—＞P3。P3没有传递约束，返回到P3的父顶点L2。L2的传递约束遍历完毕，又L2是起始点，算法结束。最终得到求解队列：L2—＞P3，即先通过几何L1、P2和约束e11、e3计算L2，再通过几何L2、L3和约束e4、e5计算P3。最终得到的图形就是一张满足所有约束的正确图形。约束求解后的几何如图5中的几何图。

4 结 论

本文提出的约束求解算法概括为：以约束图为基础，通过调整约束图平衡约束，通过求解队列算法，提高求解速度，实现约束求解。该算法已经初步应用于变量化造型系统中，经实例验证（如图6），可完成约束高效求解，效果良好。结论如下：

图6 实例验证

（1） 约束图模型解决了复杂约束信息的管理问题。通过约束图，将几何元素和约束有机的联系在一起。

（2） 通过约束图的调整来平衡约束，进行过约束的判定，可以避免某几何过定义导致的无解方程组计算；进行几何的完全定义状态的判定，可以为设计者的设计工作提供依据，提高人机交互设计的效率。

（3） 求解队列算法可以在添加或改变约束时给出需要计算的几何以及几何的计算顺序，将复杂约束图进行分解，“分而治之”，提高求解效率。

[1] Lee J Y, Kim K. A 2-D geometric constraint solver using DOF based graph reduction [J]. Computer Aided Design, 1998, 30(11): 883-896.

[2] Bouma W, Fudos I, Hoffmann C, et al. A geometric constraint solver [J]. Computer Aided Design, 1995, 27(6): 487-501.

[3] 赵万生, 王 刚, 姜洪臣, 等. 二维欠约束系统求解算法的研究[J]. 哈尔滨工业大学学报, 2002, 34(1): 54-57.

[4] 董金祥, 葛建新, 高 屹, 等. 变参绘图系统中约束求解的新思路[J]. 计算机辅助设计与图形学学报, 1997, 9(6): 513-519.

[5] 蒋丹东, 何援军, 杨 东, 等. 基于点簇归约的几何约束求解器研究[J]. 高技术通讯, 2002, (6): 49-53.

[6] 罗 浩, 陈立平, 周 济. 基于归约的几何约束推理研究[J]. 计算机辅助设计与图形学学报, 1997, 9(3): 256-262.

2D Geometric Constraint Solving with Directed Graph

WANG Shi-ping, GUO Lian-shui
( School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

In order to solve the over-constrained problem and enhance computational efficiency, an algorithm, which is based on the constructing directed constraint graph, revealing constraint conflict, then reversing the direction of the related constraint to balance the constraint graph, and finally sorting the graph to get the solving sequence of geometric entities, is presented. The method of balancing constraints can help transforming the over-constrained problem into well-constrained.

computer application; solution of geometric constraint; constraint graph; over-constrained; well-constrained; sort algorithm

TP 391

A

：1003-0158(2010)01-0054-07

2008-07-17

王世平（1983-），男，山东昌邑人，硕士研究生，主要研究方向为几何造型技术。