基于一元对称幂基的等距曲面有理逼近算法

张 莉， 檀结庆， 刘 植

（1. 合肥工业大学计算机学院，安徽 合肥 230009；2. 合肥工业大学数学系，安徽 合肥 230009）

基于一元对称幂基的等距曲面有理逼近算法

张 莉1,2， 檀结庆1,2， 刘 植1,2

（1. 合肥工业大学计算机学院，安徽 合肥 230009；2. 合肥工业大学数学系，安徽 合肥 230009）

给出了基于一元对称幂基的等距曲面蒙面逼近新算法。利用一元对称幂基逼近张量积Bézier曲面u向曲线的等距曲线，得到一组等距逼近曲线，取固定的v值，得到一组数据点，用反算控制顶点的方法得到过这组数据点的v向曲线。对这两组曲线用蒙面算法得到逼近的有理等距曲面。该算法计算简单，将二元等距曲面有理逼近转化为一元曲线有理逼近，同时方便地解决了整体误差问题，随着对称幂基阶数的升高，可以得到较理想的逼近效果。

计算机应用；等距曲面；张量积Bézier曲面；对称幂基；有理逼近；蒙面算法

随着机器人、数控机床以及带厚度薄片实体（如汽车车身、箱包等）在计算机图形学和数控加工中的大量应用，等距曲线/曲面(offset)的研究已经成为近些年来 CAGD（计算机辅助几何设计）的研究热点。关于平面曲线的等距曲线已有大量的研究[1-5]，但对等距曲面的研究工作则相对较少[6-7]。

对于简单曲面的等距曲面的生成，国内外许多学者做了大量的工作：Farouki[8]指出三类简单实体：凸多面体、旋转体和拉伸体具有精确的等距曲面。Pottmann[9]在1995年提出了PH 曲面的概念，即具有有理等距曲面的一类曲面。吕伟[10]证明了抛物面、椭球面和双曲面的等距曲面仍为有理曲面。接着 Pottmann 等[11]证明了不可展有理直纹面的等距曲面在整个空间是可有理化的。然而对于更为复杂的曲面生成其等距曲面却颇为困难。2000年刘利刚、王国瑾[12]把等距曲面的问题看作球心在原曲面上运动，半径为d的基球面沿原曲面扫掠的问题，用三角网格来逼近基球面得到了基于球面三角网格逼近的等距曲面逼近算法。

本文利用一元对称幂基逼近张量积 Bézier曲面u向曲线的等距曲线，对得到的一组等距逼近曲线，取固定的v值，得到一组数据点，用反算控制顶点法得到过这组数据点的v向曲线。以u向等距逼近曲线为平面截线，以得到的v向曲线为脊线，最后用过关键位置的蒙面算法得到有理等距曲面，较为巧妙的将二元等距曲面的有理逼近问题转化为一元等距曲线的有理逼近问题，简化了算法，同时方便地解决了整体误差问题。

1 预备知识

1.1 对称幂基函数的定义

Sánchez-Reyes[13]给 出 如 下 对 称 幂 基（Symmetric power basis）的定义：

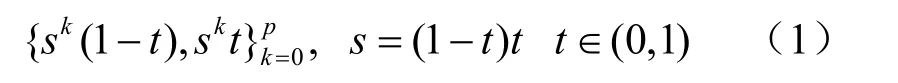
对称幂基函数有以下特点：① 它是对称的，将变量 t用（1-t）替换，得同一组基；② 低阶基函数是高阶基函数的子集；③ 在端点t=0, t=1，直至k-1阶导数为零。因此Sánchez-Reyes称用这种基函数表示的多项式为“Hermite两点展开多项式”，称用对称幂基函数逼近已知函数为“两点Hermite插值逼近”。性质③ 保证了函数在端点t=0, t=1处

也可以简写成

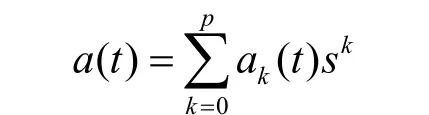
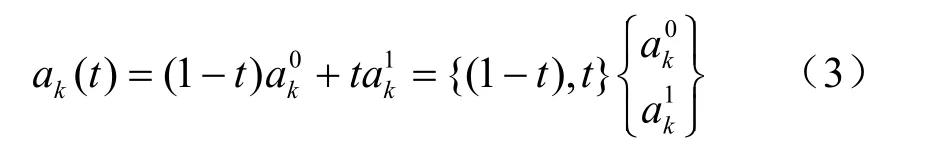
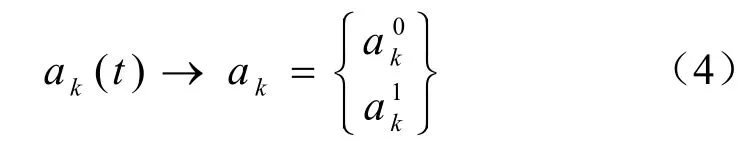
1.2 对称幂基函数的运算

文献[14]给出了对称幂基函数表示的多项式之间的四则运算以及求平方根运算，下面介绍其中的加法、减法及乘法运算。

两个用对称幂基函数表示的多项式函数的加法和减法计算非常简单，就是对应的分量相加或相减，而对用Bernstein基表示的函数，不同阶的两个多项式无法直接相加或相减，必须通过升阶或降阶。

给定两个对称幂基函数表示的m次和n次多项式，它们的系数序列分别为，，下面介绍它们的乘法运算。为了得到用对称幂基函数表示的两个多项式乘法，首先了解它们“系数”是怎样相乘的。两个线性函数分别用Bézier坐标表示

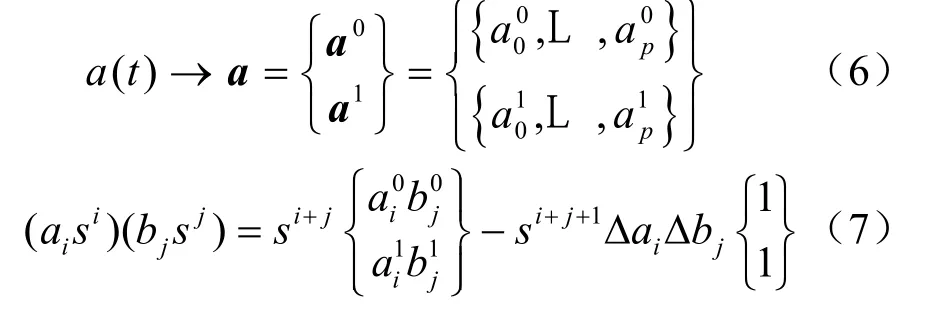
由式（5）、（6）、（7）即得对称幂基表示的多项式的乘法。

1.3 等距曲面的定义

2 张量积Bézier曲面的等距曲面的有理逼近算法和误差估计

2.1 张量积Bézier曲面的u向Bézier曲线的等距逼近

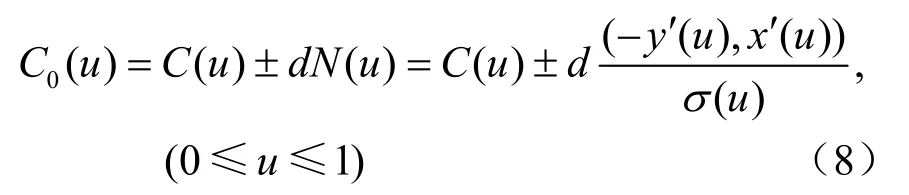
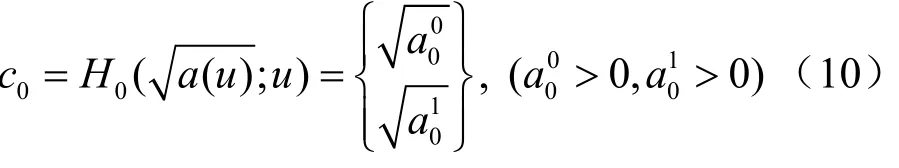
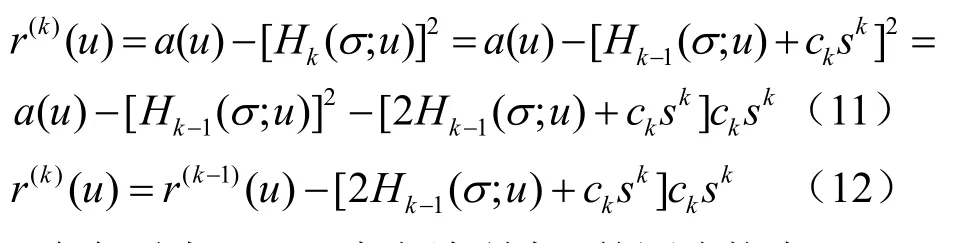
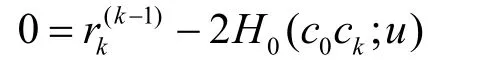
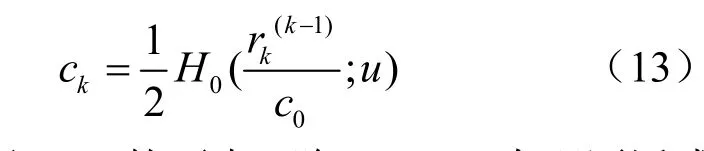
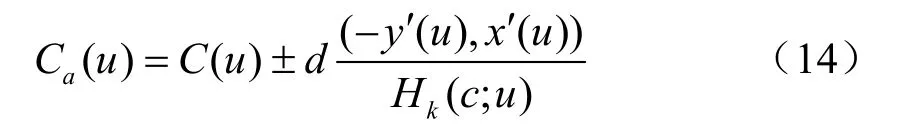
利用对称幂基到Bernstein基的转换公式，式（14）中计算出的逼近等距曲线是用 Bernstein基表示的有理表达式。

图1是三次平面Bézier曲线，控制顶点为：p0=[0,0]; p1=[1,2]; p2=[3,2]; p3=[4,0]。采用上述方法，取等距距离d = 0.5的等距曲线进行有理逼近，其中实线为原曲线及等距曲线，虚线为等距曲线的有理逼近曲线。误差分别为：

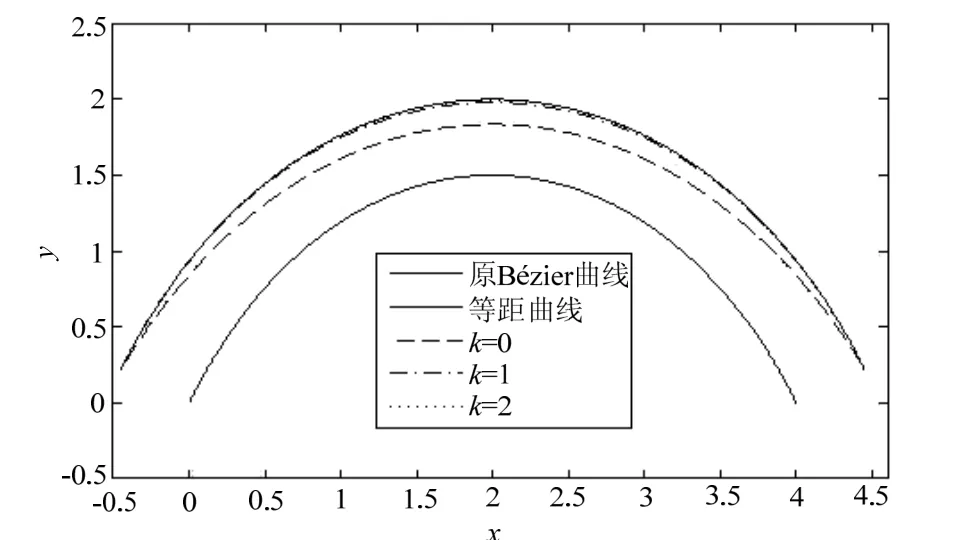
图1 三次平面Bézier曲线等距有理逼近

2.2 张量积Bézier曲面的v向数据点的插值逼近

2.3 带伸缩因子的蒙面算法

文献[15]给出了由截面曲线、脊线以及局部活动标架构造而生成的蒙面曲面

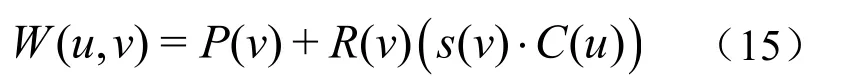
2.4 误差估计

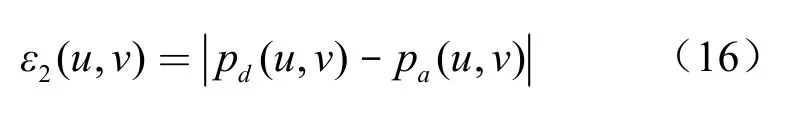
3 数值实例

图2是3×3的张量积Bézier曲面，控制顶点分别为

图3画出了原Bézier曲面和它的精确等距曲面。图4按照本文算法生成的截面曲线和脊曲线（给出了多条）。图5是蒙面后的逼近等距曲面，图6是原Bézier曲面和它的逼近等距曲面，这里u向曲线的等距逼近曲线使用了u的五次多项式逼近。图7是逼近等距曲面的误差曲面。

图 2 原Bézier曲面

图 3 原Bézier曲面和它的精确等距曲面

图 4 本文算法所得的截面曲面曲线和脊曲线

图 5 图3蒙面后的逼近等距曲面（k=2）

图 6 原Bézier曲面和它的逼近等距曲面（k=2）

图 7 逼近等距曲面的误差曲面

4 总结和展望

本文对等距曲面的有理逼近做了一个有益的尝试，将对二元曲面的等距有理逼近转换为对一元曲线的等距有理逼近，结合蒙面算法生成逼近等距曲面，简化了逼近算法。算法优点在于对整张曲面u向曲线变化不大（如有伸缩变化、旋转变化等），做等距曲面有理逼近可以得到较为理想的效果，尤其对工业设计中比较规则的曲面的等距面可以取得很好的效果。对整张曲面而言，若u向曲线变化比较复杂，本算法逼近效果不太理想，需结合其它较为复杂的蒙面算法才能得到理想的逼近曲面。

[1] Klass R. An offset spline approximation for plane cubic splines [J]. Computer Aided Design, 1983, 15(5): 297-299.

[2] Tiller W, Hanson F. Offsets of two dimensional profiles [J]. IEEE Computer Graphics and Its Applications, 1984, 4(9): 36-46.

[3] Hoschek J. Spline approximation of offset curves [J]. Computer Aided Geometric Design, 1988, 5(1): 33-40.

[4] Lee I K , Kim M S, Elber G . Planar curve offset based on circle approximation [J]. Computer Aided Design, 1996, 28(8): 617-630.

[5] Elber G Lee. Comparing offset curve approximation methods [J]. IEEE Computer Graphics and ItsApplications, 1997(5-6): 62-71.

[6] Pham B. Offset curves and surfaces: a brief survey [J]. Computer Aided Design, 1992, 24(4): 223-229.

[7] Maekawa T. An overview of offset curves and surfaces [J]. Computer Aided Design, 1999, 31(3): 165-173.

[8] Farouki R T. Exact offset procedures for simple solids [J]. Computer Aided Geometric Design, 1985, 2(3): 257-279.

[9] Pottmann H. Rational curves and surfaces with rational offsets [J]. Computer Aided Geometric Design. 1995, 12(2): 175-192.

[10] Lü W, Wien. Rational parameterization of quadrics and their offsets [J]. Computing, 1996, 57(2): 135-147.

[11] Pottmann H, Lü W, Ravani B. Rational ruled surfaces and their offsets [J]. Graphical Models and Image Processing, 1996, 58(6): 544-552.

[12] 刘利刚, 王国瑾. 基于球面三角网格逼近的等距曲面逼近算法[J]. 工程图学学报, 2000, 21(3): 70-75.

[13] Sánchez-Reyes J. The symmetric analogue of the polynomial power basis [J]. ACM Transactions on Graphics, 1997, 16(3): 319-357.

[14] Sánchez-Reyes J. Applications of the polynomial s-power basis in geometry processing [J]. ACM Transactions on Graphics, 2000, 19 (1): 27-55.

[15] 苏本跃. 基于三角多项式曲线曲面的几何造型理论与方法研究[D]. 合肥: 合肥工业大学, 2007.

Rational Approximation of Offset Surface by Univariate S-Power Basis

ZHANG Li1,2, TAN Jie-qing1,2, LIU Zhi1,2
( 1. College of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China; 2. Department of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China )

A new algorithm for approximating offset surfaces by using univariate symmetric power basis is presented. It uses symmetric power basis to approximate u directional curves of tensor product Bézier surface, then it gets a set of offset approximating curves. From fixed v value of these curves, it will get a set of data points. The paper gets v directional approximating curves which get through these data points by anti algorithm of control points. Finally, rational approximating offset surface is got by using skinning surface algorithm. The algorithm is easy and solves the integral tolerance. Numerical examples show that it can achieve good effect with the raise of the S-power basis’ degree.

computer application; offset surface; tensor product Bézier surface; symmetric power basis; rational approximation; skinning surface algorithm

TP 391

A

：1003-0158(2010)01-0104-06

2008-07-16

国家自然科学基金资助项目（60773043；60473114）；安徽省自然科学基金资助项目（070416273X）；安徽省教育厅科技创新团队基金资助项目（2005TD03）；安徽省高等学校青年教师科研资助计划项目（2007jq1001）；合肥工业大学科学研究发展基金资助项目（061007F）

张 莉（1976-），女，安徽合肥人，副教授，博士研究生，主要研究方向为计算机辅助几何设计。