基于多结点样条的自由曲线最小误差逼近及其应用

余建德， 黄 静

（1. 澳门科技大学资讯科技学院，澳门；

2. 北师大珠海分校信息技术与软件工程学院，广东 珠海 519085）

基于多结点样条的自由曲线最小误差逼近及其应用

余建德1， 黄 静2

（1. 澳门科技大学资讯科技学院，澳门；

2. 北师大珠海分校信息技术与软件工程学院，广东 珠海 519085）

多结点样条函数具有良好的局部性，而最小二乘法对数据拟合的全局性较好， 因此多结点样条函数最小二乘逼近的稳定性及数值精度都能得到有效的保证。该文综合两者的特点，实现了自由曲线离散数据最小逼近误差数学模型的建立。同时应用此数学模型于一些平面及空间（甚至一些带噪音的）自由曲线拟合上和几何造型骨骼化上，测试其对各种自由曲线的拟合效果，结果证明最小逼近效果明显。

计算机应用；最小误差逼近；多结点样条；自由曲线

1 问题的提出

在实际应用特别是在反向工程中，对工件测量（数字化）之后得到的是一系列离散数据，为了实现工件的再加工或误差评定，必须对这些离散数据进行光滑而精确的曲线曲面重构，即数学建模。为实现高效率高精度光滑建模，以用于CAD/CAM 系统，研究曲线曲面最小误差逼近拟合建模具有重要意义。

在建模领域，通常使用B样条对曲线曲面进行插值建模[1-4]，而多结点样条近年来也因为它的各种优势而被广范用于插值法建模方面，且效果显著。多结点样条函数最早是针对插值问题提出的，1975年，齐东旭教授[5-7]给出了多结点样条基本函数的构造及计算格式；后继的文献[8-11]给出进一步的理论分析和应用。对插值问题而言，多结点技术的最大优点是导致插值过程无须求解任何方程组，而且插值格式具有局部性，这是与通常样条函数插值（三弯矩算法）在计算上的根本区别。被广泛应用的B样条曲线拟合方法虽然也不必求解方程组，也具有局部性，但在几何造型的应用中，因其无法保证通过型值点而给工程计算带来不便，因此多结点方法在工程应用上和理论研究上受到重视。

鉴于曲线建模是曲面建模的基础，本文研究这种甚具潜力的多结点样条拟合建模及其关键问题，实验表明，所建立的曲线拟合数学模型逼近拟合效果颇佳。

2 多结点样条函数

多结点基本样条函数是通过对等距结点 B样条基本函数的平移及迭加而构成。 记I为单位算子，μ为平均算子，对任意给定的常数 ξ，定义

图 1 多结点样条基本函数

多结点样条基本函数（见图1）的性质类似于B样条基本函数，其主要区别在于：不是非负函数，这将导致它构成的插值格式不是线性正算子，因此插值结果对数据而言不具有保凸性，这是追求显式解，局部性及基数型性质等优越性付出的代价。尽管如此，正如B样条基本函数插值对数据没有保凸性，但仍然实用一样，多结点样条插值也仍然是实用的，它已被成功地应用于飞机外形，进气道，机翼，海洋，地质的数据处理以及动画片的计算机制作等领域。

多结点技巧的意义首先在于构造显式插值格式。此外，基本函数的有界支集性质保证了插值曲线（面）的局部性，有利于数据处理，如果为整数结点上给定的数据，则多结点样条插值函数可写为

当给出确定的边界约束条件之后，即可明确给出求和的上下限，对于给定几何造型的型值点，其参数形式的多结点样条曲线定义为

3 多结点样条最小逼近误差拟合数学模型

（1） 数学模型的建立值得注意的是，由于多结点样条基函数的性质，使得该方程组的系数矩阵具有带状对角特点，条件数较好，方程组求解容易速度快，求出的系数为型值点的代表点。这一特点使得用多结点样条最小逼近误差拟合数学模型的方法优于其他方法。

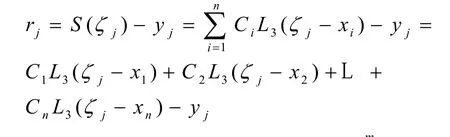
矩阵表达式为

4 实例分析及其应用

利用参数形式的三次多结点样条作最佳逼近的例子。

（1） 平面曲线的拟合（见图2）

下列两例子的原曲线参数方程分别为

图2 平面曲线拟合

从这两个例子表明，用多结点样条最佳逼近的拟合，对于带有噪音的平面离散数据，依然可以较好地重构原曲线（见图2），而且所使用的段数较少，只需16段，即17个拟合系数，即可较好地完成对1024个点的数据拟合。

（2） 空间曲线的拟合（见图3）

下列两例子(例1和例2)的原曲线参数方程分别为

图3 空间曲线拟合

图3(a)和图3(b)的4个图分别是原曲线，原曲线离散化（1024点），带噪音的离散点及 32段三次多结点样条拟合曲线；图3(c)和图3(d)的3个图分别是带噪音的离散点云数据，32段三次多结点样条拟合曲线及拟合后曲线的立体形状。例子表明，使用较少段数（这里是 32段）的多结点样条对于带噪音的空间离散数据，其拟合效果良好。

（3） 基于多结点样条最佳逼近骨骼化

设想几何造型是由它的骨骼和骨骼外围的噪音数据组成，那么骨骼化的过程就相当于去噪音的过程，只要选择好合适的段数，通过多结点样条最佳逼近来实现几何造型的骨骼化是可行的（见图4）。文献[15]应用及优化了组合模板的概念提出一种快速实用的细化算法，下面是该算法图4（中）与本文算法（右）的比较例子：

图4 几何造型的骨骼化实例比较

5 结 论

本文实现了多结点样条最佳逼近曲线建模，方程组因条件数较好求解容易速度快，求出的系数为型值点的代表点。这一特点使得用多结点样条最小逼近误差拟合数学模型的方法优于其他方法，具有很大灵活性。参数化的多结点样条最佳逼近对于平面及空间离散数据，甚至是带噪音的离散数据，拟合效果良好。应用多结点样条最佳逼近的去噪音性质，实验及证实多结点样条最佳逼近还具备对几何造形骨骼化的能力，其骨骼化效果满意。

[1] Toni Prahasto, Sanjeev Bedi. Optimization of knots for the multi curve B-spline approximation[C]// Proceedings of the Geometric Modeling and Processing 2000, Hong Kong, China. IEEE Computer Society, 2000: 150.

[2] Asif Masood, Muhammad Sarfraz, Shaiq A Haq. Curve approximation with quadratic B-splines[C]//Ninth International Conference on Information Visualisation (IV'05), 2005: 419-424.

[3] Byung-Gook Lee, Joon Jae Lee, Jaechil Yoo. An efficient scattered data approximation using multilevel B-splines based on quasi-interpolants[C]//Fifth International Conference on 3-D Digital Imaging and Modeling (3DIM'05), 2005: 110-117.

[4] Les A Piegl, Wayne Tiller. Approximating surfaces of revolution by nonrational B-splines [J]. IEEE Computer Graphics and Applications, 2003, 23(3): 46-52.

[5] 齐东旭. 关于多结点基数型δ-spline插值(I)[J]. 吉林大学学报(自然科学版), 1975, (1): 70-81.

[6] 齐东旭. 关于多结点基数型 δ-spline插值(II)[J]. 吉林大学学报(自然科学版), 1976, (2): 36-44.

[7] 齐东旭. 关于多结点基数型 δ-spline插值(III)[J]. 吉林大学学报(自然科学版), 1979, (3): 1-8.

[8] 齐东旭, 梁振珊. 多结点样条磨光(I)[J]. 高等学校计算器学学报, 1979, 1(2): 196-200.

[9] 齐东旭, 梁振珊. 多结点样条磨光(II)[J]. 高等学校计算器学学报, 1981, 3(1): 65-74.

[10] 齐东旭. 多结点样条插值曲线与曲面的矩阵表达式及余项估计[J]. 计算数学, 1982, 4(3): 244-252.

[11] 李华山, 丁 玮, 齐东旭. 多结点样条插值及其多尺度细化算法[J]. 中国图像图形学报, 1997, 2(10): 701-706.

[12] LeBourgeois F, Emptoz H. Skeletonization by gradient regularization and diffusion[C]//Ninth International Conference on Document Analysis and Recognition (ICDAR 2007) Vol 2, 2007: 1118-1122.

[13] 唐 瑶, 张锡哲, 王钲旋. 一种中国书法作品的骨架提取算法[J]. 工程图学学报, 2006, 27(5): 98-104.

[14] Takuya Oda, Yuichi Itoh, Wataru Nakai, et al. Interactive skeleton extraction using geodesic distance[C]// 16th International Conference on Artificial Reality and Telexistence—— Workshops (ICAT' 06), 2006: 275-281.

[15] 梅 园, 孙怀江, 夏德深. 一种基于改进后模板的图像快速细化算法[J]. 中国图像图形学报, 2006, 11(9): 1306-1311.

Least Error Approximation and Its Application for Free-Form Curves Based on Multi-Knots Spline

U Kin-Tak1, HUANG Jing2
( 1. Faculty of Information Technology, Macao University of Science and Technology, Macao, China; 2. College of Information Technology and Software Engineering, Beijing Normal University, Zhuhai Campus, Zhuhai Guangdong 519085, China )

Muti-knots spline has good locality and least square method has good global characteristics for data fitting. Therefore, the stability and numerical accuracy of least square method based on multi-knots spline approximation could be reached effectively. This paper combines the advantages of them and completes the model building of the free-form curves with least approximation error based on multi-knots spline. Meanwhile, this method is applied to the free-form-curve fitting of some plane and space (even with noise) data and Geometry Shape Skelectonization. The fitting results show that the least approximation effect is good.

computer application; least error approximation; multi-knots spline; free-form-curves

TP 391.41

A

：1003-0158(2010)01-0088-06

2008-08-05

澳门科技发展基金资助项目（018/2005A，045/2006A）；北京师范大学珠海分校重点资助项目（Z06007）

余建德（1973-），男，广东中山人，讲师，博士研究生，主要研究方向为数字信号处理算法。