参数化有限元分析的液压机机身轻量化设计

赵 韩， 陈兴玉， 董玉德， 张 坚， 余来宏

（1. 合肥工业大学机械与汽车工程学院，安徽 合肥 230009；2. 合肥压力机械有限责任公司，安徽 合肥 230031）

参数化有限元分析的液压机机身轻量化设计

赵 韩1， 陈兴玉1， 董玉德1， 张 坚2， 余来宏2

（1. 合肥工业大学机械与汽车工程学院，安徽 合肥 230009；2. 合肥压力机械有限责任公司，安徽 合肥 230031）

建立了液压机机身的参数化有限元模型。通过正交试验模拟实际工况进行了应力和角变形的分析计算。从试验样本出发，采用基于最小二乘法的回归模型构建了机身最大应力及角变形与结构主参数间的映射关系。在库恩-塔克条件下构造了优化的数学模型，并通过仿真运算提出了合理的机身轻量化设计方案。结果表明，轻量化效果明显，改进后的方案能完全符合实际工况的要求。

计算机应用；轻量化设计；最小二乘回归；液压机机身

机身是开式单柱型液压机的基本部件，工作时要承受全部工作变形力[1]。因此，机身的合理设计对减轻液压机重量，提高液压机刚度以及减少制造工时，都具有直接影响。为了降低液压机的材料成本，文献[2]和[3]分别探讨了开式机身的结构分析方法，并根据应力及角变形结果对结构进行了初步改进。但已有的研究尚未深入讨论机身在载荷作用下受力及角变形的规律。

为了探索机械结构应力应变规律，并在此基础上进行结构的轻量化设计，赵韩教授在ANSYS环境下对半挂式汽车车架结构进行了轻量化设计[4]；邓江华等运用神经网络和遗传算法构建客车车身骨架结构优化模型实现车身的轻量化[5]。本文则根据液压机机身主要由板材焊接而成的结构特点以及函数关系简明的工程要求，通过构建结构主参数与应力、应变等之间的线性回归模型，实现机身结构的轻量化。

1 机身参数化有限元分析

1.1 机身参数化实例构建

机身结构模型的参数化，有利于模型的快速变型，适用于正交试验时，每次试验中不同尺寸有限元模型的快速建立，节省了优化分析的时间。基于商用CAD软件SolidWorks的底层开发接口，并利用VC++语言，对机身构成组件以及整个模块模型进行尺寸重构。有限元分析时，为了避免模型转换时的特征丢失，采用与SolidWorks软件无缝集成的有限元分析插件CosmosWorks进行液压机机身的静应力分析和验证。图1所示为单柱型液压机机身各个构成组件间的装配约束关系。

（1） 零件重构 对于零件级别的参数化，事先需预定义好零件模型各尺寸之间的约束关系。定义约束关系的原则为：① 添加完全的尺寸约束；② 在保证完全约束的前提下，尽量减少尺寸的个数；③ 添加的尺寸约束应便于驱动；④ 驱动过程中，不能出现零件模型与设计意图相违背、特征悬空等错误。获得驱动尺寸，并进行修改的部分代码如下：

//获得工作台草图1中D2尺寸

ModelDoc→IParameter(_T("D2@草图 1@Y30-10A-1001.03工作台.SLDPRT"), &dimension);

//对该尺寸参数值进行修改，重新赋值为a，a为客户需求尺寸值

Dimension→SetSystemValue2(a,swSetValue_ Successful,&retval1);

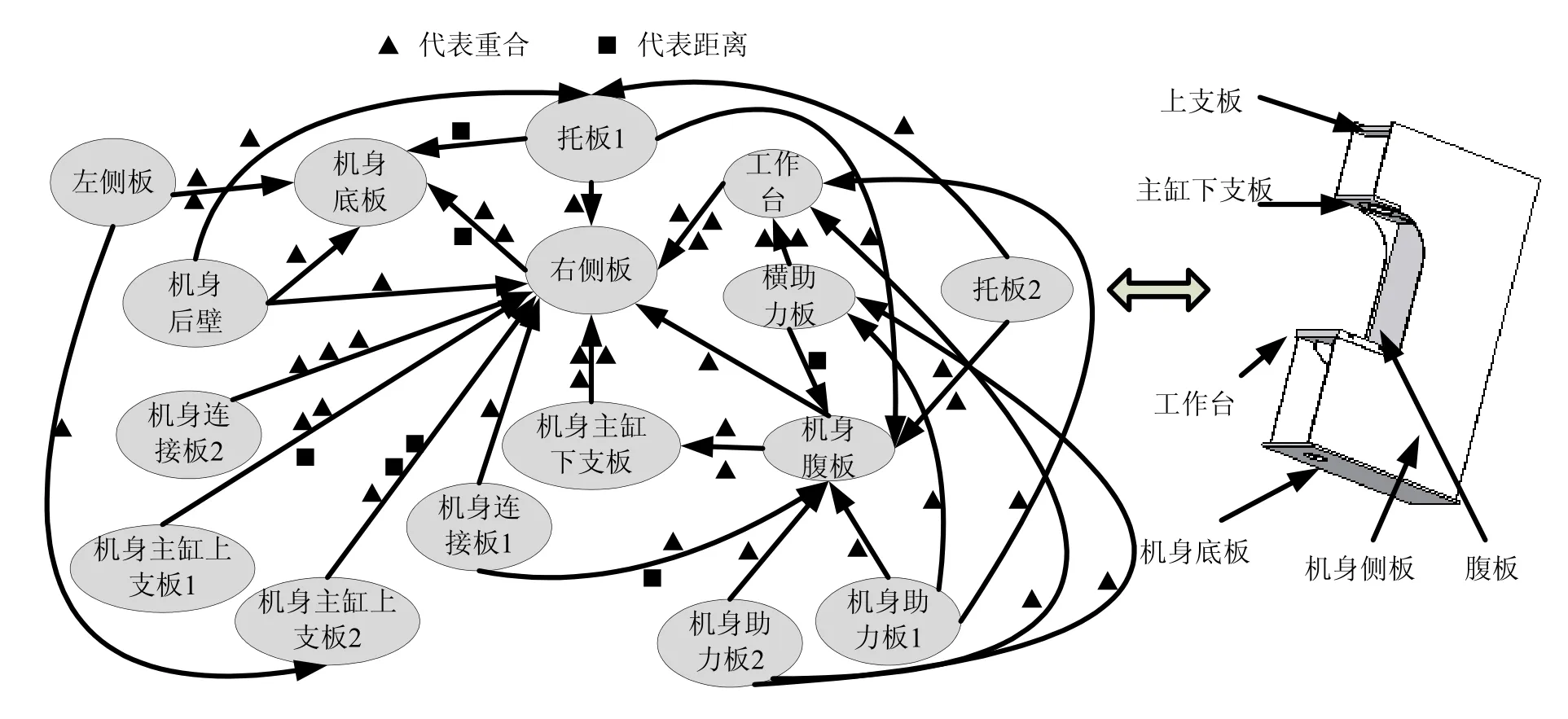
图1 机身参数化模板

（2） 装配体重构 对于装配模型的重构，涉及到装配体构成组件间尺寸约束关系的解决。定义组件之间的尺寸约束关系，可通过SolidWorks的方程式功能实现。图2为YH30型液压机机身装配体组件尺寸约束方程式。由影响应力和角位移的主要组件尺寸参数作为主变参数，首先进行相关组件的重构，然后再利用底层接口函数EditRebuild3()实现整个装配体的重构。

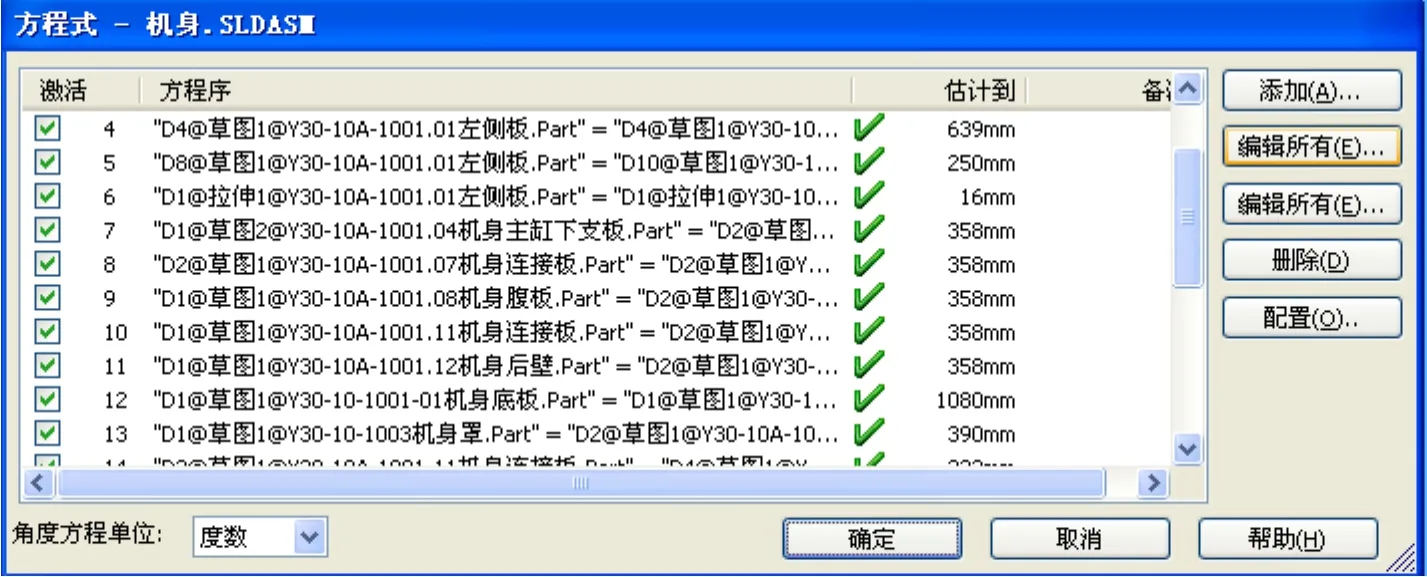
图2 YH30液压机机身方程式

1.2 机身结构静力分析

机身具有一上缸，可完成压装或校直工艺，其压装或校直力为10吨。机身的底面通过地脚螺栓与地面联结。因此，在计算时可将其当作开口钢架，危险截面在工作台及其与喉口连接处的截面及机身主缸上支板的液压缸安装处。因为C型机身是开口钢架，所以工作时会发生垂直变形进而导致角变形，致使上下支板、侧板和底座之间发生倾斜。这些变形将影响液压机压装和校直精度、加快模具磨损。为了保证所研制的这款液压机的可靠性、系统的准确性和经济性，有必要对其结构进行分析和校核，为进一步完善和优化结构设计奠定基础。

根据机身的结构形式和受力特点，选取实体网格，环数为3，雅各宾式检查为4点。机身材料为Q235碳素钢，弹性模量E=2.06E5MPa；泊松比μ =0.3，屈服应力[σs] =235MPa。液压机所受最大载荷即公称力为100kN，该力的作用通过液压缸与机身装配处传到机身上。因此，可以把公称力平均分解到安装液压缸位置的锪孔底平面和工作台面上，并对机身底部的所有自由度进行约束。图3所示为单柱型液压机机身的有限元模型。

2 正交试验设计

2.1 确定因素、水平和指标

（1） 试验指标和因素的选取

优化分析计算时，选取液压机机身的最大应力、最大角变形以及机身重量为正交试验的试验指标。影响试验指标的因素有很多，由于机身的结构限制较大，仅以腹板厚度（X1）、侧板厚度（X2）、工作台厚度（X3）、下支板厚度（X4）和肋板厚度（X5）为考虑因素，忽略其它因素的影响，见图4、图5和图6。

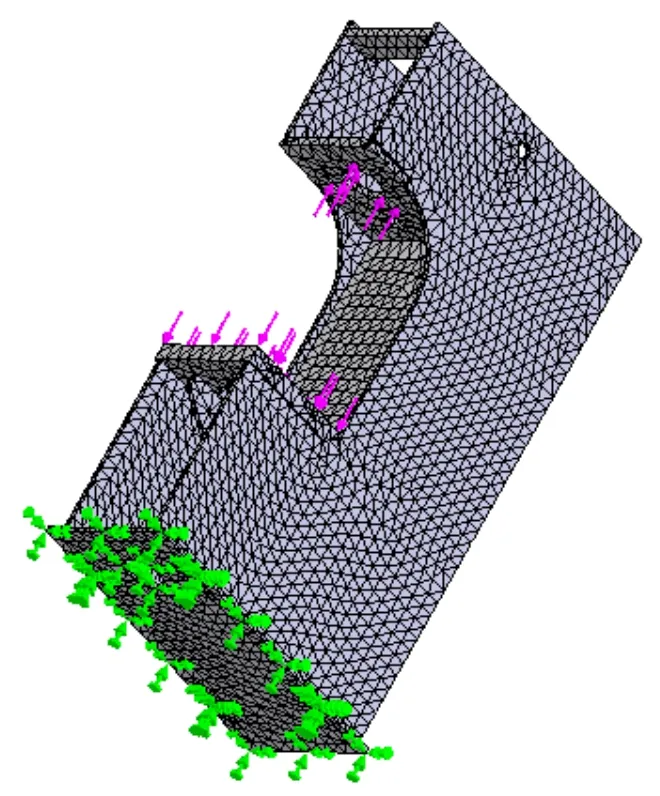
图 3 YH30型液压机有限元模型

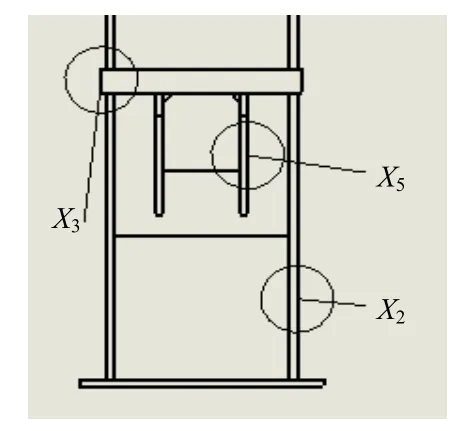
图 4 下梁截面

图 5 立柱截面

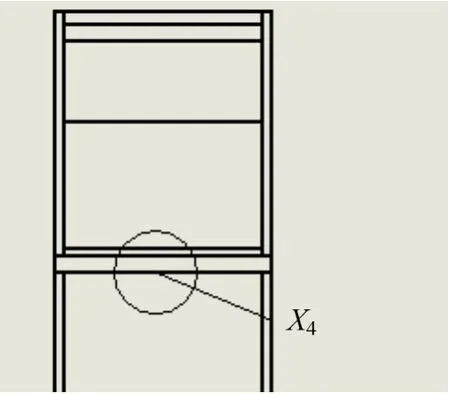
图 6 上梁截面

（2） 水平的确定

为了便于衡量各因素对试验指标的影响，选取最初的设计尺寸作为基本尺寸，各尺寸以基本尺寸为基准上下变动，变化幅度大致相等，可以获得表1。

2.2 试验分析结果

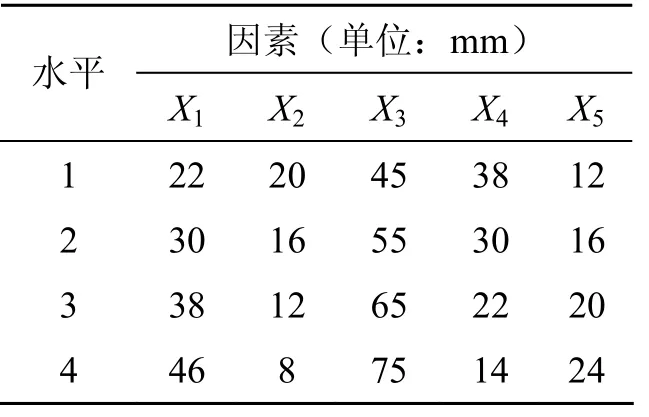
表1 试验因素水平表

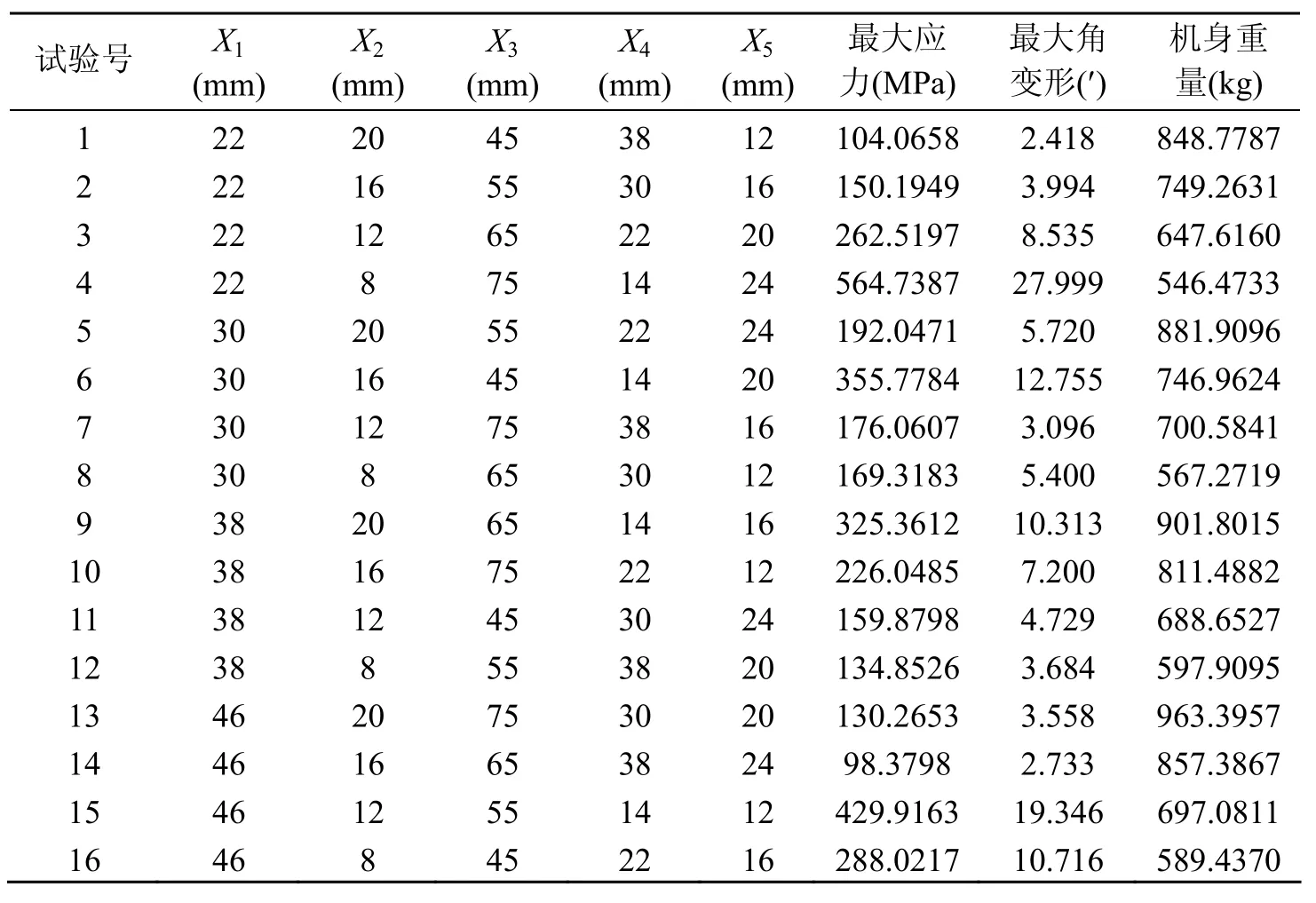
表2 正交试验计算结果

2.3 回归函数的构造

根据试验结果，应用最小二乘法原理构造正规方程[6]，代入试验数据仿真计算得机身最大应力、最大角变形和机身重量与结构主参数的回归系数分别为表3～表5所示。

表3 最大应力回归系数表

表4 最大角变形回归系数表

表5 机身重量回归系数表

3 机身的优化

3.1 设计变量

设计变量为腹板厚、侧板厚、工作台厚、下支板厚和肋板厚，即X={X1, X2, X3, X4, X5}。各变量所代表的尺寸如图4、图5和图6所示。

3.2 目标函数建立

对于液压机机身的轻量化设计，其目标函数就是在保证应力和角变形都符合的前提下，重量最轻。所以目标函数为

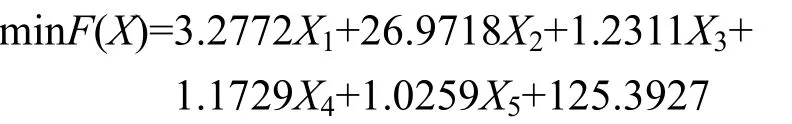
3.3 约束函数

由行业设计规范知，在减轻机身重量的同时，必须要满足机身的应力和角变形限制需求：

（1） 强度状态变量及约束函数

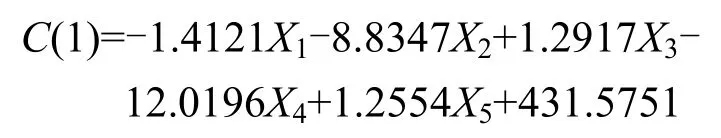
（2） 静刚度状态变量及约束函数

式中 [δs]为最大角变形限值，由行业规范取为6′

（3） 几何约束

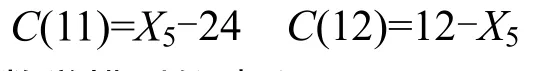
3.4 数学模型的建立

根据前面构造的目标函数和约束函数，得出机身轻量化设计的数学模型为

设计变量 X={X1, X2, X3, X4, X5}

约束方程 Ci(X )≤0 (i=1, 2, ……, 12)

目标函数 minF(X)=3.2772X1+26.9718X2+ 1.2311X3+1.1729X4+1.0259X5+125.3927

3.5 轻量化计算

由优化设计知识中的库恩—塔克条件(λ为拉格朗日乘子)

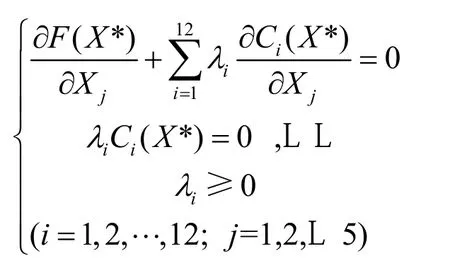
利用matlab软件的优化设计工具包，可方便计算出优化结果，再根据板材的型号加以圆整后最终取：X1=25mm、X2=11mm、X3=45mm、X4=36mm、X5=15mm。

4 结果分析

根据轻量化结果，利用CosmosWorks进行仿真验算与分析，看其结果是否满足液压机机身的使用要求。经过分析，得出改进后机身结构的应力值在许用范围内，并且机身主缸下支板的角变形在6′之内，完全符合实际工作工况的要求。

表6列举了方案在改进前和改进后的对比情况，从重量、应力和角变形3个方面进行了比较。由表6可以看出，本文所用的轻量化方法效果明显，可以给企业带来一定的效益。

表6 方案改进前后对比

5 结 论

通过对液压机机身进行参数化有限元分析，提取出机身结构的相对薄弱环节以及影响的主结构参数，并基于构建的目标参数与结构主参数间的线性回归模型，对整个机身进行了轻量化优化设计。从轻量化结果可知，原机身的重量、应力和角变形都有不同程度的减少，重量减轻最明显，为企业节省了材料和运输等费用，使得结构设计更加合理。下一步的工作将进行液压机的动力学仿真，建立仿真模型，进而模拟其实际工作的过程。

[1] 俞新陆. 液压机的设计与应用[M]. 北京: 机械工业出版社, 2007. 315-326.

[2] 刘 茜, 董正身, 卞学良. 基于ANSYS的C型液压机机身有限元分析[J]. 机械设计与制造, 2006, (4): 21-22.

[3] 宋雨芳, 吴友坤, 荣兆杰. 基于有限元基础的单柱液压机机身的优化设计[J]. 锻压装备与制造技术, 2005, (5): 29-30.

[4] 赵 韩, 钱德猛. 基于ANSYS的汽车结构轻量化设计[J]. 农业机械学报, 2005, 36(6): 13-15.

[5] 邓江华, 刘献栋, 冯国胜. 基于神经网络和遗传算法的车身骨架结构优化设计[J]. 农业机械学报, 2007, 38(6): 26-29.

[6] 何晓群, 刘文卿. 应用回归分析[M]. 北京: 中国人民大学出版社, 2001. 18-121.

Research on Lightweight Design of Press Frame Structure Based on Parametric FEA

ZHAO Han1, CHEN Xing-yu1, DONG Yu-de1, ZHANG Jan2, YU Lai-hong2
( 1. School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei Anhui 230009, China; 2. Hefei Pressure Machinery CO., LTD, Hefei Anhui 230031, China )

The parametric finite element model of hydraulic pressure (HP) is built. Also, orthogonal experiment is used to simulate actual work condition for calculating stress and angular distortion. Using data from related experiments, the linear relation between HP’s main structural parameters and its maximal stress, maximal angular distortion and weight is get according to the regression model. The regression model is established based on least square method. Under Kurd-Tark condition, the optimal mathematic model is built. Also, reasonable lightweight design plan is proposed through simulative calculation. It is showed that the effects of lightweight design are obvious, the improved plan is in accordance with actual work condition.

computer application; lightweight design; least square method; hydraulic pressure

TP 391.72

A

：1003-0158(2010)01-0020-06

2008-04-07

国家科技攻关计划资助项目（2005BA201A83-01）；合肥市重点科研资助项目（2007（1007））

赵 韩（1957-），男，安徽宿州人，教授，主要研究方向为电动汽车、机构设计、产品的数字化设计。