一种多源协作网络的分布式功率分配与中继选择算法

惠 鏸 朱世华 吕刚明 孙晓东

①(西安交通大学电子与信息工程学院 西安 710049)

②(西安理工大学自动化与信息工程学院 西安 710048)

1 引言

协作通信技术可以通过用户之间共享天线，构成虚拟多天线阵而获得空间分集，从而有效对抗信道的多径衰落，提高传输质量，近年来受到广泛关注。文献[1,2]最早提出了用户协作的概念以及基本的协作通信协议，奠定了协作通信的研究基础。由于在无线协作通信网络中，系统一般具有资源受限的特点，因此如何对有限的资源进行合理分配，以获得更好的系统性能一直是协作通信领域的研究热点之一。文献[3]针对解码转发(Decode-and-Forward，DF)协作通信网络，提出了一种在满足一定中断概率条件下最小化系统发射总功率的算法。Bletsas等人[4]提出了一种机会式的中继选择方法，通过选择一个“最优”中继进行信息转发，获得与分布式空时码(Distributed Space Time Coding,DSTC)相同的分集性能。然而这些文献的研究工作一般针对系统中只存在一个源-目的节点对展开。随着研究的深入，考虑到多个源节点同时需要进行信息传输的场景在实际系统中更为常见，出现了针对多源协作通信系统的研究。文献[5,6]指出，合理地设计协作策略可以使多源协作通信系统获得满分集增益，例如多路信号在接收端的合并可以采用正交传输及最大比合并(Maximum Ratio Combination,MRC)，以及复域编码等。针对多源协作场景，文献[7]提出了一种使用解码转发的中继选择算法，每对源-目的节点选择一个中继进行转发，并证明该算法比采用DSTC具有更好的中断概率性能。文献[8]则针对DF协作系统，提出了一种中继选择和功率分配算法，在保证系统满足一定中断概率的条件下最小化系统传输所需要的总功率。不过，对于采用放大转发(Amplify-and-Forward, AF)的多源协作通信，目前在功率分配方面的研究并不多见。

在上述研究的基础上，本文在多源协作背景下，针对放大转发协作通信网络，提出了一种分布式的功率分配与中继选择算法。所提算法在保证系统满足一定中断概率的条件下，有效降低了传输所需的总功率，同时与集中式方法相比显著节约了系统的控制开销。

2 系统模型

多源协作通信网络如图1所示，网络中有M个源节点和N个中继节点，且M≤N。将源节点与中继节点集合分别定义为S和R。中继可以在网络中预先放置，也可以是暂时没有信息需要发送的空闲节点。与文献[8]相同，假设一次传输中每个源选择一个中继为其转发信息。传输过程分两个阶段进行：第1阶段，各个源分别在正交的(如时分)信道上广播信息；第2阶段，完成选择后，各中继协助其对应的源节点向目的节点进行转发。第1阶段中继j,(j∈R)收到的来自源节点i,(i∈S)的信号和第2阶段目的节点收到的中继j所转发的信号分别为

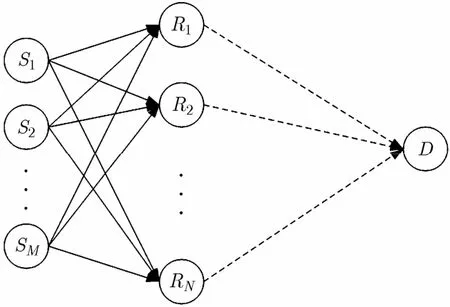
图1 协作通信网络模型

其中xi、xj分别是源和中继节点功率归一化的发射信号，Psi和Prj分别表示源节点i和中继j的发射功率，hij与hjd分别表示源节点i与中继j之间以及中继j与目的节点之间的信道衰落系数，它们都是相互独立的零均值循环对称复高斯随机变量，其方差分别为λij和λjd，信道慢衰落。nij与njd是独立的零均值加性高斯白噪声，不失一般性，假设其噪声功率谱密度为1。

采用放大转发协议，为满足发射功率的限制，将xj的功率归一化，即

则目的节点的接收信噪比可以表示为

则认为目的端可以正确解码，传输成功，否则出现中断。

由以上描述可以看出，若系统中任意两节点间的信道衰落系数已知，源与中继节点可以通过调整自己的发射功率来保证系统的中断概率为0。但这要求源与中继节点都已知各链路信道衰落系数的实时值，将导致巨大的系统开销，在网络中节点个数较多时尤其难以实用。因此，本文中假设源与中继节点都已知部分信道状态信息(Channel State Information, CSI)[3]，即对源节点i来说，它只已知自身到各中继节点的信道衰落系数 {hij}，以及中继到目的节点信道状态信息的统计特征{λjd}。对中继j来说，它同样知道源节点到自己的信道衰落系数{hij}，并且知道自己到目的节点的信道衰落系数hjd，但它无需知道源到其它中继的CSI。即各节点知道与自己直接相连的信道的衰落系数，但对于其它节点间的信道只需知道其统计特性，或者无需获知，这样就大大减少了传输CSI的负担。

3 中继选择与功率分配

不失一般性，假设系统对各个源-目的传输链路的中断概率要求均为ρ，此时最小化系统传输总功率的问题可表示为

以求解式(6)为目标，本节将首先研究单个源节点多个中继情况下的功率分配与中继选择问题，然后在讨论针对多源多中继的集中式控制方法的基础上，最终提出本文的分布式控制方案。

3.1 单个源节点时的功率分配与中继选择

首先考虑当系统中只有一个源i要发送信息，即M=1的情况。此时问题式(6)可表示为

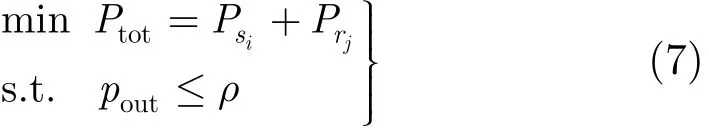
由式(4)，式(5)可知，为满足目的端的信噪比要求，当源节点的发射功率为Psi且选择中继j为其转发时，中继节点的发射功率必须满足

当源-中继-目的链路总发射功率最小时，式(8)中等号成立。显然，若，中继的发射功率为负，这意味着中继无论以多大的发射功率转发都无法满足目的节点的信噪比要求，选择此中继没有意义，为此，定义源i(i=1,2,…,M)的可靠节点集合为

只有集合iA中的节点才能作为中继向目的节点转发信息。

在传输的第2阶段，为保证式(8)所示的中继发射功率为有限值，令只有当时，中继节点才会向目的节点转发信息。由于源节点已知源-中继的信道衰落系数，因此它可以以一定的功率发送信息以保证源-中继链路无中断，但由于它不知道中继-目的节点的信道衰落系数，因此无法保证中继能够成功地向目的节点转发信息，而是需要根据hij和λjd来决定其发送功率Psi及其相应的中继转发门限ζ，以保证在系统满足一定中断概率的条件下，所需要的链路发射总功率的均值最小。此时问题转化为

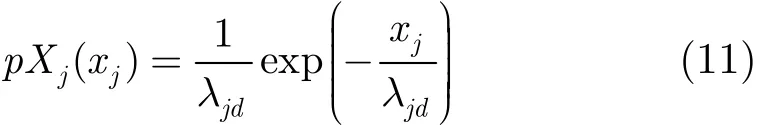
因此，中继j的发射功率期望可表示为

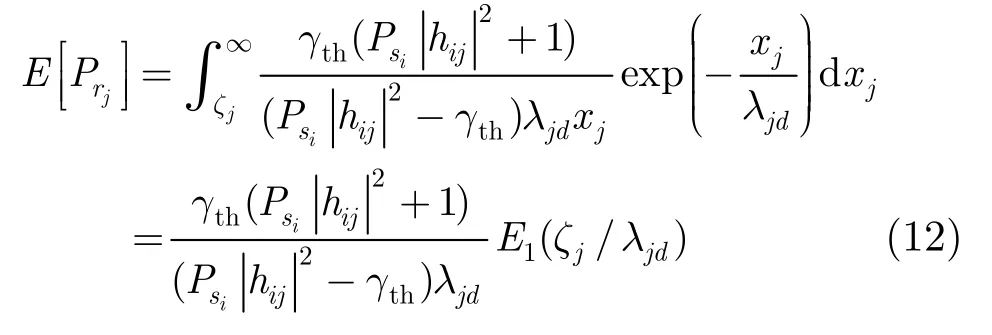
由此可以得到

将式(16)代入式(15)可以得到选择某个中继j时的平均总传输功率E[Ptot]，由此选择

源节点在发送信息时，可将其选择的中继及其转发门限一同广播，被选中的中继节点根据转发门限自主判断是否进行转发。至此我们得到了当系统中只有一个源节点要发送信息时，中继节点的选择方法以及源与中继的功率分配方法。

3.2 多源多中继场景下分布式节点选择与功率分配

当系统中存在多个源节点需要发送信息时，对每个源节点都可依照3.1节中的方法计算出该源节点选择不同中继时该源-中继-目的链路传输所需要的最小总功率的期望值。建立矩阵PM×N

其中Pij表示源节点i发送，中继节点j转发信号时所需要的最小链路发送总功率的期望。

可以看出，穷举所有源与中继的组合，得到所需要的系统发送总功率，从中选取总功率最小的组合，即可获得最优解。因此，穷举方法的结果可以视作总发射功率的下界，但其复杂度为N!/(N−M)!，当M，N较大时在实际系统中很难实现。为此，文献[8]就针对类似问题提出了一种复杂度为O(M(N+1))的节点选择方案，具有较好的性能。而另一方面，根据离散数学中对于二分图的研究可知，采用匈牙利方法(Hungarian method)[9]，可以使问题能够在多项式时间内求解并且所获解与穷举方法完全相同，也是同等条件下所获得的最优解。然而，上述3种方法存在一个共同问题：功率分配和中继节点选择都需要在中心节点的集中控制下完成。这将给系统带来极大的开销。

为此，本文提出分布式的节点选择与功率分配算法，算法由源节点自主选择中继，中继收到来自源节点的信号后，根据转发门限自主判断是否进行转发，进而完成整个传输。为了避免各个源所选择的中继相同而产生冲突，在这一过程中引入定时器。

用r(si)表示源i所挑选的中继，若系统中有多个源选择同一个中继进行转发，则该中继以相等的概率为其中某个源进行转发，其余源节点发送失败。定义C (si)={j| r(sj)=r(si),j∈S }表示与源i选择同一中继的所有源节点的集合；B(si, l)={C(si)=l }表示系统中包括源i，一共有l个源节点选择r(si)作为中继的所有C(si)的集合，表示集合C(si)中节点的个数。则对任意源i来说，所选中继不能为它转发的概率η为

可以看到，在分布式的中继选择方法里，由于存在发生冲突的可能性，此时系统的中断概率已不能简单地用式(12)表示。用ε=1−exp(−ζj/λjd)表示不考虑多个源选择同一中继的情况下链路的中断概率，则ρ、ε与η的关系可表示为

由式(20)可以看出，ρ随着η和ε的增加而增加，且ρ≥max(η, ε)。也就是说，在ε一定的情况下，多个源选择同一中继的概率η是系统性能的瓶颈。因此，要保证较低的中断概率，必须同时保证较低的η和ε，这就要求在分布式的场景中，η尽可能趋于零。

为了满足这一要求，需要为各源节点设定时器竞争中继，定时器最先到时的源优先选择中继，其余源不再使用该中继。设计定时器应考虑以下关键因素。首先，定时器显然应保证耗费链路总功率小的源-中继在竞争中具有优势。但如果只考虑这一点，当M=N时，最后进行选择的源只剩下一个中继可供选择。如果该源-中继之间的信道处于深衰落，将导致源必须以极大的功率发送以达到中断性能要求，从而导致系统传输总功率较大。为避免这种情况的出现，定时器的设定还应考虑如果某源节点不能竞争获得某中继而选择其它中继的代价。基于以上考虑，本文提出如下利用定时器避免冲突的分布式算法。

初始过程：各源按3.1节的方法得到自己选择不同中继时所需要的链路总功率期望值的矩阵。初始源节点集合为S={1,2,…,M}，待发送信息源节点的个数=M，初始备选中继节点集合为R ={1,2,…,N}。

第1步 各源节点设定定时器。以源节点i为例，该过程可描述为

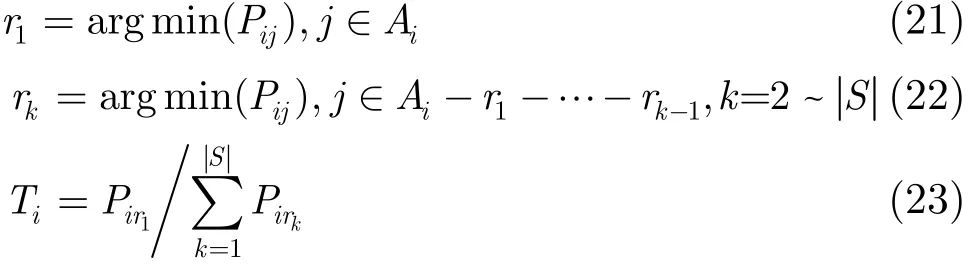
其中rk为所需链路总传输功率第k小的中继，Ti为源节点i的定时器的设定值。也就是说，各源从备选中继节点集合R中挑选所需链路总传输功率最小的个中继，并按式(23)设置定时器的值。观察式(23)，其分子表示，当源节点i选择其当前最优中继时，所需要的链路总功率越小，Ti就越小，该源竞争获得该中继的可能性越大。由于系统中一共有个源要进行传输，因此在最差的情况下，该源会选择r为其转发，式(23)的分母表示所有可能被选择的中继所需要的链路总功率之和。这个值的大小在一定程度上说明当不能选择当前最优中继时，选择其它中继可能需要的功率大小。因此这个值越大，Ti就越小，同样该源竞争获得当前最优中继的可能性越大。

第2步 各源节点竞争其转发中继。也就是说，定时器的值最小的源i*=minTi, i∈S优先选择中继节点。由于无线信道的广播特性，其余源节点可以获得这一信息，并更新此时的待发信息源节点集合以及备选中继节点集合。

第3步 当S=∅时，中继选择过程结束，源节点在其发射信息中指明所选中继，各中继按照式(8)为指定的源转发信号；否则转到第1步。

通过以上步骤可以看出，由于定时器Ti是相互独立的连续随机变量，因此任意两个源选择同一个中继的概率Pr(Ti=Tj,∀i, j=1,…,M,i≠j)=0。结合式(19)可知Pr(η=0)=1，也即所提算法由于选择中继而导致冲突的概率η趋近于0。

4 仿真结果及分析

本节对所提出算法的性能进行了蒙特卡罗仿真。仿真中设置目的节点的目标信噪比为γth=10dB，两节点间信道衰落系数的方差λij=，其中dij为两节点i，j之间的距离，c为常数，α为路径衰落系数。不失一般性，仿真中取c=1，α=3。假设源-中继及中继-目的之间的距离较远，而各源节点之间、中继节点之间的距离相对较近。因此各源节点与各中继节点间的距离近似相等用dsr表示，各中继-目的节点间的距离也近似相等用drd表示，各源与目的节点之间的距离近似相等用dsd表示。为了便于比较，本文还对集中式控制做了性能仿真，包括中心节点随机为每个源节点分配中继(保证为每个源所分配的中继为其可靠中继节点)的算法，以及采用了匈牙利方法的集中式最优算法。

图2比较了不同中断概率要求下几种算法所需的系统总发射功率。系统中源节点与中继节点的个数均为5个，中继节点位于源与目的节点的中间位置(dsr=drd=1)。从图中可以看出，本文算法所需要的系统总功率与集中式最优算法十分接近，而与各个源节点随机选择中继节点的算法相比，可以节约约50%的发射功率。

图3比较了本文分布式算法与集中式最优算法的性能。系统中源节点的个数M=3，中继节点的个数则分别取N=3,5,7，位于源与目的节点的中间位置。仿真结果表明，备选的中继数目越多，系统所耗费的总功率越小；同时随着备选中继节点数目的增加，本文算法与集中式控制算法所耗费的系统总功率更为接近。

考虑集中式与分布式算法的系统开销。在集中式算法中，需由中心节点完成功率分配和中继选择，并将最终结果反馈给各源和中继节点。在此过程中中心节点需要知道各源-中继的hij共MN个实时CSI，以及各中继-目的节点的{}共N个CSI统计值。需要反馈的信息包括各源节点的发射功率{}共M个，为各源节点选择的转发中继节点共M个，及各中继转发门限共M个。(为避免向中心节点反馈中继-目的节点的实时CSI，仍由各中继节点根据转发门限自主判断是否转发和计算发射功率。)与之相比，分布式算法只需中继节点向源节点反馈中继-目的CSI的统计特性{}共N个，而后各源向中继反馈的信息与集中式算法相同。这将显著节省系统开销。加之在仿真结果中，集中式与分布式算法的性能非常接近，因此本文的分布式算法在实际中更具应用价值。

为了进一步揭示本文分布式算法的性能，图4对中继靠近源节点(dsr=2/3，drd=4/3)，或目的节点(dsr=4/3，drd=2/3)的情况分别做了仿真。结合图2可以看出，在源与目的节点距离相同的情况下，当中继与目的节点距离较近时，本文的分布式算法与集中控制相比会有一定的功率损失。但是随着中继与源节点的距离由远及近，本文分布式算法与集中控制的性能也越来越接近。因此，本文的分布式算法在中继节点与源节点距离相对较近时性能更佳。

5 结束语

本文针对多源多中继的放大转发协作通信网络，在满足系统一定中断概率要求的前提下，以最小化系统总功率为目标，提出了一种分布式的功率分配与中继选择算法。源与中继节点均已知部分信道状态信息，源节点通过对发送信息所需链路总功率的期望的计算，选择最佳中继，并通过定时器的使用竞争中继的使用权。中继节点根据转发门限自主判断是否对源节点的信息进行转发。仿真结果表明，本文所提出的分布式算法能够有效降低系统发送所需要的总功率，与中心节点集中进行功率分配与中继选择所能获得的最优结果性能相近。由于分布式算法节约了集中控制所需的信令开销，因此本文算法更具应用价值。

图2 不同算法所消耗的系统总功率比较(M=N=5)

图3 备选中继节点个数对系统总功率的影响(M=3,N=3,5,7)

图4 中继节点位置对系统消耗的总功率的影响(M=N=5)

[1] Sendonaris A, Erkip E, and Aazhang B. User cooperation diversity-Part I and II [J]. IEEE Transactions on Communications, 2003, 51(11): 1927-1948.

[2] Laneman J N, Tse D N C, and Wornell G W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior [J]. IEEE Transactions on Information Theory, 2004,50(12): 3062-3080.

[3] Chen M, Serbetli S, and Yener A. Distributed power allocation strategies for parallel relay networks [J]. IEEE Transactions on Communications, 2008, 7(2): 552-561.

[4] Bletsas A, Shin H, and Win M Z. Cooperative communications with outage-optimal opportunistic Relaying[J]. IEEE Transactions on Wireless Communications, 2007,6(9): 3450-3460.

[5] Ribeiro A, Wang R Q, and Giannakis G B. Multi-source cooperation with full-diversity spectral-efficiency and controllable-complexity [J]. IEEE Journal on Selected Areas in Communications, 2007, 25(2): 415-425.

[6] Wang Tai-ran and Giannakis G B. Complex field network coding for multiuser cooperative communications [J]. IEEE Journal on Selected Areas in Communications, 2008, 26(3):561-571.

[7] Beres E and Adve R. Selection cooperation in multi-source cooperative networks [J]. IEEE Transactions on Wireless Communications, 2008, 7(1): 118-127.

[8] Si Jiang-bo, Li Zan, Dang Lan-jun, and Liu Zeng-ji. Joint optimization of relay selection and power allocation in cooperative wireless networks [C]. International Conference on Communication Systems, Guangzhou, China. Nov. 19-21,2008: 1264-1268.

[9] Dossey J A, Otto A D, Spence L E, and Eynden C V. Discrete Mathematics [M]. New York: Prentice Hall PTR, 2000:352-360.