流形及其子流形的Landsberg曲率关系

许 飞， 曹贻鹏， 张改平

（装甲兵工程学院基础部，北京 100072）

0 引 言

20世纪90年代末以后，经陈省身院士的大力倡导，Finsler几何的研究在国际和国内有了很大发展，特别是大量新的Finsler度量的发现和Finsler空间的整体性质的建立，使越来越多的学者更加关注Finsler几何的研究，同时，作为Finsler几何一个重要的研究方向，子流形也越来越受到重视。目前，很多工作都围绕流形和其子流形的曲率关系展开，例如 S曲率、旗曲率、Weyle曲率，并在此基础上得出很多好的结果，文中正是在上述背景下计算了流形及其子流形的Landsberg曲率关系。

1 Finsler几何

定义1[1-3]光滑流形M上的Finsler度量就是TM上的一个函数F:TM→[0，+∞），满足:

1）正则性:F在TM{0}上光滑;

2）一阶正齐次性:F（x，λ y）=λ F（x，y），∀λ＞0;

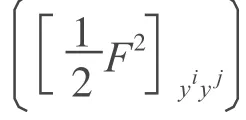
则称F是流形M上的Finsler度量，赋予Finsler度量F的光滑流形M称为Finsler流形。

若{ei}是拉回切丛π*T M的局部标架，定义π*TM上的线性联络▽

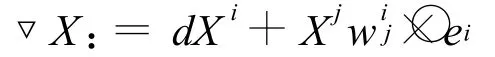
其中X=X′（x，y）ei∈C∞（π*TM），显然▽是π*TM上的线性联络。

又定义ρ:T（TM0）→π*TM是向量丛映射，且

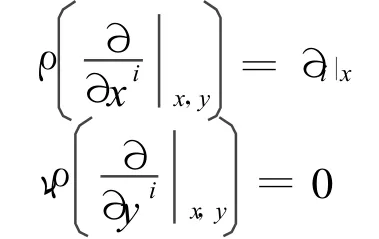
则

显然，▽是π*TM上的无挠联络，此时称▽是Chern联络。

Finsler几何子流形理论主要是通过将Riemann几何中子流形的理论推广到Finsler几何中，根本不同的一点是将切丛取代流形来作为底流形考虑的，在性质上此理论的缺憾在于:

1）计算麻烦，主要是形式比较复杂。

2）选用Chern联络时，其诱导的联络和子流形本身的Chern联络并不一致，后面将进一步给出两者的关系[4-5]。

命题1[6]设 HT M0=（）是Fm+n的非线性联络，则诱导的Fm非线性联络与Fm+n的非线性联络有如下关系:

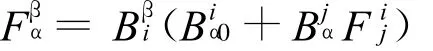
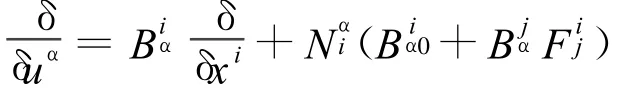
在TM0上存在着诱导非线性联络H TM0=），同时，本身TM0上有内蕴的非线性联络HTM*0=（F*βα），非常遗憾，这两者并不重合，它们有如下关系。

命题2[6]设Fm是Fm+n的子流形，则Fm诱导的和本质非线性联络有如下关系:

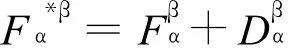
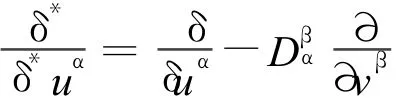
介绍齐性函数和基本张量，以简化后续的计算。

引理1 设V是一个向量空间，H:=V→R具有r阶正奇性，即对一切λ＞0，有

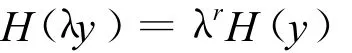
则

具体证明过程详见文献[5]。

下面计算Landsberg曲率关系。

2 Landsberg曲率关系的计算

定理1 设M是Finsler M的子流形，Lα βγ为子流形的 Landsberg曲率，Lijk为大流形的Landsberg曲率，它们的关系如下:

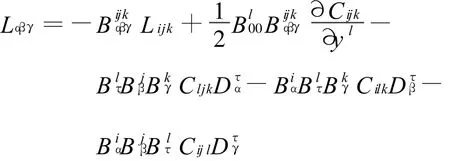
证明 设Fm是Fm+n的子流形，且Fm诱导的非线性联络为和本质非线性联络为，由命题1和命题2有:

下面计算流形Fm+n和子流形Fm的Cartan形式的关系:

将上两式相乘并轮换指标得:

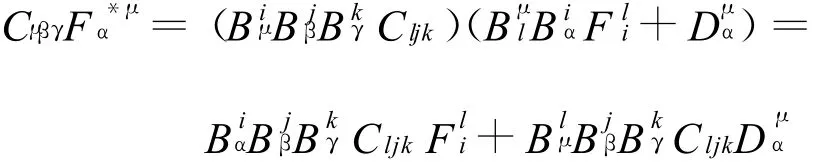
同理

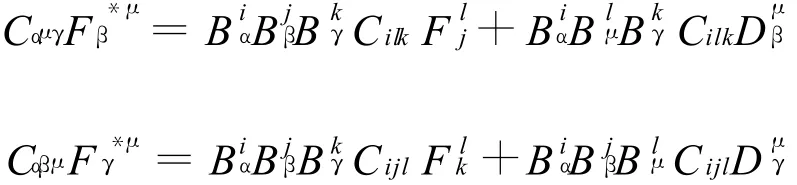
设 Gα是Fm的Spray系数，Gα是Fm+n的Spray系数，则它们的关系如下:

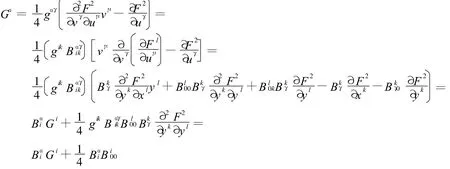
对上式的Cartan形式进行求导:

将上两式相乘并轮换指标得:

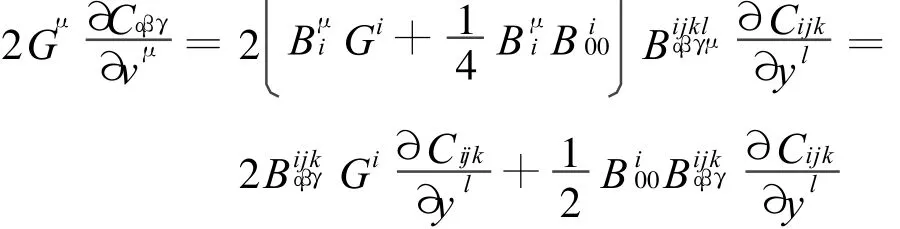
下面将上式各量依次代入子流形的Landsberg曲率公式。

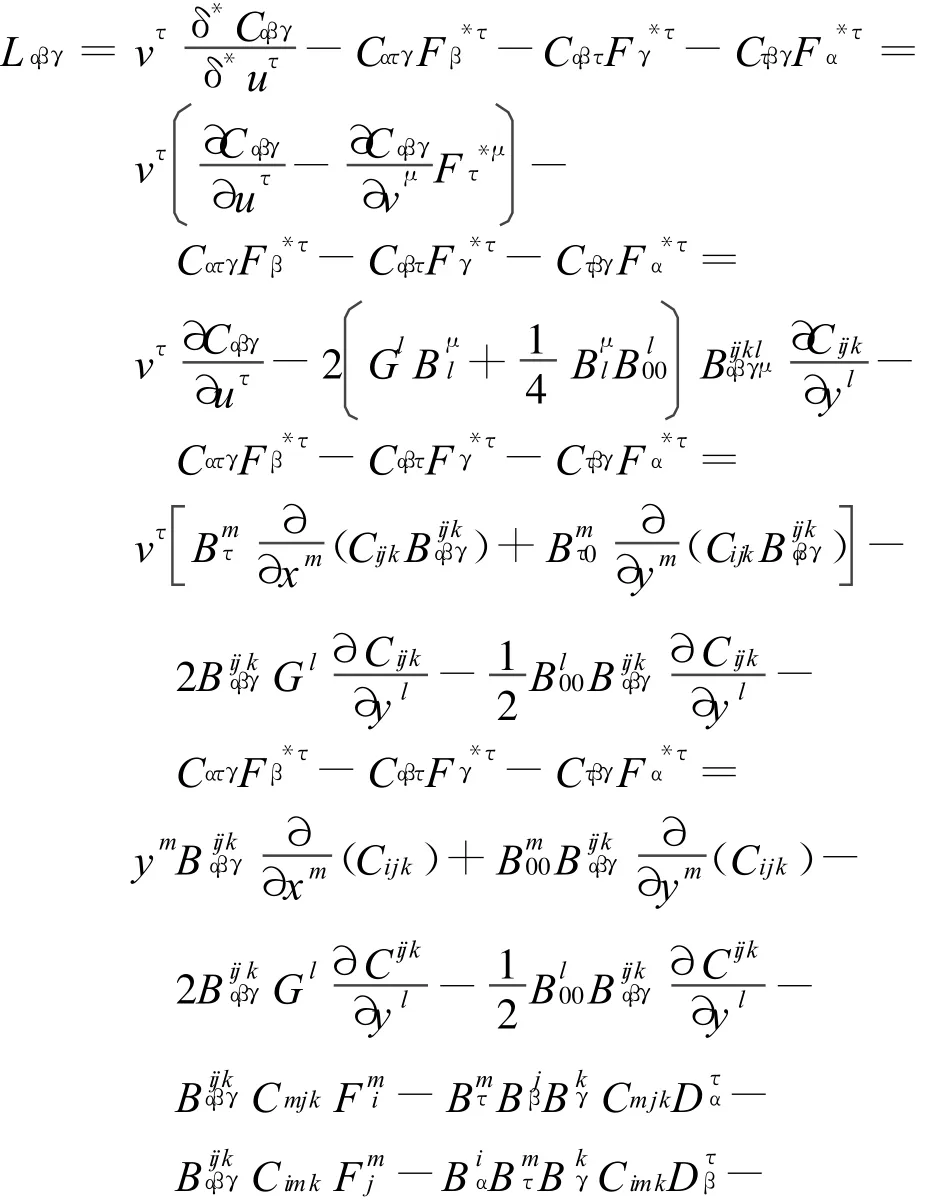
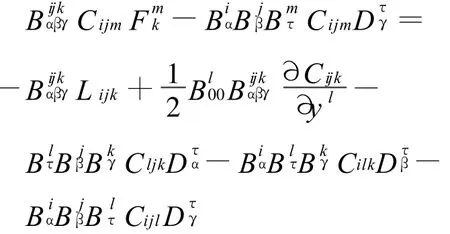
即

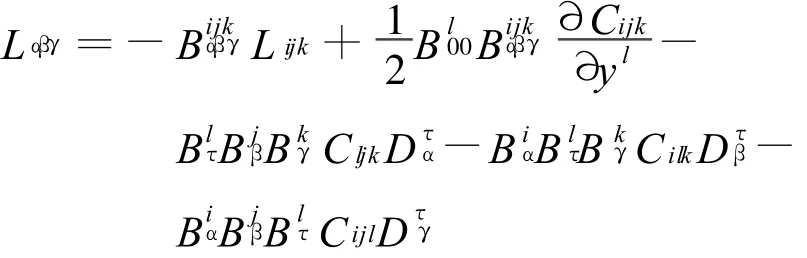
[1] Souza M，Spruck J，Tenenblat K A.Bemstein type theorem on a Randers space[J].Math.Ann.，2004，329（2）:291-305.

[2] Souza M，Tenenblat K.Minimal surfaces of retation in Finsler space with a randersmetric[J]. Math.Ann.，2003，325（5）:625-642.

[3] Mo X.An introduction to finsler geometry[M]. [S.l.]:World Scientific，2006.

[4] 莫小欢.黎曼-芬斯勒几何基础[M].北京:北京大学出版社，2007.

[5] 聂智，杨国俊.关于Finsler空间的子流形[J].重庆师范学院学报:自然科学版，1998，15（4）:16-20.

[6] Bejancu A，Farran H R.Geometry of pseudo-Finsler submanifolds[M].Wellington:Kluwer Academic Publisher，2000.