一种基于SVM的航路规划研究

程春华，吴进华，周大旺

（海军航空工程学院 a.研究生管理大队；b.控制工程系，山东 烟台 264001)

0 引言

航迹规划定义为在特定约束条件（包括环境约束和运动体自身约束）下，寻找运动物体从起始点到目标点，满足某种性能指标和某些约束的最优运动路线、路径[1-2]。对于反舰导弹，其航迹规划的目的就是通过规划对岛屿、陆地、警戒雷达区域或其他需要规避的区域进行规避，以达到避开岛屿攻击目标的作战目的。假设反舰导弹在遂行任务过程中保持高度不变、速度不变，而且考虑敌方防御区处于平坦地域，那么反舰导弹就无法利用地形因素进行威胁规避机动，航路规划问题就可以被简化成为一个二维航路（也就是水平航路）规划问题。很多学者通过对规划空间进行网格划分形成连接起始点和目标点的网络图[1-3]，然后采用搜索算法进行航路寻优。许多学者在这方面做了大量的工作，采用了许多智能搜索算法，如A*算法[4]、遗传算法[5]、蚁群算法[6]、粒子群算法[7]等。JunMiura在文献[8]中提出了基于SVM的新航路规划方法，基于此，本文提出了SVM在反舰导弹中的应用，同时本方法也适用于其他飞行器。

1 SVM 概述

支持向量机（SVM）是统计学习理论中最年轻的内容，它包括支持向量分类机（SVC）和支持向量回归机（SVR）。其中SVC是基于间隔最大化思想寻找最优超平面的分类方法[9-10]。

给定一组线性可分样本数据集

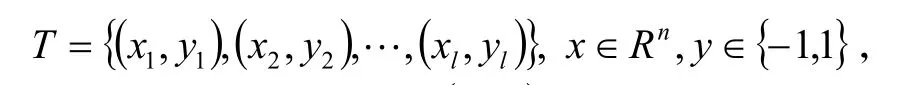
存在惟一的规范超平面(ω⋅x) +b=0，使得下式成立：

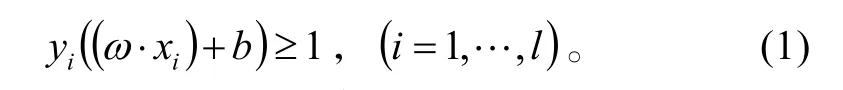
这样通过超平面就使两类样本点落到平面H1:(ω⋅xi) +b=1和 H2:(ω⋅xi) +b=−1的两侧（或H1与H2上）。

而平面H1与平面H2之间的距离为它表示了两类点被分开的程度。SVC就是要在式(1)条件下最大化ρ。求解该问题可以通过求解它的Wolfe对偶问题，即求解下面的二次规划问题：

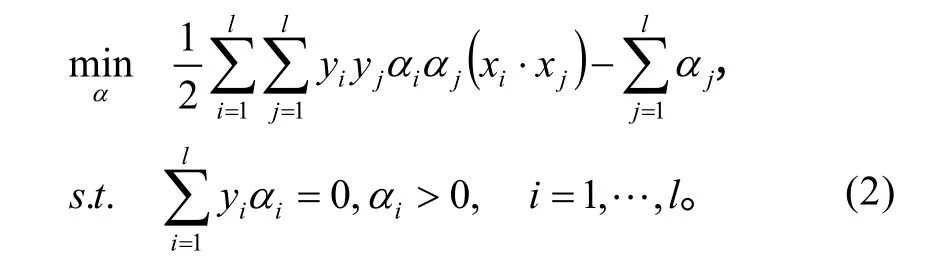
其中与样本点 xi对应的αi满足 αi≠0，则 xi叫支持向量，它在平面H1或H2上，是决定平面的向量。求得 α *后就得到了决策函数 f (x)：

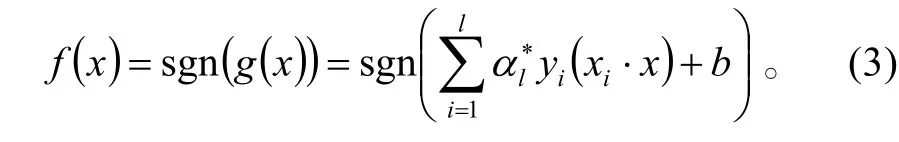
上面是在线性可分的情况下得到的，而很多情况下将是线性不可分划。对于某些线性不可分问题，线性分划造成的错分点可能比较少，这类问题称为近似线性可分。此时我们使用软间隔的办法引入松弛变量iξ 来“软化”约束条件(1)，

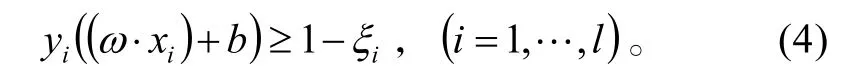
同时在目标函数中引入惩罚参数C，得到如下对偶规划问题：

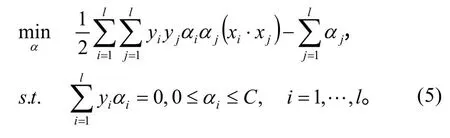
求解结果非零 αi对应了两类支持向量，一是在平面H1和H2上的普通支持向量，此时 0＜αi＜C；另一种为两平面间的边界支持向量，此时 αi=C。

当训练集T的两类样本点集非线性可分时，SVC 通过引进从输入空间X 到另一个高维的Hilbert 空间H的变换 x ↦ϕ(x)，将原输入空间X的训练集转化为Hilbert 空间H的新的训练集：使其在Hilbert 空间H 中线性可分。然后在空间H 中求得超平面(ω⋅ϕ(x))+ b=0，这个超平面可以硬线性分划训练集。采用核函数K 满足

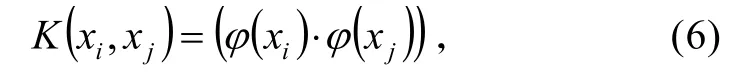
可以避免在高维特征空间进行的复杂运算，解决了“维数灾难”。得到的决策函数为

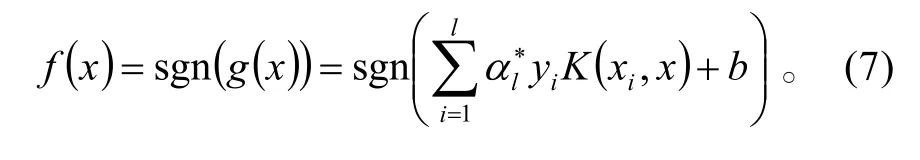
2 SVM 在航迹规划中的研究

引言中已经将反舰导弹的航迹规划问题简化成二维平面的障碍规避问题。此时，航路可以看成障碍中的安全走廊，这条安全走廊将障碍物分成了两部分：一部分在航路的左边；另一部分在航路的右方。因此，我们可以利用SVM 良好的分类能力，将这两部分障碍分开，从而得到分界曲线作为航路。可以看出，要将SVM 应用到航路规划中来，首先，得对规划空间进行划分，将规划空间中的障碍规划成两类[3]；然后，应用SVM的分类能力。本文直接以初始点与目标点的连线为基准线[8]。

2.1 障碍物的划分

假设(x0,y0)为出发点，(xT,yT)为目标点，则基准线方程为：

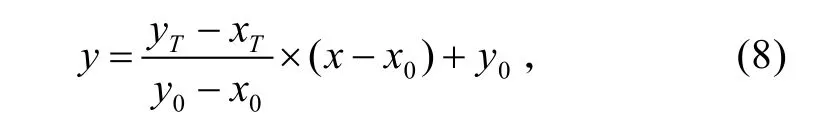
式中：(x,y)为障碍的中心坐标。

根据y的值，规划空间中所有的障碍可以分成以下两类：

正类障碍：y＞0；

负类障碍：y＜0。

若y=0，则根据具体的情况来分析：将它分成正类和负类各一次进行规划，若判别为正类时规划出的航路短，则为正类，反之亦然。在航路规划中，先将不互相覆盖的威胁区域分离开，取它的周围特征点来表示该威胁区域。如果两个障碍区域有重叠现象，则可以将它们看成是一个障碍区域。如图1中，障碍a 和b 重叠，故视为一个障碍。

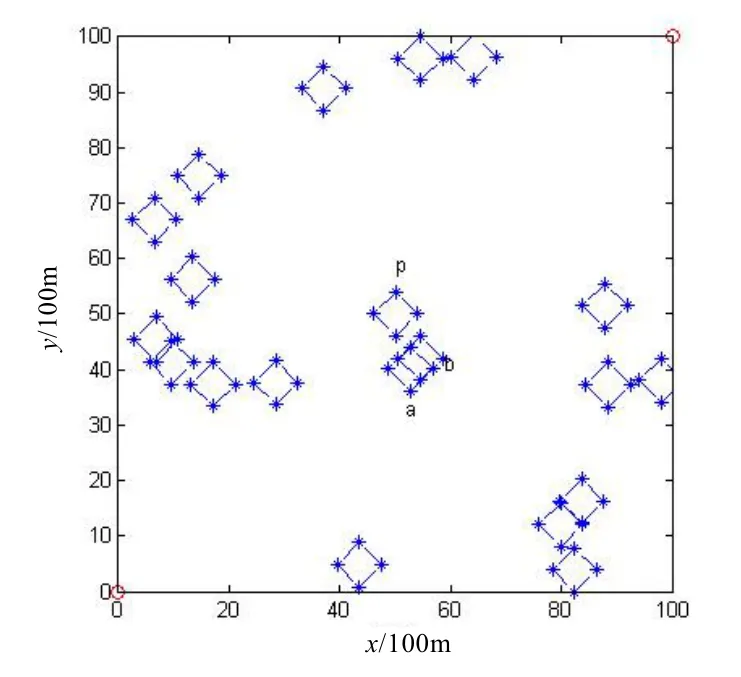
图1 障碍图

2.2 SVM 规划出的航路

利用SVM 对上面的两类障碍物进行规划，得出判别决策函数式(7)。取

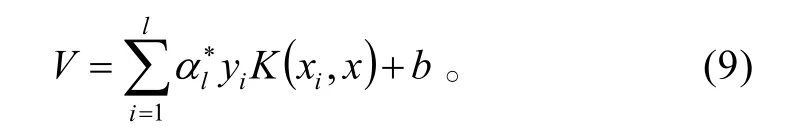
正类障碍区域：V≥1；

负类障碍区域：V≤−1；

安全航路区域（间隔区域）：−1＜V＜1。

我们希望目标点和初始点都落在间隔区域中，这样就可以寻找从出发点到目的点的航路，同时也确保了反舰弹最安全地飞行[8]。

2.3 辅助障碍点的选取

我们知道SVM 规划出的间隔区域有可能是非连通的。为了尽量使出发点和目标点落在同一间隔区域内，我们加入了一些辅助障碍点引导间隔区域经过出发点和目标点。

辅助障碍点的选取：

1）在出发点和目标点附近

为了确保间隔区域经过出发点和目标点，我们在它们两侧分别设了N个正类、负类障碍点，并且平行于标准线，如图2所示。

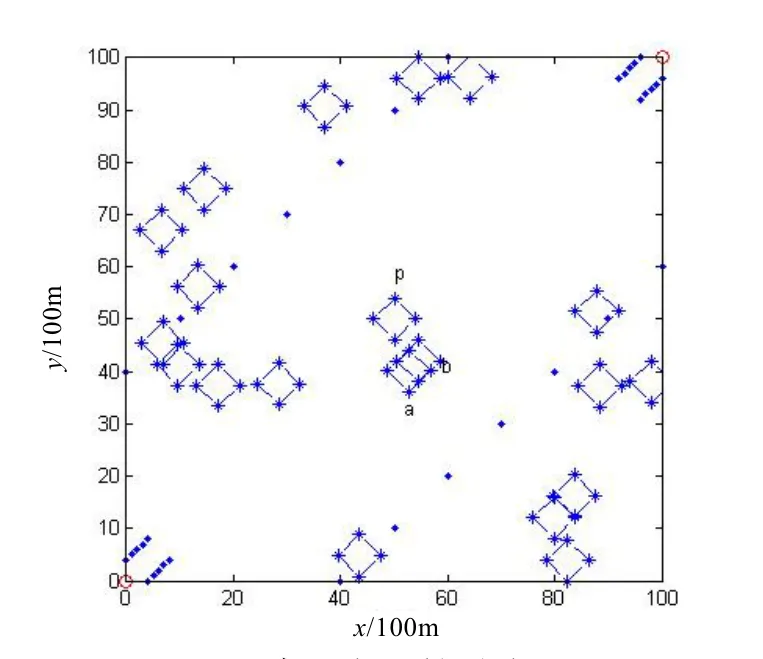
图2 障碍点和辅助点图

2）中间辅助障碍点的选取

辅助障碍点的选取可以引导SVM 作出我们所需要的间隔区域。但是它毕竟是虚设的，所以不能影响实际存在的障碍。所以要以一定的距离平行标准线选取，本文取各类障碍距离标准线的平均距离dE，则两类辅助障碍点的方程为：

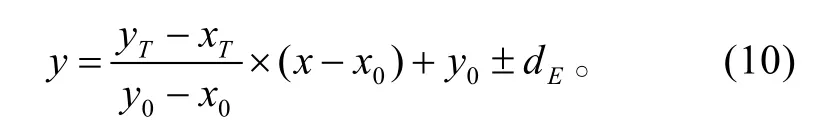
3 仿真验证

在仿真过程中，选取规划的区域是1×100km2正方形区域，设置了20个边长为400×m的正方形障碍，其中正方形障碍P是特别设定的，正好位于出发点和目标点的连线上。其他的是随机生成的障碍。在仿真过程中我们采用了高斯径向基函数

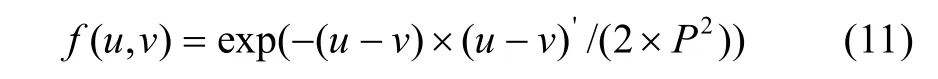
作为SVM的核函数，其中P 选为10，C 选为300。仿真结果如图3所示。

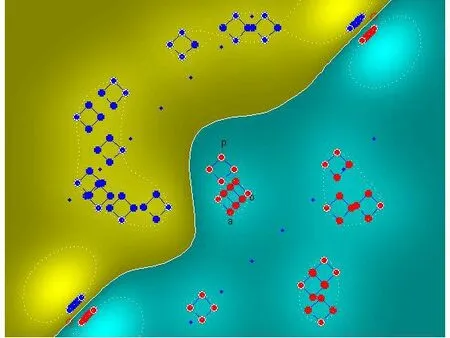
图3 基于SVM的障碍分类图

从而得到实际飞行航迹图如图4所示，此时SVM的支撑向量的个数为50个，占全部向量的41.7%。当P 选为25，C 选为300，此时仿真结果如图5所示，此时SVM的支撑向量的个数为20个，占全部向量的16.7%。

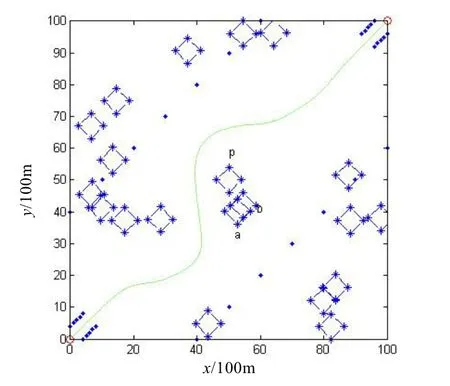
图4 实际飞行航迹图

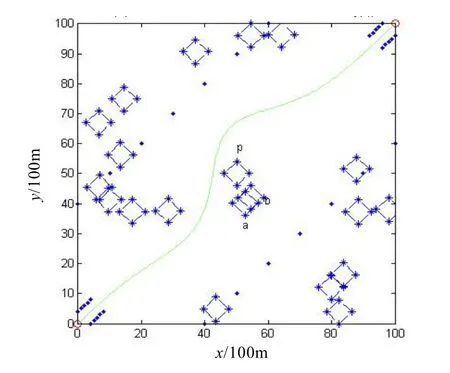
图5 实际飞行航迹图

由图5可以看出SVM 用于航迹规划是可行的，虽然该方法不能保证航迹最短，但是在燃料条件等允许的条件下，它能保证飞行器最安全地在障碍间飞行，并且由SVM 规划出的航迹还不必进行光顺处理。同时，也存在缺陷，就是有关核函数及其参数的选取对结果影响很大。

4 结论及展望

本文研究了SVM 在航路规划中的应用，从仿真结果来看，它是一种有效可行的方法，由它规划出的航迹不必进行光顺处理。但同时，核函数及其参数的选取一直是SVM 问题中的难题，也将成为SVM 在航迹规划中应用的瓶颈。再者，本文仅研究了无威胁的障碍，对于其威胁性是有待进一步研究的问题。

[1]柳长安,李为吉,王和平.基于蚁群算法的无人机航路规划[J].空军工程大学学报:自然科学版,2004,5(2):9-12.

[2]叶文,朱爱红,范洪达.低空突防航路规划算法综述[J].系统仿真学报,2007,19(10):2357-2361.

[3]张雅妮,高金源.一种基于改进A*算法的三维航迹规划方法[J].飞行力学,2008,26(1):48-51.

[4]范晨,王正杰.基于A*算法的飞行器三维航迹规划研究[J].弹箭与制导学报,2006,26(1):650-656.

[5]虞蕾,赵红,赵宗涛.一种基于遗传算法的航迹优化方法[J].西北大学学报:自然科学版,2006,36(2):205-213.

[6]李栋,曹义华,苏媛,等.基于改进蚁群算法的低空突防航迹规划[J].北京航空航天大学学报,2006,32(3):258-262.

[7]陈冬,周德云,冯琦.基于粒子群优化算法的无人机航迹规划[J].弹箭与制导学报,2007,27(4):340-342.

[8]JUN MIURA.Support Vector Path Planning[C]//Proceedings of the 2006 IEEE/RSJ.International Conference on Intelligent Robots and Systems,BJ:IEEE Press,2006:2894-2899.

[9]邓乃扬,田英杰.数据挖掘中的新方法——支持向量机[M].北京:科学出版社,2004.

[10]VAPNIK V N.Statistical Learning Theory[M].John Wiley &Sons,New York,1998.