基于复杂网络理论的Internet拓扑节点特征分析
庄天舒
(长春大学 计算机科学与技术学院,吉林 长春 130022)
0 引言
Internet作为人类社会信息化的标志,虽然由人类亲自创造,但人们对其内在特征尚未充分了解。一个例子就是IP级拓扑,即以转发路径上每跳IP地址为顶点,相邻跳为边的图。复杂网络理论是基于图论和统计物理的一门交叉学科,正是研究网络拓扑的一个有力工具。本文基于复杂网络理论对实际测量的IP级拓扑进行特征分析。
1 复杂网络节点特征
1.1 基本概念
一个网络拓扑可以表示为一幅图G,定义为一个N个顶点(或节点)的集合N(G)和一个M条边(链接)的集合E(G)。每个顶点可以由一个整数值i=1,2,…,N来表示;边表示为一个对(i,j),即顶点i和顶点j相连。G是简单的,不含自环和重边。G可以表示为一个邻接矩阵A,元素aij=1,若(i,j)∈E(G);否则aij=0。顶点i的邻域为n(i),即与i相连的顶点集合。
顶点i的度(degree),ki,是与其相连边的数量,即集合n(i)的势|n(i)|(在物理学文献中,这个量称为“连通性”(connectivity)[2])

1.2 度与相关特征
度是顶点的重要特征[4],基于顶点度,会得到许多网络测度。最简单的是最大度(maximum degree):

一个网络的平均度是网络中所有顶点的ki的平均值

不同顶点度之间的相关性,在许多网络结构和动力学属性中扮演重要角色[5]。最自然的方式是考察一条边所连两个顶点间的相关性。该相关性可由联合度分布P(k,k'),即任意一条边的两端分别是一个度k顶点和一个度k'顶点的概率,来描述。
另一个刻画顶点度之间依赖的方法是一个度k顶点的任意邻居具有度k'的条件概率[6,7],

注意∑k'P(k'|k)=1。对于无向图,P(k,k')=P(k',k)且 k'P(k|k')P(k')=kP(k'|k)P(k)。P(k,k')和P(k|k')形式化地描述顶点度分布,但是难以对之进行实验评价。特别是重尾分布,它是有限网络规模和少量顶点具有高度的结果。为处理此问题,可以计算一个给定度k的顶点最近和(average degree of the nearest neighbors)[8],
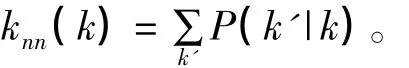
若无相关性,knn(k)独立于k,knn(k)=<k2>/<k>。若knn(k)是k的递增函数,高度顶点趋向于与高度顶点相连,则网络是相配的(assortative),而当knn(k)是k的递减函数时,高度顶点趋向于连接低度顶点,则网络称作非相配的(disassortative)[9]。一个确定度相关性的方法是使用边两端的度的Pearson相关系数[13]:
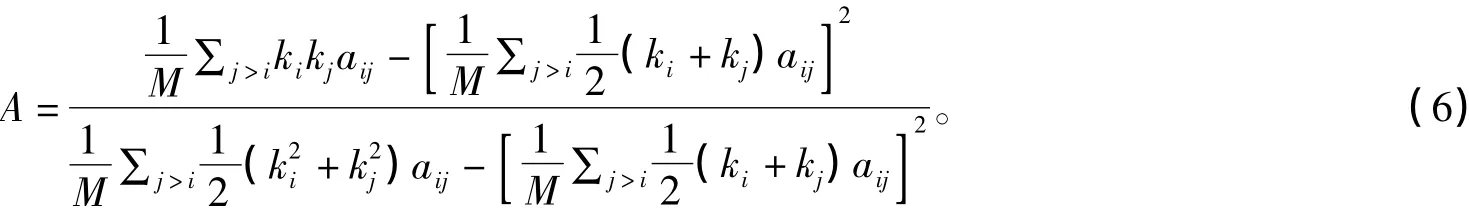
若A>0,则网络是相配的;若A<0,则网络是非相配的;若A=0,则顶点度间不相关.
1.3 聚集系数(Clustering Coefficients)
特征化三阶环出现的方法之一是使用聚集系数(clustering coefficient)。两个不同的聚集系数被频繁使用。首先是传递性(transitivity)[3],其基于如下定义:

这里,NV是网络中三角的数量,N3是连通三元组的数量。因数3是因为每个三角可以看作三个不同的连通三元组,从而保证0≤C≤1。
一个三角是一个彼此相连的三顶点集合;一个连通三元组是连通的三顶点集合,即两个顶点与另一个顶点(中心点)邻接。所以,有
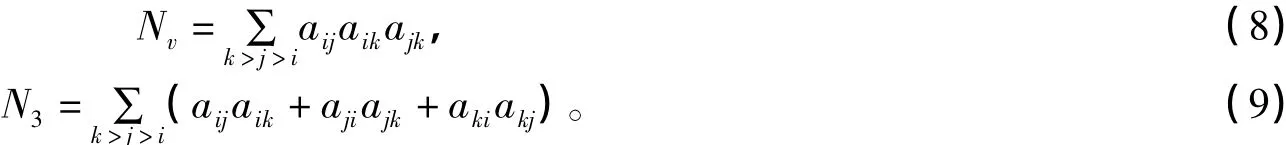
这里,aij是邻接矩阵A中元素,对所有不同顶点i,j和k的三元组只求和一次。
另一个是聚集系数<c>,其中定义一个给定顶点i的聚集系数[1]:

这里,NV(i)是顶点i所在三角数量,N3(i)是以i为中心的三元组数量:

2 拓扑测量实验
截至2004年8月31日,中国IPv4地址空间约为218K个/24前缀,自治域约180个,在Internet中分别约占4%和0.8%。覆盖中国网络的测量实践主要包括:
目前活跃的DIMES项目[11],在当时的测量资源仍然有限,而且志愿主机测量能力远不及专用监测点。例如,就其测得的中国部分而言,只发现了41条边。
CAIDA分布于全球的25个skitter监测点使用相同目标集,目标数约2.20M,落入中国网络的目标约29K。收集21个监测点上一个测量周期的数据,将此图命名为“SKTP”,提取属于中国网络的部分,命名为“SKCN”。
哈尔滨工业大学开发了一个测量工具fastrace,并将其安置于全国12个省会城市的监测点上。对中国IP级网络实施测量,各监测点使用不同目标集,平均目标数为1.28M,无重复目标数达5.03M,获得的图命名为“FTCN”。
提取在2004年12月19~21日间的测量结果,对匿名节点和私有IP地址全部删除而不做推测。将FTCN和SKCN合并拓扑命名为“CNTP”。这四幅拓扑图在本研究中的角色为:SKTP—完整性较低的Internet拓扑;SKCN,FTCN,CNTP—完整性较低,较高,最高的中国拓扑。另外,2005年5月,Zhou等[11]从国内6个监测点测量7.4K个目标,但其目的是发现AS级拓扑,而没有发布IP级拓扑数据。
3 复杂网络特征比较分析
通过计算得到四幅拓扑的特征,列于表1。度分布服从幂律P(k)~k-γ[12]。四幅拓扑的幂律指数γ≈2.3惊人的一致。对于度的最大值,平均值及最小值比例,度分布幂律网络中,max{k}~N1/(γ-1)[10],四幅拓扑的差异说明了这种规模关联性。四幅拓扑都具有略微的非相配性,A<0,即低度顶点倾向与高度顶点相连。
对于平均聚集系数<c>及其替代传递性C。理论上,BA网络中<c>~N-0.75,随机网络中<c>=<k>/N,小世界网络中<c>与<k>相关,可达3/4[10]。从实际情况看,IP级拓扑的<c>并非如BA网络那样绝对与规模相关,也比随机网络中的高,但不及小世界网络的。也就是说,IP级拓扑的<c>是与N和<k>相关,而且略有小世界特征。

表1 所发现拓扑的特征
4 结语
本文提取了实测的Internet的IP级拓扑中蕴含的若干复杂网络特征,证明Internet拓扑节点度服从幂律,具有非相配性,以及小世界网络的高聚集性。
[1]Watts D J,Strogatz S H.Collective dynamics of'small-world'networks[J].Nature,1998,393(6684):440 - 442.
[2]Dorogovtsev S N,Mendes J F F.Evolution of networks[J].Advances in Physics,2002,51:1079 -1187.
[3]Newman M E J.Scientific collaboration networks:I.Network construction and fundamental results[J].Physical Review E,2001,64(01):016131.
[4]Dorogovtsev N,Mendes J F F,The shortest path to complex networks.arXiv:cond-mat/0404593.2004.
[5]Maslov S,Sneppen K.Specificity and stability in topology of protein networks[J].Science,2002,296(5569):910 -913.
[6]Bogu M,Pastor-Satorras R.Epidemic spreading in correlated complex networks[J].Physical Review E,2002,66(04):047104.
[7]Bogu M,Pastor-Satorras R,Vespignani A.Statistical mechanics of complex networks[J].In:Lecture and notes in physics.2003.127.
[8]Pastor-Satorras R,V zquez A,Vespignani A.Dynamical and correlation properties of the Internet[J].Physical Review Letters,2001,87(25):258701.
[9]Newman M E J.Assortative mixing in networks[J].Physical Review Letters,2002,89(20):208701.
[10]Albert R,Barab si A-L.Statistical mechanics of complex networks[J].Reviews of Modern Physics,2002,74(1):47.
[11]Shavitt Y,Shir E.Dimes:Let the internet measure itself[J].SIGCOMM Computer Communication Review,2005,35(5):71 -74.
[12]Faloutsos M,Faloutsos P,Faloutsos C.On power-law relationships of the Internet topology[J].SIGCOMM Computer Communication Review,1999,29(4):251 -262.
[13]Newman M E J.Assortative mixing in networks[J].Physical Review Letters,2002,89(20):208701.

