基于多结构元素的脊骨边缘提取

孙晶莹，王佩宇

(1.长春工程学院 理学院，吉林 长春 130012;2.国家开发银行，北京 100037)

0 引言

图像的边缘对人类的视觉系统具有重要意义，它是人类判别物体的重要依据，是图像的最基本特征之一。边缘中包含着景物有价值的边界信息，这些信息可以用于图像分析、目标识别以及图像滤波，并且通过边缘检测可以极大的降低后继图像分析处理的数据量。所谓边缘是指其周围像素灰度有变化的那些像素的集合。边缘广泛存在于物体与背景之间，物体与物体之间。物体的边缘是由灰度不连续所反映的。图像边缘检测是图像处理中的一项关键技术，边缘检测的实质是采用某种算法来提取出图像中对象与背景间的交界线。

图像边缘检测对于物体识别是非常重要的，得到图像的边缘，能使图像分析大大简化。很多图像并没有具体的物体，对于这些图像的理解取决于它们的纹理性质，而提取这些纹理性质与边缘检测有极其密切的关系。所以边缘检测是数字图像分析处理的前提，检测结果的优劣影响着下一步图像压缩、计算机视觉、模式识别的应用，所以对它的研究具有现实意义和理论意义。

运用数学形态学的基本理论和方法，从结构元素的角度出发，提出了—种多结构元素的选取方案，并采用适当的处理算法进行图像的边界识别，进而达到脊骨图像中边缘信息提取的目的。

1 数学形态学原理

数学形态学是一门建立在严格数学理论基础之上的学科，它的理论基础涉及到微分几何，拓扑学，现代概率论，近世代数与集论，图论等一系列数学分支。另一方面，数学形态学又是一门密切结合实际的学科，它在数字图像处理中有广泛的应用。

数学形态学作为一种用于数字图像处理和识别的新理论和新方法，它的理论很复杂，是“惊人的数学”，但它的基本观念却是简单的和优美的。它最基本的思想是将图像看成是点的集合，用结构元素对其进行移位、交、并等集合运算从而构成了形态学的各种处理算法，作为一种特殊的的数字图像处理方法，数学形态学有其独有的特性。

1.1 二值形态学

数学形态学在二值图像处理中有四种基本变换，包括膨胀、腐蚀、开变换和闭变换。它们是全部形态变换的基础。设A是被研究的图像，B是结构元素，则A被B膨胀的结果可以定义为其中符号Y是集合论中的“并”的记号。A⊕B又称为A与B的Minkowski和。

腐蚀的定义是通过膨胀以及图像反射和集合取补的概念来定义。A被B腐蚀的结果为A⊖B=(Ac⊕c，其中Ac表示A的补或余集，即从整幅图像中去掉A后所剩的部分。上式表明，先求A的补集被B的反射膨胀的结果，再求这一结果的补，最终得到的图像便称为A被B腐蚀的结果，或A与B的Minkowski差。

A被B进行开运算的结果，或者简称为A对B的开，定义为A◦B=(A⊖B)⊕B，即A先被B腐蚀，再被B膨胀的结果。利用开运算可以消除散点和“毛刺”部分。即对图像进行平滑。对于标准零件，可以通过检验毛刺部分的大小来判断它是否合格。

图像A被结构元素B进行闭运算后的结果，或A对B的闭，定义为:A·B(A⊕B)⊖B。因此，执行闭运算的过程与开运算恰好相反:先被B膨胀，再被B腐蚀。

1.2 灰度形态学

实际应用中绝大多数遇到的是灰值图像，如遥感图像，显微图像，照片等。为此，我们引入灰值图的图像代数运算。

定义2.1 设h和k分别为定义在E的子集H和K上的函数，则h被k膨胀后依然是一个函数，记为h⊕k，它由下式定义:

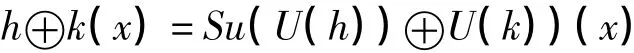
定义2.1 设H和K都是E的子集，且有函数h:H→G，k:K→G，h被k腐蚀仍为函数，记为h⊖k，它按下式定义:

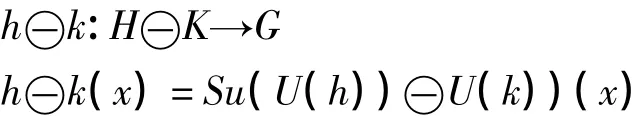
按照定义，计算h⊖k时要先计算h和k的阴影U(h)和U(k)，再计算U(h)和U(k)在二值意义下的腐蚀运算，最后再计算这一结果的表面函数。

与二值图的开变换与闭变换相似，可以用灰值图的腐蚀与膨胀定义灰度图的开变换与闭变换。设函数h，k的定义域都是E的子集，h被k开变换定义为h◦k=(h⊖k)⊕k，

h被k闭变换定义为h◦k=(h⊕k)⊖k

2 多结构元素提取边缘流程

实验数据是一幅脊骨图像，具体提取过程如下:

(1)预处理。首先对原始影像作基于色彩空间的变换，并提取表示亮度信息的波段。然后根据影像灰度直方图对图像进行阈值分割，幅值小于阈值的系数为噪声，给予抑制，而幅值大于阈值的系数给予一定的增益。经过如此处理后，达到了增强图像的目的。结果如图1所示。

(2)多结构运算。大尺度的结构元素有利于去噪和图像中景物轮廓的定位，而小尺度的结构元素有利于保持景物中的小细节，这一步中，结构元素大小的选取决定了脊骨信息的提取尺度。因此先用尺寸较小的矩形结构元素进行膨胀，再使用尺寸较小的圆形结构元素进行开运算，以保持图像中的细节。形态学开运算后，依据脊骨图像自身的几何特征，使用长线状结构元素进一步对形态学膨胀后的结果进行形态腐蚀运算得到脊骨图像边缘，如图2所示。

图1

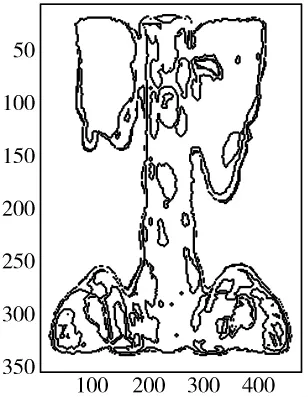
图2

(3)常用边缘算子检测。选用sobel，canny两个常用的边缘检测算子对脊骨图像进行边缘检测，如图3所示。其中(a)为原图，(b)，(c)分别为sobel，canny算子检测结果。

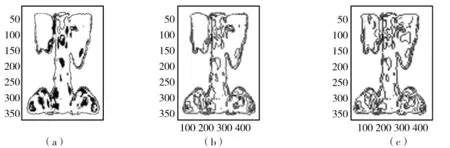
图3

(4)抗噪性。加入椒盐噪声，对图2，图3进行抗噪性实验，实验结果如图4所示。其中图(a)，(b)，(c)分别为sobel，canny算子和多结构元素抗噪性检测结果。

图4

3 实验结果分析

从图中可以看出，用常用的边缘算子提取轮廓包含了很多不重要细节，边缘不连续情况较严重且存在误检，且算子抗噪性较差。而用多结构元素的算法检测边缘，在一定程度上保持图像边缘细节，边缘的连续性及抗干扰能力方面都有所增强。

该算法的优势:用多结构元素的方法可以提取不同大小的边缘，有利于提取细节信息和保持图像整体边缘轮廓，在一定程度上保证了图像信息的完整性，对噪声的图像处理的比较好，对噪声有一定的抑制能力，该方法具有通用性，有较好的适用价值。此外，如何采用恰当的结构元素组合，建立对不同类型的图像进行针对性边缘提取的客观评价算法，这一点既是难点也是一个很有价值的研究方向，有待进一步研究。

［1］Liang Yong.Applications of multi-orientation morphological structure elements in edge detection［J］.J Yunnan University，1999，21(25):392 －394.

［2］岳洪伟，李扬，蔡肯.数学形态学在图像处理中的应用与展望［J］.影像技术，2006(2):19－21.

［3］魏明果.实用小波分析［M］.北京:北京理工大学出版社，2005.

［4］唐常青，吕宏伯，黄铮，等.数学形态学方法及其应用［M］.北京:科学出版社，2005.

［5］贺兴华，周媛媛，王继阳，等.MATLAB7.X图像处理［M］.北京:人民邮电出版社，2006.

［6］任获荣.数学形态学及其应用［D］.西安:西安电子科技大学，2004.

［7］龚炜，石青云，程德民.数字空间中的数学形态学一理论及应用［M］.北京:科学出版社，1997.