卫星和飞船的跟踪测控模型

王 庆，王东强

(苏州职业大学 基础部，江苏 苏州 215104)

1 问题提出

卫星和飞船在国民经济和国防建设中有着重要的作用，对它们的发射和运行过程进行测控是航天系统的一个重要组成部分，理想的状况是对卫星和飞船(特别是载人飞船)进行全程跟踪测控。

测控设备只能观测到所在点切平面以上的空域，且在与地平面夹角3度的范围内测控效果不好，实际上每个测控站的测控范围只考虑与地平面夹角3度以上的空域。在一个卫星或飞船的发射与运行过程中，往往有多个测控站联合完成测控任务，如神舟七号飞船发射和运行过程中测控站的分布。

请利用模型分析卫星或飞船的测控情况，具体问题如下:

(1)在所有测控站都与卫星或飞船的运行轨道共面的情况下，至少应该建立多少个测控站才能对其进行全程跟踪测控?

(2)如果一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角，且在离地面高度为H的球面S上运行。考虑到地球自转时该卫星或飞船在运行过程中相继两圈的经度有一些差异，问至少应该建立多少个测控站才能对该卫星或飞船可能飞行的区域全部覆盖以达到全程跟踪测控的目的?

(3)收集我国一个卫星或飞船的运行资料和发射时测控站点的分布信息，分析这些测控站点对该卫星所能测控的范围。

2 问题分析和模型假设

问题一，假设卫星测控站分布在与卫星轨道共面的地球表面，且卫星的运行轨道为圆。利用几何关系给出全部覆盖需要的测控站点数与卫星高度的关系。当卫星的运行轨道为椭圆，卫星运行轨道的一个焦点在地球中心，利用几何关系给出每个测控站的覆盖范围。问题二，在地球自转的影响下卫星运行过程中星下线的轨迹是地球表面的一些曲线，计算测控站的数量比较困难。一种粗略的估算方法是设置许多测控站，使得其能覆盖卫星飞过的所有空域。计算这个涵盖赤道的球面的立体角，再用一个观测站所能覆盖的立体角去除得到要覆盖这个区域至少需要的观测站。问题三，收集卫星或飞船的发射或运行数据:轨道倾角、高度等;收集该卫星发射和运行过程中观测站的数据:数量、位置等;给出卫星运行轨道、卫星运行过程中的轨迹方程、每个站的测控范围、卫星或飞船在运行到某一圈时可测控的范围，最好能给出一段最长的观测时间。

3 模型的建立和求解

3.1 问题一

在此问题中(见图1)，我们假设卫星测控站分布在与卫星轨道共面的地球表面。

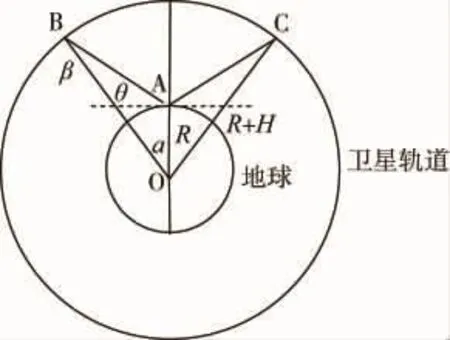
图1 卫星的运行轨道为圆

首先考虑简单情形，卫星的运行轨道为圆。

设卫星或飞船飞行对地高度为H，地球半径为R，卫星的飞行轨道是以地心为圆心R+H为半径的圆。在A处设有一测控站，测控范围边线与地平面的夹角为θ，为确定测控站数应先计算出观测区域在地球表面上投影所对应的圆心角2α。根据图1，在ΔABO中，由从而 2α=故所需的测控站个数n(θ，H)为:

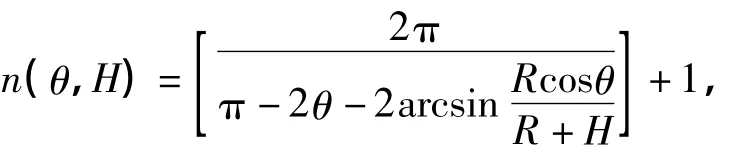
由于在实际中卫星或飞船绕地球运转的轨道是椭圆形的。(见图2)

我们取椭圆轨道上距地心最近的距离为H0，以地心O为圆心，R+H0为半径作圆(图中虚线圆)。由于虚线圆包含在椭圆区域内，若能监控到圆周及其以外空域，则一定能监控到椭圆及以外空域。因此我们只要在地球上均匀建站监控整个虚线圆周。根据上述方法所需的测控站个数为n(θ，H0)。

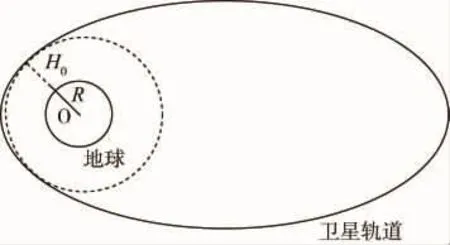
图2 卫星或飞船绕地球运转轨道是椭圆形

3.2 问题二

由于卫星或飞船的运行轨道与地球赤道平面有固定的夹角，而且地球自转时该卫星或飞船在运行过程中相继两圈的经度有一些差异。因此，在地球自转的影响下卫星或飞船运行过程中星下线的轨迹是地球表面的一些曲线。(见图3)

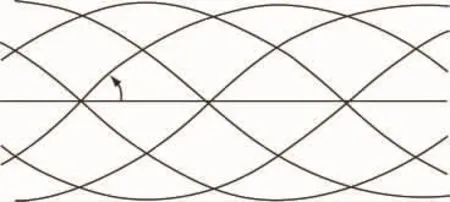
图3 星下线的轨迹是地球表面的一些曲线

由图3观察和分析可以得出:星下点轨迹均匀地分布在赤道的两边，即南纬与北纬之间。因此，只需测控南纬与北纬之间的带状区域内，就可以实现对该卫星的全程测控。

某一观测站的观测区域在以地心为球心，半径为R+H的球面上，其在地球表面的投影为一球冠(见图4)，面积为S=2πR(R－Rcosα)。卫星或飞船运行轨道在地球表面投影的带状区域面积为 S^=4πR2sinλ。若要测控带形区域内所有的范围，需测控站的最少个数为带形区域与球冠面积之比，即

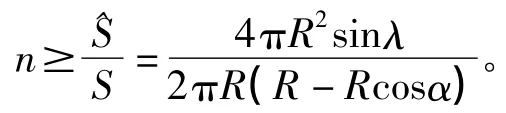
其中，2α表示观测站在距离为H的高空观测区域所对应的圆心角，λ为卫星或飞船的运行轨道与地球赤道平面的夹角。神七轨道平面与地球赤道平面的夹角是42.2度，距地面343km，覆盖这个区域至少需要55个观测站。

3.3 问题三

根据世界地图及神舟七号测控通信系统分布图，我们对其中的测控站进行拟合，发现所成图形近似正弦函数的曲线。对此，我们试作以下分析，飞船的运行轨道在地球表面上的投影应大致服从正弦曲线分布。测控站的作用是为了能够更清晰更准确地了解飞船运行的具体情况，故测控站应分布在飞船的运行轨道在地球表面上的投影曲线上。通过查资料获得神州七号飞船与赤道的夹角为42.2°，高度为343km，周期为90min，小于地球同步轨道运行的高度。由于测控站对飞船的测控范围彼此会有重复，所以很难计算出测控站点对飞船所能测控的范围，由于每一个测控站点在地球上的经、纬度已知，所以我们将由地球经纬网展开成的平面图近似看成是网格图，从而将空间测控范围投影在地球经纬网格图上(见图4)。我们可以通过计算各测控站点测控范围的投影圆能覆盖飞船矩形飞行区域(图4南北纬42.2°之间)的最小覆盖数，求得测控站点对神舟七号飞船所能测控的范围。

我们把飞船矩形飞行区域长k1等分，宽k2等分(不足部分往外延伸)，则整个矩形区域被划分成k1×k2个小正方形区域。经计算

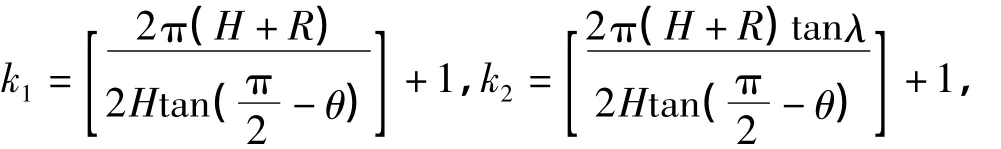
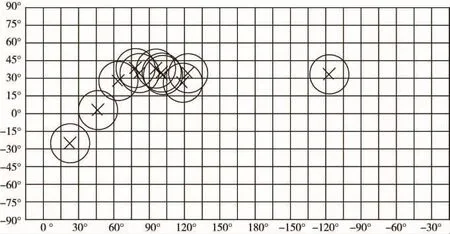
图4 空间测控范围投影在地球经纬网格图

4 结语

对于问题一，我们通过计算观测区域的张角，得到了卫星或飞船的运行轨道为圆形的情况下，对其进行全程跟踪测控的测控站数的计算方法。进一步，把圆形轨道推广到椭圆形轨道。问题二，论证了在地球自转情况下，卫星在地球表面投影为带状区域及观测区域在地球表面的投影为球冠这一事实，并给出了最少测控站点数的计算方法。在问题3中，通过计算各测控站点测控范围的投影圆能覆盖飞船矩形飞行区域的最小覆盖数，求得测控站点对神舟七号飞船所能测控的范围。

［1］中国大学生数学建模竞赛［EB/OL］.www.mcm.edu.cn，2009.

［2］姜启源，谢金星，叶俊.数学模型［M］.3版.北京:高等教育出版社，2003.

［3］柳仲贵.卫星跟踪系统的动态范围［J］.飞行器测控学报，2003，22(1):3.

［4］韩中庚.数学建模竞赛——获奖论文精选与点评［M］.北京:科学出版社，2007.