Alexander与HOMFLY多项式在纽结中的应用

邱海燕，陈震霆

(空军航空大学 数学教研室，吉林 长春 130022)

0 引言

纽结［1］(knot)是三维中的简单闭曲线，即连通的(连成一体)、封闭的(没有端点的)、不自交的(自己与自己不相交，即没有粘连的)曲线。链环［2］可以在空间中自由地连续变形，但是不允许剪断，不许粘合，而变成另一个链环，则这两个链环是合痕的(isotopy)。

纽结理论中我们关心的问题是任意的两个纽结或链环怎样识别他们是否相同，怎样判断它们是否是非平凡的。又因为对于同一个纽结或链环的所有投影图都是合痕的，因此纽结理论的基本问题就成为:任给两个纽结或链环的投影图，它们是否是合痕的，怎样判断它们是否等价于平凡纽结或链环的投影图。我们可以利用合痕不变量来区分。文章主要介绍两种合痕不变量——Alexander［3］多项式和HOMFLY［4］多项式的联系。

1 Alexander多项式与HOMFLY多项式在分离链环上的应用

定理1:若L是有向分离链环，设可分离为两个链环L1，L2，则

(1)Δ(L)=0，

(2)P(L)=P(L1∪L2)= － (l+l－1)m－1P(L1)P(L2)。

则 Δ(L+) －Δ(L－)+(t1/2－t－1/2)Δ(L0)=0。

又 Δ(L+)=Δ(L－)，故 Δ(L)=0。

(2)对L2的交叉指标C(L2)用数学归纳法。

①当C(L2)=0时，即L2为○，则P(L2)=1。

我们知:P(L1∪L2)= － (l+l－1)m－1P(L1)= － (l+l－1)m－1P(L1)P(L2)。

②假设C(L2)＜n时，命题成立。

由于HOMFLY多项式是合痕不变量，同一个链环对其任意投影图计算得到的HOMFLY多项式都相同，故链环L2取其交叉点最少的投影图没有影响。

当C(L2)=n时，设L2的投影图有n个交叉点，则选取某一个交叉点后构造L+，L－，L0(如图1)，并且 L+即为 L1∪L2。

图1 链环示意图

2 Alexander多项式与HOMFLY多项式之间的联系

Alexander多项式是最早被发现的多项式，它只有一个变量t，而HOMFLY多项式中包含两个变量l和m，它们都是有向链环的多项式。下面的定理给出了两者之间的联系。

定理2 将链环L的HOMFLY多项式P(L)中的每个l用i取代，每个m用i(t1/2－t－1/2)取代，则得到该链环的Alexander多项式Δ(L)。

证明:由于HOMFLY多项式与Alexander多项式有类似的法则，只是系数不同，若对法则成立，则得证。

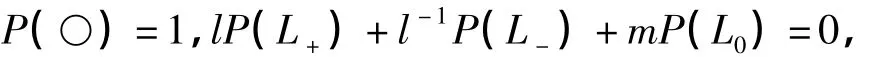
将 l=i，m=i(t1/2－t－1/2)代入得

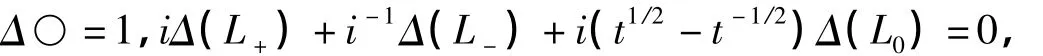
故将链环L的HOMFLY多项式P(L)中的每个l用i取代，每个m用i(t1/2－t－1/2)取代，则得到该链环的Alexander多项Δ(L)。证毕。

HOMFLY多项式是二元多项式不变量，包含Alexander多项式为特殊情况，鉴别力比它更强，更具有普遍性。

3 结语

现在若要计算某个链环的HOMFLY多项式，已经有人编写了一个计算机程序，若利用本文的思想可以进一步简化计算过程，提高运算速度。为了更好地研究纽结提供了有力的帮助。

［1］姜伯驹.绳圈的数学［M］.长沙:湖南教育出版社，1991.

［2］Rolfsen.Knots and links［M］.Berkeley:Pubilish or Perish Press，1976.

［3］Alexander.Topological invariants of knots and links［J］.Trans.Amer.Math.Soc.，1982，30:275 － 306.

［4］Kauffman.New invariants in the theory of knots［J］.Amer.Math.Monthly，1988，95(3):95 －142.

［5］韩友发，胡晓跃，常乐.纽结多项式的性质［J］.吉林师范大学学报:自然科学版，2008，29(2):1－4.