磁通切换永磁电机的空间矢量脉宽调制控制

朱瑛， 程明， 花为， 贾红云

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

传统永磁电机都将永磁体置于转子，为了防止高速运行时磁钢受到离心力的影响而被甩落，转子上都装有不锈钢或非金属纤维材料制成的固定装置。但这样会引起散热困难，而温升最终会导致永磁体发生不可逆退磁，限制电机出力，减小功率密度等。磁通切换永磁（flux-switching permanent magnet，FSPM）电机是一种新型结构的定子永磁型双凸极电机，它克服了传统转子型永磁电机的诸多缺点，具有较好的应用前景［1－3］。

电压空间矢量脉宽调制（space vector pulsewidth modulation，SVPWM）是上世纪80年代后期针对电压源型逆变器所提出的一种控制策略［4］，其控制力图使电机获得幅值恒定的圆形磁场，将电机和控制器作为一个整体考虑，能得到较高的控制性能，因此在高性能电机调速系统中得到越来越多的应用［5－6］。

本文以一台定子12槽/转子10极（12/10极）FSPM电机作为控制对象［3］，其转子和开关磁阻电机相似，定子采用集中绕组，绕组端部较小，节省用铜量并减小铜耗。每4个线圈串联或并联成一相绕组。定子有12个“U”形导磁铁心，中间嵌入12片切向交替充磁的永磁体。与传统的转子永磁型电机相比，定子永磁型电机更便于冷却，在环境温度较高的航天和电动汽车等领域比较适合应用。目前国内外针对该种电机主要采用电流滞环比较的矢量控制策略［7］，本文在理论分析基础上，应用Matlab/SIMULINK构建了基于SVPWM的FSPM电机控制系统仿真模型，并通过仿真及实验对所提出的控制方法的有效性进行验证。

1 数学模型

三相FSPM电机结构如图1所示，其在定子坐标系下的数学模型［7］为

式中:ua、ub、uc为三相相电压;ia、ib、ic为三相电流;Rph为每相绕组电阻;L0为自感的基波直流分量;M0为互感的基波直流分量;ψa、ψb、ψc为三相相绕组匝链的总磁链;ema、emb、emc为三相反电势;Pem为电磁功率;Tpm为永磁磁链与电枢电流作用产生的永磁转矩;Tr为磁阻转矩;Tcog为定位力矩。

FSPM电机的反电势和电流都是正弦波形，所以其模型和正弦波永磁同步电机的d-q轴模型类似。因此忽略电动机铁心的饱和，不计电动机中的涡流和磁滞损耗，假设电动机电流为对称的三相正弦波电流，则经过派克变换后的三相FSPM电机模型为

式中:ud、uq分别为直轴和交轴电压;ψd为d轴绕组中的总磁链;ψq为q轴绕组的总磁链;ωe为电机旋转速度。

id=0的控制方式是一种最简单的控制方法，可以防止电枢反应的去磁作用。此时，式（4）可简化为

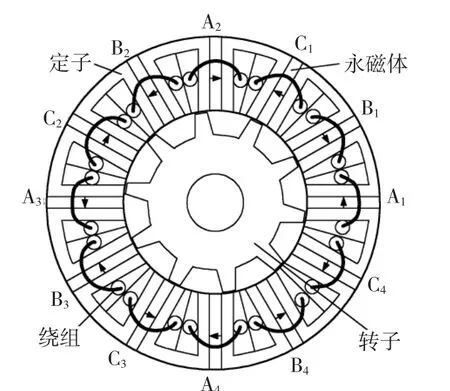
图1 12/10极FSPM电机截面图Fig.1 Sectional view of 12/10 pole FSPM motor

2 基于SIMULINK的FSPM系统建模

在Matlab7.0环境下，利用丰富的模块库，根据FSPM电机数学模型，建立其基于SVPWM的矢量控制系统模型，控制系统的实现框图如图2所示

图2 FSPM电机控制系统图Fig.2 Control system of FSPM motor

2.1 FSPM电机模块

在控制系统的仿真中，FSPM电机模块是核心部分，可分为电机本体模块和转矩测量模块。与简化的电压方程模型不同，三相FSPM电机定子电压方程模型考虑了不同相绕组之间的互感，即每相绕组的电压方程除了与本相电流相关，还与其他两相耦合在一起。由FSPM电机的转矩公式可知，电磁转矩可由3个分量组成:永磁转矩Tpm、磁阻转矩Tr和定位力矩Tcog，因此转矩计算子模型中也有3个部分。

图3是由2个子模块组合后的FSPM电机模块，其中A+、B+、C+为三相绕组与变换器主电路相连的三端口，端口Net为与分裂电容中点相连的三相绕组公共端，端口theta为转子位置角，它由给定转速与时间乘积得到，端口n为给定转速。

图3 三相FSPM电机仿真模型Fig.3 Simulation model of threephase FSPM motor

2.2 电流和速度PI控制器模块

实际应用中，永磁同步电机控制系统中的电流环和速度环大多采用 PI调节器，而本文研究的FSPM电机与PMSM数学模型和控制系统相近，因此也设计了PI调节器模块，电流环PI调节器模块如图4所示，而速度环调节器原理与其相同。

图4 PI调节器仿真图Fig.4 Simulation model of PI regulator

2.3 坐标变换模块

由三相电流 ia、ib、ic变换到两相静止 iα、iβ，为

根据式（6）、式（7），直接使用 SIMULINK/Library Browser中的简单加法、乘法、常量以及输入输

由两相静止坐标系 iα、iβ到旋转坐标系 id、iq，为出模块就可以建立2个坐标变换的模块。

2.4SVPWM生成模块

2.4.1 SVPWM基本原理

电压空间矢量脉宽调制以三相对称正弦波电压供电时交流电动机产生的理想圆形磁链轨迹为基准，用逆变器不同的开关模式产生的实际磁通去逼近基准磁链圆，从而达到较高的控制性能。

电机的理想供电电压为三相对称正弦，设U为线电压，则相电压为

由式（10）可以看出，合成电压矢量是一个随时间变化幅值一定的圆形矢量，而磁链是电压的积分，因此产生的磁场是圆形旋转的，而电机旋转磁场的轨迹问题就可以转化为电压空间矢量的运动轨迹问题。

三相电压源型逆变器由6个功率开关器件组成，基本结构如图5所示。逆变器的上桥臂和下桥臂开关状态互补，因此可以用3个上桥臂的功率器件的开关状态来描述逆变器的工作状态。记功率器件开通状态为1，关断状态为0，a、b、c三相状态分别用 x，y，z表示，则上桥臂 VT1，VT2，VT3的开关状态有8 种组合，可分别表示为［0 0 0］、［0 0 1］、［0 1 0］、［0 1 1］、［1 0 0］、［1 0 1］、［1 1 0］、［1 1 1］。对应的8种电压矢量分别记为U0（000）、U1（001）、U2（010）、U3（011）、U4（100），U5（101），U6（110），U7（111），称为基本空间电压矢量，其中U0、U7为零矢量。

图5 三相逆变器和FSPM电机连接图Fig.5 Connection of inverter and FSPM motor

由此，可以推导出三相逆变器输出的相电压矢量与开关状态矢量的关系为

8个电压矢量的定义如图6所示，使相邻矢量仅变换1位，空间区域可分为6个象限，每象限间隔60°，得到每个扇区的调制波形。合成电压矢量Uref在哪个扇区，就由该扇区的2个相邻电压矢量分别作用一定时间合成得到。

图6SVPWM矢量，扇区和波形Fig.6 Vectors，sectors and waveforms of SVPWM

2.4.2 SVPWM实现算法

1）判断参考电压矢量Uref所在扇区设

定义3 个变量 g、h、k，使得:如果 Ua>0，则 g=1，否则g=0;如果Ub>0，则h=1，否则h=0;如果Uc>0，则k=1，否则k=0。则扇区号N=g+2h+4k。

2）确定相邻2个矢量的作用时间

假设α、β轴的电压分量Uα、Uβ的合成矢量Uref在第Ⅲ扇区，则式中:T为PWM周期;T4为空间矢量U4的作用时间;T6为空间矢量U6的作用时间。根据式（13）和图6可得

每个空间矢量的幅值均为2Udc/3，将其代入式（14），得

同理，可以得到Uref在其它扇区时，相邻空间矢量的作用时间。定义变量x、y、z为

对应第Ⅲ扇区空间矢量的作用时间可表示为T4=－z，T6=x。各个扇区空间矢量作用时间的对应关系如表1所示。

表1 不同扇区的T1、T2取值Table 1 Value of T1、T2in different sectors

根据表1对T1、T2进行赋值，然后对其进行饱和判断:若T1+T2≤T，则保持原值不变;若T1+T2>T，则修正为

3）导通切换时间计算

得到导通时间T1和T2后，可计算出 a、b、c三相功率器件的导通时间为

根据不同的扇区，按照表2对三相功率器件的导通时刻进行赋值，其中Tcm1、Tcm2、Tcm3分别表示逆变器三相桥臂功率器件的导通切换时间。

表2 不同扇区的导通切换时间Table 2 Value of Tcmin different sectors

2.4.3 SVPWM的仿真实现

利用Matlab/SIMULINK中的标准模块，可以建立SVPWM的仿真模型。SVPWM仿真模型可分为扇区判断模块，x、y、z计算模块，T1、T2赋值模块，饱和判断模块，导通时刻计算模块，导通时刻赋值模块及PWM波生成模块。仿真得到的扇区波形和三相调制波波形如图7～图10所示。

图7PWM波生成仿真图Fig.7 Model of producing PWM waveform

图8SVPWM模块仿真图Fig.8 Simulation model of SVPWM

图9 扇区波形Fig.9 Waveform of sectors

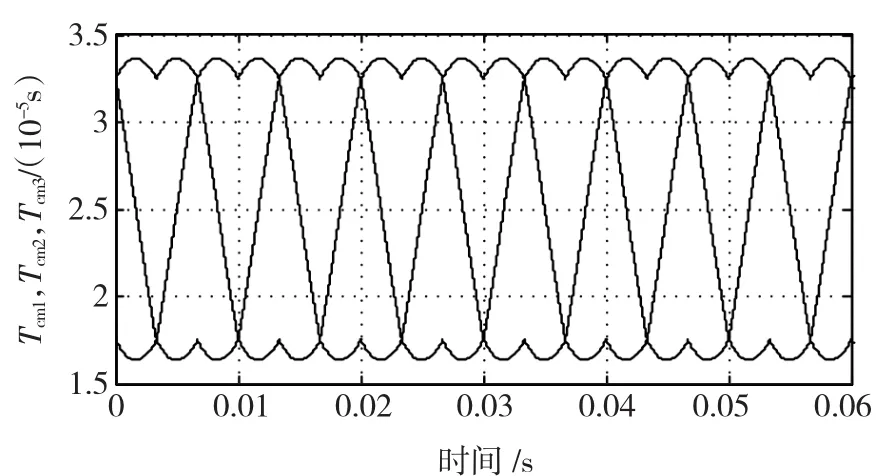
图10 三相调制波波形Fig.10 Waveform of threephase modulation wave

3 FSPM电机系统仿真及实验结果

FSPM实验样机的参数为:定子齿数12;转子极数10;定子外径128 mm;定子内径70.4 mm;气隙长度0.35 mm;有效轴长75 mm;转子内径22 mm;每相绕组匝数70;额定电流3.8 A;额定转矩13 N·m;每相电阻 1.436 Ω;永磁磁链 0.166 Wb;d轴电感14.308 mH;q轴电感15.533 mH;摩擦系数0.8×10－3N·m·s。

仿真参数为:功率器件的开关频率10 kHz;转速300 r/min;负载在起动一段时间后，从3 N·m突变到8 N·m再回到3 N·m，其动态过程仿真结果如图11～图14所示。

图11 FSPM电机转速波形Fig.11 Waveform of motor speed

图12 FSPM电机三相电流波形Fig.12 Waveform of three－phase currents

图 13 id、iq波形Fig.13 Waveform of idand iq

图14 FSPM电机转矩波形Fig.14 Waveform of motor torque

实验主控器采用dSPACE DS1104控制板，逆变器采用智能功率模块PM75RSE120，实验参数设置与仿真时一致，实验过程中使负载突变2次，用示波器测得稳态和负载突变实验波形如图15～图17所示。

图15 稳态三相电流波形Fig.15 Waveform of steady state currents

图16 负载突变转速n及id、iq波形Fig.16 Waveform of id、iqand speedn when the load is changed

图17 负载突变一相电流波形Fig.17 Waveform of current when the load is changed

由仿真和实验波形可知，稳态时FSPM电机转速平稳，转矩脉动小，三相电流谐波也较小，而当负载发生变化时转速和电流都能较迅速得切换并稳定，从而验证了SVPWM控制策略的有效性。

4 结语

磁通切换型永磁电机具有转子结构简单，适合高速运行，冷却方便，功率密度大等优点。本文采用SVPWM的控制方式，建立了基于Matlab/SIMULINK的磁通切换型永磁电机控制系统。仿真和实验结果验证了空间矢量脉宽调制能够应用于磁通切换型永磁电机，为磁通切换型永磁电机系统设计和调试提供了参考。

［1］ HOANG E，BENAHMED A H，LUCIDARME J.Switching flux permanent magnet polyphased synchronous machines［C］//7th European Conference on Power Electronic and Applications，September 8－10，1997，Trondheim，Norway.1997，3:903－908.

［2］ ZHU Z Q，PANG Y，HOWE D，et al.Analysis of electromagnetic performance of flux-switching permanent magnet machines by nonlinear adaptive lumped parameter magnetic circuit model［J］.IEEE Transactions on Magnetics，2005，41（11）:4277 －4287.

［3］ 花为，程明，ZHU Z Q，等.新型磁通切换型双凸极永磁电机的静态特性研究［J］.中国电机工程学报，2006，26（13）:129－134.

HUA Wei，CHENG Ming，ZHU Z Q，et al.Study on static characteristics of novel flux-switching doubly-salient PM machine［J］.Proceedings of the CSEE，2006，26（13）:129－134.

［4］ VAN DER BROECK H W，SKUDELNY H C，STANKE G V.A-nalysis and realization of a pulsewidth modulator based on voltage space vectors［J］.IEEE Transactions on Industry Applications，1988，24（1）:142－150.

［5］ 张春喜，廖文建，王佳子.异步电机SVPWM矢量控制仿真分析［J］. 电机与控制学报，2008，12（2）:160－163，168.

ZHANG Chunxi，LIAO Wenjian，WANG Jiazi.Simulation analysis in SVPWM vector control for a synchronous motor［J］.Electric Machines and Control，2008，12（2）:160 －163，168.

［6］ 王妍，杜军红，陶伟宜，等.基于DSP的空间电压矢量法PWM的研究［J］. 电机与控制学报，2000，4（2）:98－101，105.

WANG Yan，DU Junhong，TAO Weiyi，et al.Study of SVPWM based on DSP［J］.Electric Machines and Control，2000，4（2）:98－101，105.

［7］ 陆炜，程明，花为.新型两相磁通切换型永磁电机调速系统建模与仿真研究［J］.微电机，2007，40（7）:1－6.

LU Wei，CHENG Ming，HUA Wei.Modeling and simulation of novel 2-phase flux-switching permanent magnet motor drives［J］.Micromotors Servo Technique，2007，40（7）:1－6.

（编辑:张诗阁）