导弹三维制导控制一体化设计

尹永鑫， 杨明， 王子才

（1.中国航天空气动力技术研究院第十一总体设计部，北京 100074;

2.哈尔滨工业大学航天学院，黑龙江哈尔滨 150001）

0 引言

导弹制导控制系统的常规设计思路是首先将纵向通道与侧向通道分解，制导回路与控制回路分解，然后分别对它们进行设计。然而，当导弹需要进行快速、大角度机动时，纵向通道与侧向通道之间存在着运动耦合，而且制导回路与控制回路并不互相独立。因此，基于上述思路设计的制导控制系统不能保证导弹的命中精确度［1－4］。此外，为了获得最佳攻击效果，要求导弹在命中目标的瞬间保持期望的姿态［5－6］，这一要求也是常规设计方法难以实现的。因此，对导弹三维制导控制一体化设计方法的研究是十分必要的。

自文献［7］提出制导控制一体化设计的概念以来，经国内外学者的不懈努力，目前制导控制一体化设计已经取得了一定的成果，但仍存在着诸多待解决的问题，例如未摆脱制导回路和控制回路分开设计的框架，未考虑三维制导控制一体化设计问题，即未考虑纵向通道和侧向通道之间的耦合等。

本文对导弹进行三维制导控制一体化设计。首先建立导弹三维制导控制一体化模型，然后给出基于微分几何和特征结构配置的导弹三维制导控制一体化设计方法，并通过仿真来验证该方法的有效性。

1 导弹三维制导控制一体化模型

1.1 弹－目三维相对运动关系

导弹与目标之间的三维相对运动关系如图1所示。其中:M为导弹;T为目标;R为弹－目相对距离;λ为弹－目视线高低角;μ为弹－目视线方位角;Oxsyszs为视线坐标系。

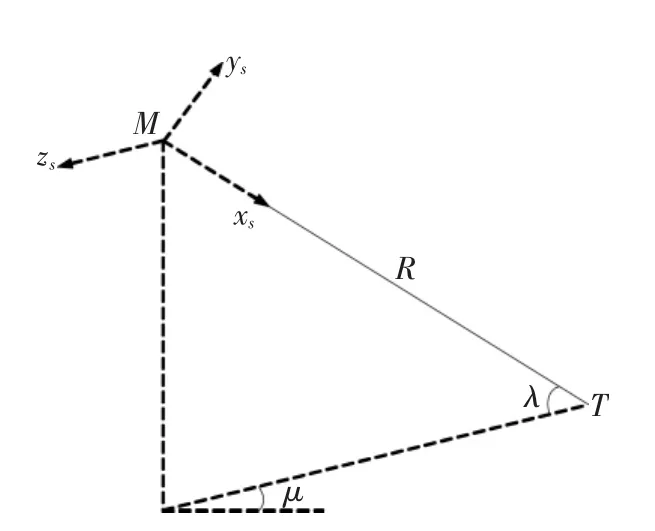
图1 弹－目三维相对运动关系Fig.1 Missile-target 3-D relative geometry relation

结合图1，可以得到视线坐标系相对于惯性坐标系的转动角速度为

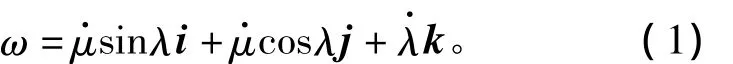
其中，i、j、k为视线坐标系三轴的单位矢量。

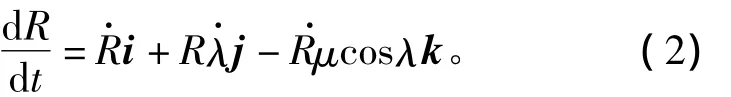
结合式（1）和式（2），可以得到弹－目相对加速度为

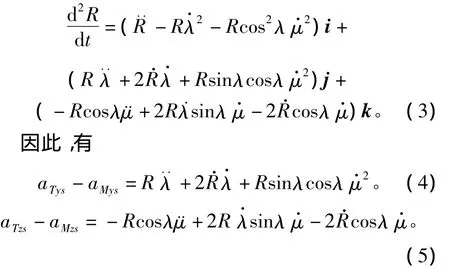
由式（1）可知弹－目相对速度为

其中:aMys、aMzs分别为导弹机动加速度的分量;aTys、aTzs分别为目标机动加速度的分量。

式（4）、式（5）即为球坐标系下的弹－目三维相对运动模型。显然，视线高低角λ和视线方位角μ之间存在耦合。但在常规的设计思路中，纵向平面内的弹－目相对运动关系为

对于制导系统而言，目标的机动加速度为未知量，可以视为系统的不确定性，而导弹的机动加速度可以表示为

1.2 导弹弹体运动模型

考虑导弹在侧滑角β=0、滚转角γ=0时的纵向运动，有关系

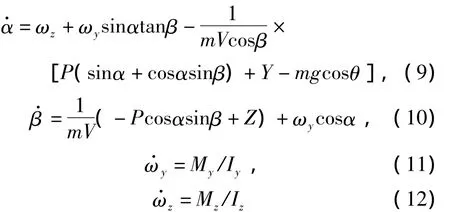
成立。其中，Y、Z、My、Mz分别为升力、侧力、偏航力矩、俯仰力矩，其表达式为

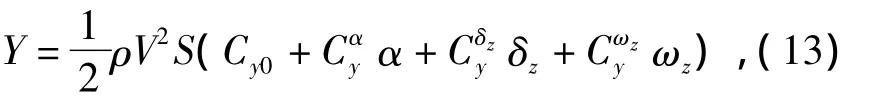
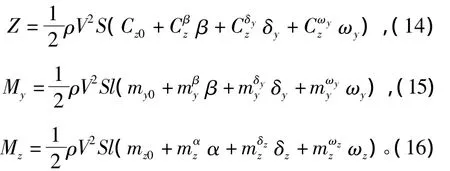
1.3 三维制导控制一体化模型

为了使得导弹在命中目标的瞬间保持期望的姿态，这里取状态变量x=［λ － λdμα β ωyωz］T，控制量 u=［δyδz］T，输出量 y=［λ μ］T。结合式（4）、式（5）和式（7）～式（16），可以得到导弹三维制导控制一体化模型为

由式（18）～式（25）可知，式（17）是一个非线性耦合系统，并且系统阶次大于控制量阶次，直接针对该系统模型进行设计是十分困难的。为此，基于反馈线性化和特征结构配置了导弹三维制导控制一体化设计方法。

2 导弹三维制导控制一体化设计

微分几何方法主要用于消除系统的非线性因素以及实现多变量非线性系统的解耦控制，它在线性化过程中没有忽略掉任何高阶非线性项，因此与基于小扰动原理的线性化方法相比具有更大的优势［8－9］。而特征结构配置方法能够保证系统具有希望的特征值和重数，并能够给出极点配置问题的一切解［10－11］。因此，本文使用微分几何和特征结构配置方法对导弹进行三维制导控制一体化设计。

2.1 三维制导控制系统的反馈线性化

对系统输出方程y=H（x）进行依次微分运算，可得

由于G1（X）非奇异，因此反馈控制量u存在，式（32）即为导弹三维制导控制系统的状态反馈控制量，进一步可以基于特征结构配置的方法进行制导控制一体化设计。

2.2 三维制导控制控制系统的特征结构配置

针对导弹三维制导控制一体化模型，基于微分几何方法得到的线性系统为

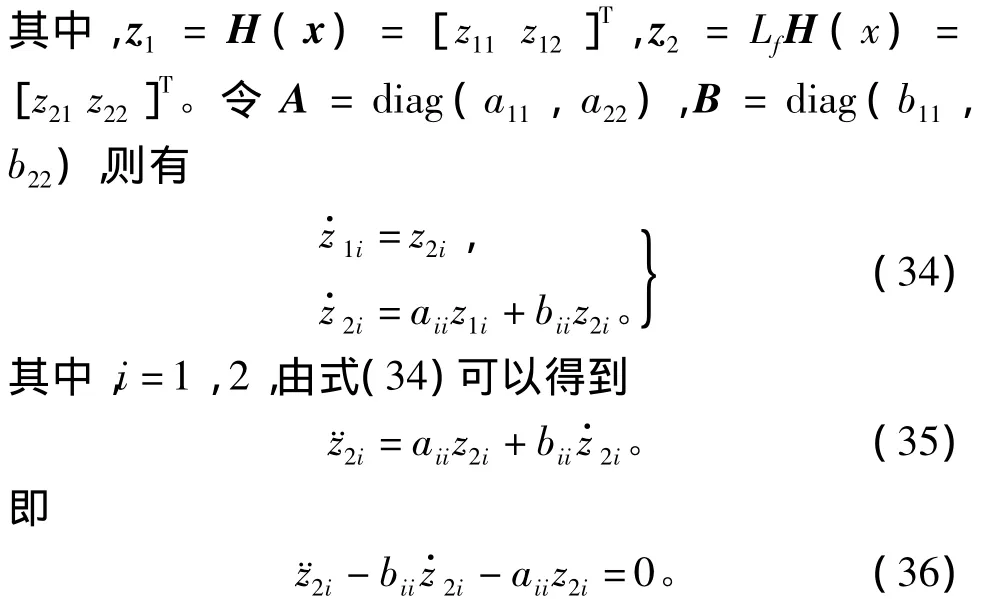
显然，得到式（36）后便可以对其进行特征结构配置，其中aii、bii可以根据系统的期望性能来选取。

3 仿真验证

设仿真算例1参数为视线高低角λ0=45°;视线方位角 μ0=1.79°;导弹攻角 α0=1.5°;导弹侧滑角 β0=0°;导弹位置（xm0，ym0，zm0）=（0，3000，0）;导弹速度（vxm0，vym0，vzm0）=（200，0，250）;目标位置（xt0，yt0，zt0）=（2400，0，3200）;目标速度（vxt0，vyt0，vzt0）=（15，0，20）;目标加速度（axt0，ayt0，azt0）=（1，0，1）。利用本文给出的一体化方法进行三维制导控制仿真实验，导弹与目标的运动轨迹、导弹攻角、导弹侧滑角、弹－目视线高低角、弹－目视线方位角如图2～图6所示，仿真结果如表1所示。

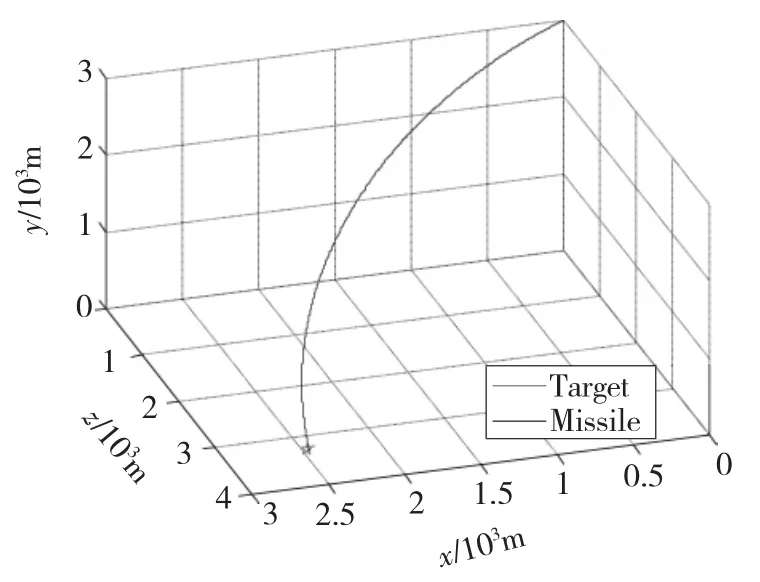
图2 导弹与目标的运动轨迹Fig.2 Trajectory of missile and target

为了进一步考察该方法对机动目标的鲁棒性，取仿真算例2:目标速度（25，0，10）m/s、目标加速度（0，0，－1）m/s2;仿真算例 3:目标速度（20，0，10）m/s、目标加速度（sint，0，cost）m/s2，其它条件均与仿真算例1相同，受到篇幅的限制这里仅给出脱靶量、导弹弹道倾角和导弹弹道偏角，如表2所示。

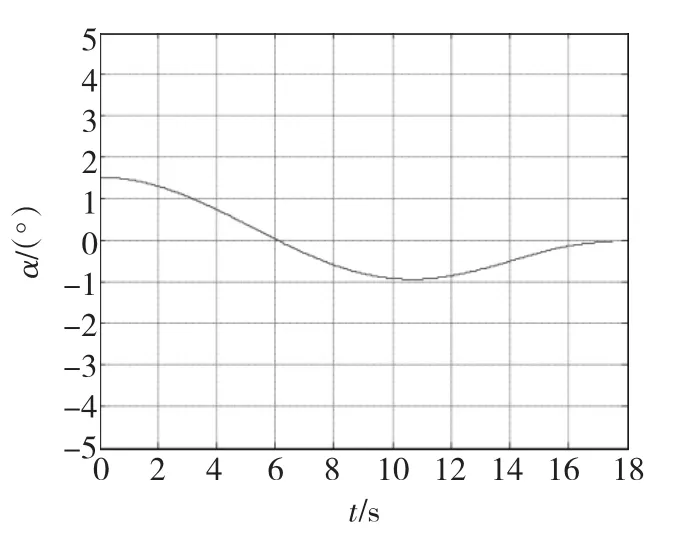
图3 导弹攻角的变化曲线Fig.3 Attack angle of missile

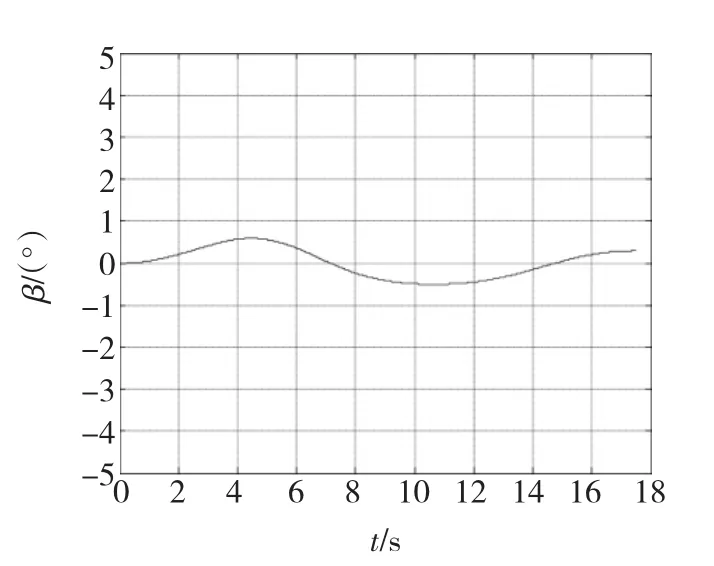
图4 导弹侧滑角的变化曲线Fig.4 Sideslip angle of missile

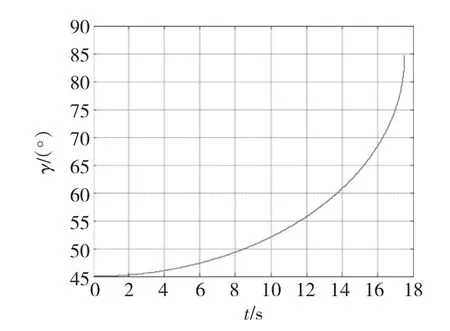
图5 弹－目视线高低角的变化曲线Fig.5 Missile-target lengthways angle of line of sight

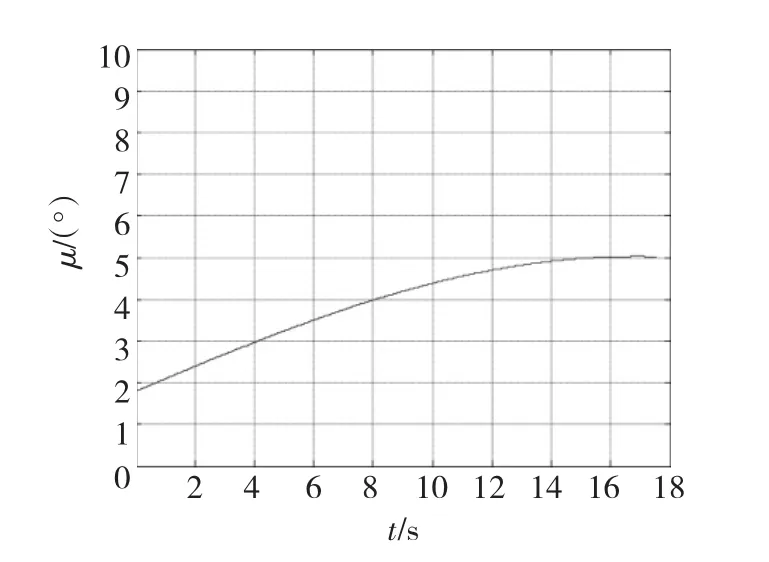
图6 弹－目视线方位角的变化曲线Fig.6 Missile-target azimuth angle of line of sight

由图2～图6和表2可知，在目标进行机动的情况下，脱靶量为0.405 4 m、0.430 6 m、0.493 1 m，导弹的弹道倾角为 84.51°、83.68°、84.09°，导弹的弹道偏角为 5.03°、3.95°、4.19°，因此可以认为导弹都能够垂直命中目标。可见，该方法能够在命中目标的同时保证导弹具有期望的弹道倾角和弹道偏角，而且对机动目标具有较强的鲁棒性和适应能力，从而证明了本文给出的基于微分几何和特征结构配置的导弹三维制导控制一体化设计方法的有效性。

表1 仿真结果Table 1 Results of simulation

4 结语

本文研究了导弹的三维制导控制一体化设计问题。首先建立了弹－目三维相对运动关系，在此基础上结合弹体运动模型给出了导弹三维制导控制一体化模型。为了保证制导控制精度并满足攻击角约束，给出了导弹三维制导控制一体化设计方法，使用微分几何方法对导弹三维制导控制一体化模型进行了反馈线性化，进一步基于特征结构配置方法根据期望性能来设计系统结构，仿真结果验证了该方法的有效性。如何在本文研究结论的基础上考虑执行机构的特性对制导控制一体化设计的影响，从而进一步提高导弹制导控制系统的动态性能，是需要深入研究的内容。

［1］ MENON P K，OHLMEYER E J.Nonlinear Integrated Guidance-Control Laws for Homing Missiles［R］.AIAA －2001 －4160，Montreal，Canada，Optimal Synthesis Inc，2001.

［2］ SHARMA M，RICHARDS N.Adaptive，Integrated Guidance and Control for Missile Interceptors［R］.AIAA －2004－4880，Providence，Rhode Island，Barron Associates，Inc，2004.

［3］ IDAN M，SHIMA T，Golan O M.Integrated Sliding Mode Autopilot-Guidance for Dual Control Missiles［R］.AIAA －2005－6455，San Francisco，California，Israel Institute of Technology，2005.

［4］ XIN M，BALAKRISHNAN S N，OHLMEYER E J.Integrated guidance and control of missiles with θ-Dmethod ［J］.IEEE Transactions on Control Systems Technology，2006，14（6）:981－992.

［5］SONG J M，ZHANG T Q.Passive homing missile’s variable structure proportional navigation with terminal angular constraint［J］.Chinese Journal of Aeronautics，2001，14（2）:83 －87.

［6］ HOU Mingzhe，DUAN Guangren.Integrated guidance and control of homing missiles against ground fixed targets［J］.Chinese Journal of Aeronautics，2008，21:162－168.

［7］ WILLIAMS D E，RICHMAN J，FRIEDLAND B.Design of an Integrated Strapdown Guidance and Control System for a Tactical Missile［R］.AIAA －1983 －2169，New Jersey，Singer Company，1983.

［8］ 雷延花，陈士橹.基于微分几何方法的大迎角导弹解耦控制［J］.飞行力学，2003，21（4）:39－41.

LEI Yanhua，CHEN Shilu.Decoupled control for a high angle of attack missile based on differential geometry method［J］.Flight Dynamics，2003，21（4）:39－41.

［9］ 段富海，韩崇昭.动态逆方法和微分几何反馈线性化方法的对比［J］.自动化仪器仪表，2002，3:4－6.

［10］ 吴文海，沈春林，刘国刚，等.飞行控制系统设计的特征结构配置法［J］.哈尔滨工业大学学报，2002，34（5）:639－642.

WU Wenhai，SHEN Chunlin，LIU Guogang，et al.Application of eigenstructure assignment to design of flight control system［J］.Journal of Harbin Institute of Technology，2002，34（5）:639－642.

［11］ 李帆，周凤歧，周军.导弹基于特征结构配置的输出反馈解耦控制［J］.弹箭与制导学报，2001，21（3）:5－8.

LI Fan，ZHOU Fengqi，ZHOU Jun.Decoupling control for missile by output feedback eigenstructure assignment［J］.Journal of Projectiles;Rockets;Missiles and Guidance，2001，21（3）:5－8.

（编辑:刘素菊）