一种基于J-无损分解的性能加权函数优化设计

韩蕾， 傅绍文

（1.中国民航大学航空自动化学院，天津 300300;2.哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨 150080）

0 引言

H∞控制理论在线性时不变系统鲁棒控制方面一直担负着重要角色，而加权函数选择是其在实际应用中成功与否的关键。文献［1］通过L综合方法指出了伺服系统权函数选取的方向。文献［2］讨论了加权函数构造的一般化方法。伺服系统控制器设计的一个重要目标是达到系统的性能极限，性能加权函数优化反映了这种要求。一般而言，达到系统的最好性能，需要将闭环系统控制器与性能加权函数同时加以优化［3］。文献［4］给出频域内有限个频率点的性能加权函数优化算法，随着频率点选取数量增多，计算量非常大。文献［5］在系统状态空间内通过分解技术得出一种性能加权函数优化算法，但算法中矩阵乘积的可交换条件很难满足。

本文提出一种新的、易于计算的性能加权函数优化方法。首先利用闭环系统性能最优的条件，给出性能加权函数优化算法的迭代步骤。然后根据Bode积分关系以及H∞最优控制结果的全通特性，证明了算法的收敛性。最后基于J-无损分解方法给出了算法迭代过程中性能加权函数的更新公式。

1 性能加权函数优化方法

H∞控制经常将设计问题归纳成混合灵敏度问题，如图1所示。

图1 混合灵敏度问题Fig．1 Mixed sensitivity problem

其中:G（s）为被控对象;K（s）为闭环系统控制器;We（s）是性能加权函数，在控制器设计中可以调整;WT（s）是系统不确定性加权函数，在控制器设计中是固定不变的。混合灵敏度问题中用灵敏度函数S和补灵敏度函数T分别表示对系统的要求或约束，具体来说就是求解如下H∞优化问题，为

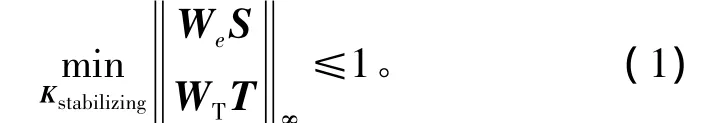
式中:S=（1+GK）－1;T=GK（1+GK）－1。所谓最优性能加权函数是指符合闭环系统性能要求且满足如下条件的Wep［6］，即

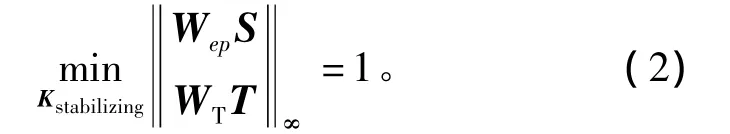
1．1 性能加权函数优化算法迭代步骤

We表征了闭环系统对干扰的抑制水平以及灵敏度要求，一般具有低通特性。给定初始的性能加权函数We0，求解H∞最优控制问题

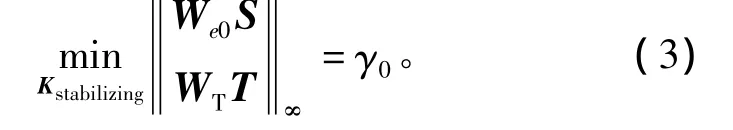
假定γ0<1。性能加权函数优化算法的指标可描述为:计算 Wep，满足式（2），且有 ¯σ（Wep（jω））>¯σ（We0（jω）），∀ω。

给出性能加权函数优化算法的迭代步骤为:

步骤一:给定初始性能加权函数We0，求解H∞

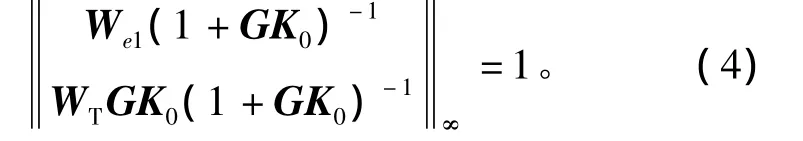
步骤三:令We0=We1，重复步骤一、二，直到闭环系统范数收敛到1。

1．2 算法收敛性分析

最优控制问题，得到最优控制器K0，闭环系统H∞范数 γ0。

步骤二:控制器固定为K0，求解We1，满足

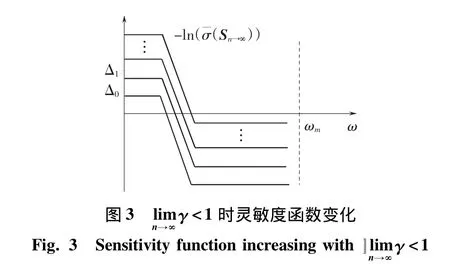
系统不确定性一般在高频影响显著，在系统不确定性影响较大的频段ω>ωm内，为保证系统鲁棒稳定性有‖GK‖∞≪1，ln（¯σ（S））≈0。由于 H∞最优控制设计结果使得闭环系统具有全通特性，即曲线 －ln（¯σ（S））与 ln（¯σ（We））之差 Δ（ω）在低频段0<ω<ωm上为常值，如图2所示。因此有

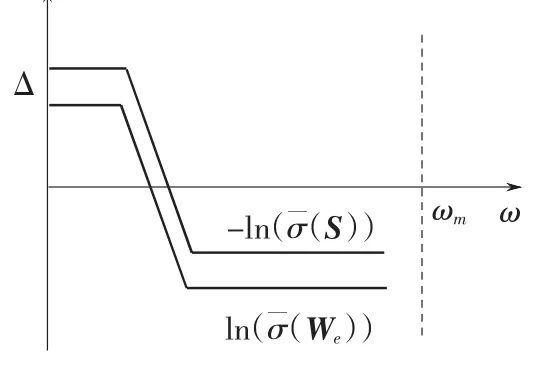
图2 性能权函数与灵敏度函数关系Fig．2 The relation between performance weight function and sensitivity function

1．3 基于J-无损分解的We1求取

下面讨论性能加权函数优化迭代算法步骤二中We1的求取，结果表明不必借助步骤一中的控制器K0，即可由 We0、γ0以及 WT得出 We1。

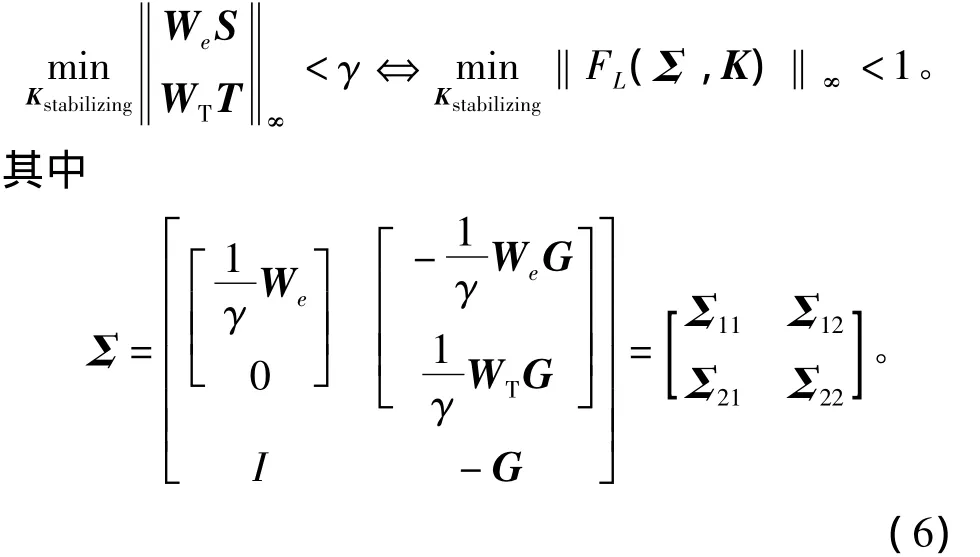
由于性能加权函数主要表征了系统对低频区域的要求，而系统的不确定性一般在高频较大，式（8）可简化为

此时，采用如上性能加权函数优化算法，满足前述指标要求:由算法收敛性证明过程可知随着迭代次数增加，闭环系统范数收敛到1，且有¯σ（We1（jω））>¯σ（We0（jω）），∀ω。其迭代步骤可简化为

步骤一:给定性能加权函数We0，求解H∞最优控制问题，得到闭环系统H∞范数γ0;

步骤二:令 We0=We0/γ0，重复步骤一，直到闭环系统范数收敛到1附近。

2 仿真实例

在图1所示的系统中，给定不确定性加权函数、被控对象传递函数以及初始性能加权函数为

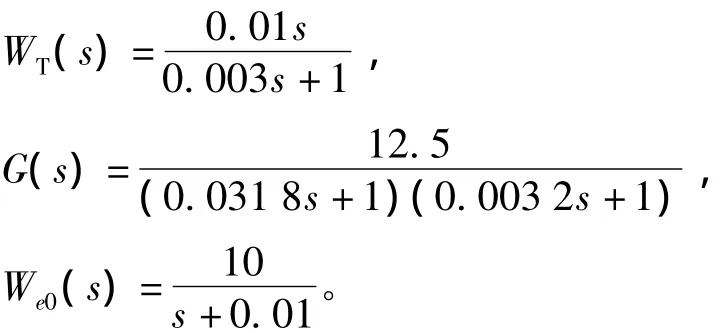
算法经过10次迭代后，闭环系统H∞范数收敛到0.992，得到最优性能加权函数为

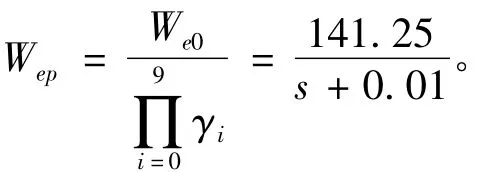
图4 算法迭代中闭环系统范数γFig．4 γ of the closed loop during algorithm’s iteration

3 结语

所提出性能加权函数优化算法具有非常简单的表达形式，易于迭代计算，且具有较快的收敛速度。虽然算法的得出是以混合灵敏度问题为背景的，但经过类似的推导过程可知对于一般的H∞控制问题该算法仍然适用。

［1］ 王广雄，何雨奋.伺服设计的性能极限［J］.电机与控制学报，1997，1（4）:238－240.

WANG Guangxiong，HE Yufen.Performance limit of servo design［J］.Electric Machines and Control，1997，1（4）:238 －240.

［2］ 王曦，曾庆福.频域不确定性系统加权混合灵敏度函数频域整形［J］.航空学报，1999，20（4）:358－361.

WANG Xi，ZENG Qingfu.Frequency shaping of mixed weighted sensitivity function for frequency uncertainty systems［J］.Acta Aeronautica et Astronautica Sinica，1999，20（4）:358－361.

［3］LANZON Alexander.Weight Optimisation in H∞Loop-shaping［J］.Automatica，2005，41:1201 －1208.

［4］LANZON Alexander.Pointwise in frequency performance weight optimization in μ synthesis［J］.International Journal of Robust and Nonlinear Control，2005，15（2）:171 －199.

［5］LANZON Alexander.On the formulation and solution of robust performance problems［J］.Automatica，2003，39（11）:1707－1720.

［6］ 王广雄.H∞控制中的LMI法.电机与控制学报［J］.1997，1（2）:71－74.

WANG Guangxiong.On the LMI Approach to H∞Control［J］.E-lectric Machines and Control，1997，1（2）:71 －74.

［7］ GREEN M，GLOVER K，LIMEBEER D，et al.A J-spectral factorization approach to H∞control［J］.SIAM Journal of Control and Optimization，1990，28（6）:1350－1371.

（编辑:刘素菊）