两种衰变分支比的研究
黄亚伟
(文山学院数理系,云南文山 663000)
第一种衰变分支:当核素发生的是同时具有几种不同形式的放射性衰变时,则每一种形式的衰变构成了一个衰变分支。如同时有β-、β+和 EC中的两种或三种,就将有相应的两或三个衰变分支。
第二种衰变分支:核素发生的是只有一种形式的放射性衰变(如只有β-衰变),但母核可能衰变到子核的不同能态(即不同的特定能级),这时,对应子核的不同的特定能级,β-衰变的Emi、比较半衰期将各不相同。这样就构成了另一种分支衰变中不同的衰变分支。
对第一种衰变分支概念的应用,符合通常采用的方法。即半衰期T1/2=(ln2)/λ是反映放射性核衰变过程的一个重要物理量,它与反映原子核衰变概率的衰变常量λ成反比。当核素具有多种分支衰变时,按衰变常量的物理意义,总的λ应当是各种衰变方式的部分衰变常量λi之和:λ=∑λi。第i种分支衰变的部分放射性活度为Ai=λiN0e-λt,总的放射性活度为A=∑Ai=λN0e-λt,由此定义衰变的分支比

在很多时候对半衰期概念的应用是与部分衰变常量相对应的部分半衰期,定义为
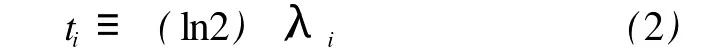
但它只能通过(1)式计算得到,而不能通过测量部分放射性活度的衰减直接得出。由(2)式可见ti与λi成反比,即
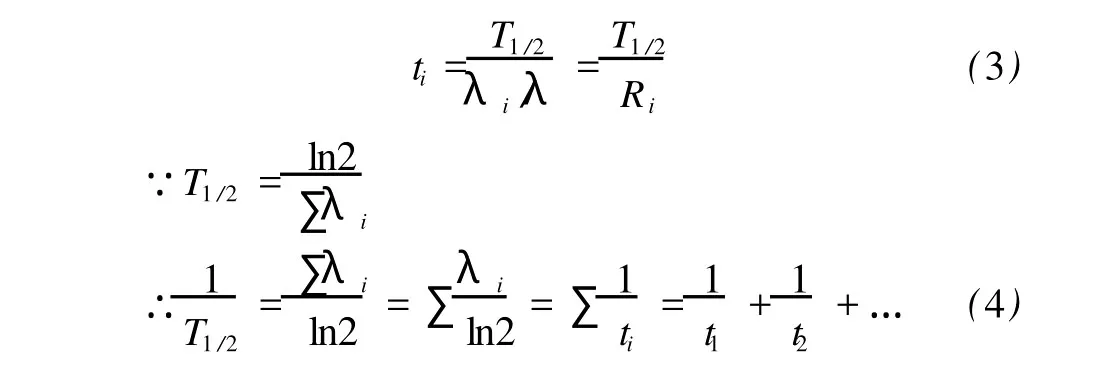
(3)式给出部分半衰期与衰变的分支比的关系,而(4)式则指出了整个系统衰变的半衰期与各分支部分半衰期的关系。可见,T1/2比任何一个ti都小,这说明总的核素衰变比每一种分支衰变都要快。
对第二种衰变分支概念的应用则不同,下面进行分析。
1 比较半衰期及其引伸
1.1 比较半衰期的概念和问题的提出
β衰变的费米理论导出了β衰变的基本公式,并由此给出T1/2和λ与β粒子的最大能量Em的关系(萨金特定律):T1/2∝1/Em5或λ∝Em5。可见,半衰期和跃迁概率与β粒子的最大能量有强烈的依赖关系。由于能量的不同,即使对于同一类型的跃迁,半衰期可以相差很大,例如超容许跃迁,有的甚至达到 109。所以仅仅半衰期不能反映跃迁类型的特征。
为了反映不同跃迁类型的特征,一般引入比较半衰期[1-3]
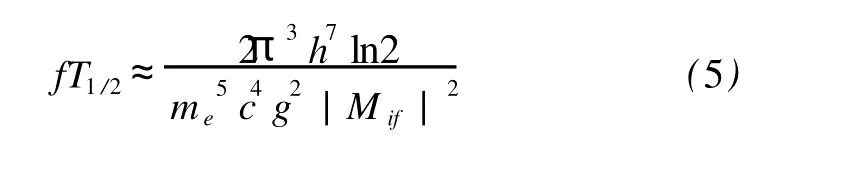
可见,比较半衰期fT1/2值与跃迁矩阵元的平方|Mif|2成反比。由于Mif对不同级次的禁戒跃迁有很大差别,故对任一β衰变,fT1/2是直接反映跃迁矩阵元大小的最重要的量,从而fT1/2可以比较跃迁的级次。fT1/2值都是很大的数,而且变化范围很广,所以通常用 logfT1/2值来表示。其中,fT1/2是取秒作单位时的数值。常见各级跃迁 logfT1/2的值的大致范围见文献[1]。fT1/2另一重要用途是,用它可以确定β衰变的弱相互作用常数g值。有的文献[3]将比较半衰期 logfT1/2作为β跃迁级次的选择定则之一,通常用 logfT1/2来判断跃迁级次是相当准确的。
实验所能观测到的只是总的半衰期,即(4)式的T1/2。所以一般文献[1-3]中定义的比较半衰期fT1/2或 logfT1/2,是针对母核发生单一形式的β衰变,到子核某一能级而言的。但是,常常会发生一个原子核同时进行几种不同形式的放射性衰变的情况,这就是分支衰变。当把它应用于衰变具有多个分支,到子核某个特定能级的衰变过程时,将发现是非常粗糙和笼统的。就是说,要描述分支衰变或者说对于每一分支比,它变得无能为力,需要寻找更细致的描述方式。
1.2 跃迁到某一特定能级的部分比较半衰期
在多数的β谱中往往存在着多群(两群或两群以上)的β射线,不同β射线对应不同的β衰变。每一β衰变有其β粒子最大能量Em,i、子核能级Ei和相应的比较半衰期,但该比较半衰期如上所述,与和T1/2对应的比较半衰期是不一样的。为把二者区别开来,这里提出跃迁到某一能级的比较半衰期或者称为部分比较半衰期的概念,定义为fti。同样因其数值较大仍可用其对数值 logfti表示。这样对该分支衰变到子核某个特定能级而言,就可以通过fti或 logfti准确地描述其衰变时间及寿命。要注意的是其对数形式只能用来表示每一分支发生衰变的比较半衰期,而不能用来计算总的比较半衰期,否则将会很复杂或出现错误的结果。
由(4)式,原子核衰变的比较半衰期与部分比较半衰期的关系为

即要通过各部分比较半衰期(不能取对数)倒数求和,再取其倒数的对数,才能得到原子核总的比较半衰期 logfT1/2。
根据各群β射线费米标绘的数据,可以把一群β射线的β谱曲线画出来,计算其曲线下的面积即得每群β射线的强度,由此可以得到各群β射线的相对强度Ii(通常用百分比表示)。再根据从实验所得到的半衰期T1/2和式
I1t1=I2t2=…=Intn(7)可以得到每一β射线的fti或 logfti值。
测定和分析各个β射线的相对强度Ii值和γ射线所得到的数据相配合,可以用来确定原子核能级特性,以作为研究原子核结构的依据。
2 从核衰变实验结果提取分支比和部分比较半衰期
2.1 101M o的β-衰变实验结果
文献[4]给出了101M o的β-衰变和101Tc能级跃迁实验结果图。101M o核发生β-衰变后成为101Tc核,通过γ衰变由较高激发态向低态跃迁,最后回到基态。图中显示,成为β-衰变子核101Tc的状态能级有 44个。在由101M o衰变到101Tc的不同能级,以及由101Tc的高态能级跃迁到不同的低态能级时,形成了许多不同的衰变分支。沿着每一分支的衰变在整个衰变系统中占有一定的概率,用分支比Iε表示。分支比Iε越大,意味着衰变的强度也越大,也就是衰变的概率越高。图中的Iε即衰变的分支比:Iε=λi/λ,显然 ∑Iε=100%。每一个Iε除由实验直接测量外,还可以从101Tc的γ衰变中从能级跃迁的强度平衡中间接简单计算得到:Iε等于由该能级向下跃迁的分支比(强度)之和∑I′ε与跃迁到该能级的分支比∑I″ε之和二者的差值,即
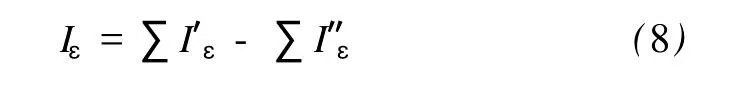
2.2 从实验结果计算衰变分支比
以101M o基态跃迁到101Tc的 1 319.57keV激发态为例,见表 1。该β-跃迁的几率是Iε=6.63%;跃迁到该能级的比较半衰期是 logfti=6.119,属一级禁戒跃迁(非唯一型);理论自旋值范围是 3/2和5/2,宇称为正。
对能级 1 319.57keV计算Iε值。这里Iε的值就是(3)式中的衰变分支比Ri,即Iε=Ri=λi/λ,可由101Tc核γ射线测量实验中得到,见表 1。该能级向低态跃迁时发出四条谱线(射线能量),测出相应的谱线强度I′ε,它们的总强度是∑I′ε=8.02;到该能级的跃迁也是四条谱线,相应的谱线的强度为I″ε,其总强度 ∑I″ε=1.387。二者之差为 ∑I′ε-∑I″ε=6.63,正是衰变到101Tc的 1 319.57keV激发态的强度或分支比Iε。可见,关于β-衰变到每一能级的强度(跃迁的正常化强度或强度标准)或分支比可以从该能级的γ跃迁强度平衡中得到。应用Iβ-理论值可以对有关β-的每一个能级的强度作出计算,β-衰变到基态的相对强度由跃迁到的能级减少的相对β-强度计算出来。然后,从每一个能级可获得重正化系数和β-的衰变分支比[4]。

表1 101M o基态经β-衰变到101Tc能级 1 319.57keV的分支比
2.3 从实验结果提取比较半衰期
文献[4]的实验结果图给出了101M o基态经β-衰变到101Tc基态的半衰期T1/2=14.61m in,以及衰变到101Tc各能级的比较半衰期的对数值 logfti,由图中可以看出101Tc的 logfti值在 4.330~9.538之间,即101M o的部分比较半衰期 logfti最大值与最小值之间相差 5个量级。
logfti的计算:f可以通过数值积分或查阅曲线表得到。这里,如用数值积分计算f,则它依赖于β-粒子的最大能量Em。对101M o基态经衰变到101Tc基态,Em=Q+=2 824±24keV;对衰变到101Tc的其它能级Ei,Emi=Q+-Ei。而ti,由(3)式
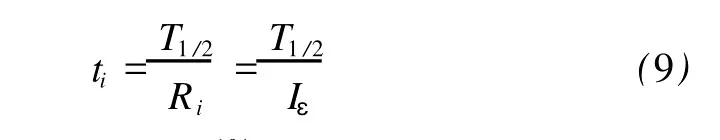
对101M o的β-衰变子核的101Tc每一能级,由(7)式求出相应的Iε,在已知T1/2时,由(9)式即可求得ti。于是得到部分比较半衰期fti,进而表示为logfti。
3 结 语
综上所述,跃迁到某一能级的比较半衰期或者称为部分比较半衰期ft1/2,i或 logft1/2,i,与针对整个核衰变系统而言的比较半衰期fT1/2或 logfT1/2是两个层次的概念,具有不同的对象。前者和部分衰变常量λi及衰变分支比Iε(或Ri)相联系,后者则和整个原子核衰变的衰变常量λ相联系,在研究和表述中应注意区别开来。
[1] 卢希庭.原子核物理 (第二版)[M].北京:原子能出版社,2000:151-154.
[2] 梅镇岳.原子核物理学,(第二版)[M].北京:科学出版社,1966:226-231.
[3] 王永芬.原子核物理学基础 (上册)[M].北京:清华大学出版社,1986:226,250.
[4] SHENG Shuifa,WANG Fengge,GU Jiahui,et al.Decay of 101Mo and Band Structures of its Daughter Nuclide 101Tc in the Projected Shell Model[J].Journal of the Physical Society of Japan,2006,(1):014201.

