一道例题的有效变式练习——一元二次函数图像与x轴交点例题的教学案例

✿浙江省海盐县教研室 沈顺良

一道例题的有效变式练习
——一元二次函数图像与x轴交点例题的教学案例

✿浙江省海盐县教研室 沈顺良

例题是具有一定代表性的典型问题，变式练习能有效地引导学生探究并理解知识实质，也能将所学知识进行拓展，下面试呈现一个例题的有效变式练习.

1.铺垫式练习：

求y=x2-3x+2的图像与y轴的交点坐标.

师：函数图像与y轴的交点是一个几何特征，能否直接由图得到？

生：不能准确地得到.

师：那可否由函数解析式用代数方法得到？

生：可以，y轴上的点满足条件x=0，因此将x=0代入可得y=2，从而函数图像与y轴交点坐标为（0，2）.

师：从本题可以看出，当函数图像的几何特征用几何方法难以求出时可以用函数表达式借助代数方法来解决，函数图像本身是满足函数关系式的（x，y）所对应点的集合，这时必须清晰它们之间的转化.

【点评：（1）通过铺垫问题解决探究的过程引导，渗透了函数问题解决中的数形结合思想，这在二次函数教学中也是一个重要任务；（2）辅助理解，分散难点.相对函数图像与x轴的交点来说，函数图像与y轴的交点较易理解，有了这样的铺垫，借助正迁移能帮助学生解决理解函数图像与x轴交点这一难点.】

2.例题练习：

求y=x2-3x+2的图像与x轴的交点坐标.

师：上题中函数图像与x轴交点转化为函数y=x2-3x+2中当x取0时对应的y值，那么类比上题，函数图像与x轴交点是什么？

生：同样由图像难以得到，由于x轴上的点满足y=0，故对应于函数y=x2-3x+2中当y取0时的点.

师：那如何求？

生：和上面类似，将y=0代入得x2-3x+2=0，（x-1）（x-2）=0，解得x1=1，x2=2，从而得到所求交点为（1，0），（2，0）.

师：本题的解决包含了哪些转化问题？

生：与上题一样有几何到代数的转化，还有是函数到方程的转化.

【点评：有前面问题解决做铺垫，学生容易理解函数图像与x轴交点即为纵坐标（函数值）取0时所对应的点，又有上题的转化铺垫，学生也自然想到将问题转化为代数解方程来解决，后面的引导性问题渗透了数学思想的运用.】

3.理解性变式练习：

求y=x2-3x+2的图像与直线y=2的交点坐标.

师：此问题与上题有何关系？

生：就是将上题的y=0改为y=2，因此转化也是类似的，即是函数y=x2-3x+2图像中函数值（纵坐标）取2时对应的点.

师：具体如何求呢？

生：将y=2代入转化为方程x2-3x+2=2，即x2-3x=0，方程的解为x=0，x=3，因此函数图像与x轴的交点为（0，0），（3，0）.

【点评：通过将函数图像与x轴的交点变式为与直线y=2的交点，更从一般意义上让学生理解到函数图像上的具体点即是纵（横）坐标已知下求横（纵）坐标，从而将几何问题转化为代数问题，将函数转化为方程来解决.】

4.探究式变式练习：

求y=x2-3x+3的图像与x轴的公共点个数.

师：如何求与x轴公共点个数呢？

生1：与x轴公共点即满足y=0，也就转化为先求方程x2-3x+3=0的解.

生2：方程是无解的，因为b2-4ac=-3＜0.

师：对，那公共点个数怎么样？

生2：应该是没有公共点的.

师：不错，从这里我们知道了利用方程的工具来解决函数问题.那么你能否得到y=ax2+bx+c（a≠0）的图像与x轴的公共点个数？

生3：同样可转化为方程ax2+bx+c=0的根的个数，得到b2-4ac＞0时有两个公共点，b2-4ac=0时有一个公共点，b2-4ac＜0时有没有公共点.

【点评：通过变式问题的探究过程，更突出了函数图像与x轴公共点即为函数值为0时对应方程的根的问题，并且能全面地认识函数图像与x轴公共点的情况.】

5.拓展化变式练习：

（1）下列命题：若b2-4ac＞0，则二次函数y=ax2+bx+c的图像与坐标轴的公共点的个数是2或3，该命题正确吗？

【分析：题中条件可以推出方程有两个不等实数根，对应到函数的图像则与x轴有两个公共点，再加上它与y轴的公共点得到结论成立.】

（2）y=ax2+bx+c（a≠0）的图像与坐标轴的公共点个数？

【分析：在分类讨论中把握二次函数图像与坐标轴的公共点问题.】

（3）利用图像解一元二次方程x2+x-3=0时，我们采用的一种方法是：在平面直角坐标系中画出抛物线y=x2和直线y=-x+3，两图像交点的横坐标就是该方程的解.利用图像解一元二次方程x2+x-3=0，也可以这样求解：在平面直角坐标系中画出抛物线y= 和直线y=-x，其交点的横坐标就是该方程的解.

【分析：两个函数图像的交点即为两个函数图像上纵坐标相等时所对应的同一横坐标，此即为代数形式中的方程.方程x2+x-3=0的解可以将其转化为函数y=-x和y=-x2-3的图像交点的横坐标.】

（4）已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图像相交于点A（-2，4），B（8，2）（如下图所示），则能使y1＞y2成立的x的取值范围是 .

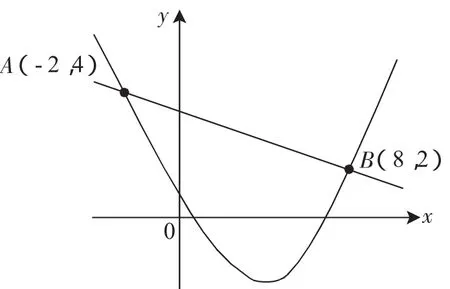
【分析：即使将A、B两点坐标代入也不能求出其中二次函数解析式，但观察图像可直接得到不等式的解为x＜-2或x＞8.】

【点评：通过近年来中考试题等新颖试题的要求，其中有一次函数、二次函数等，有求交点个数，有求方程的解，还有不等式的求解，它们从本质上要求学生理解函数问题解决中的数形结合运用，理解函数方程工具的运用.】

E-mail:hit790205@163.com

❖编辑/张烨