对一道传统习题答案的商榷

柯尊淦 陈巨华

(佛山市第一中学,广东佛山 528000)

对一道传统习题答案的商榷

柯尊淦 陈巨华

(佛山市第一中学,广东佛山 528000)

图1

题目:如图1所示,质量为2m和m.可看作质点的小球,用不计质量的不可伸长的细线相连,跨在固定的半径为R的光滑圆柱两侧,开始时A球和B球与圆柱轴心等高,然后释放两球,则球到达圆柱体最高点时的速率是多少?

笔者在讲解机械能守恒定律这节课时,翻阅了很多教辅资料,例如:未来出版社《世纪金榜》(物理必修2)第52页典型题3;光明日报出版社《名师一号》(粤教版物理必修2)第83页巩固练习1;广东省出版集团《名师大讲堂》(物理必修2)第63页例4;中国少年儿童出版社《教材解析》第186页例题6,《高中物理解题方法》(物理必修2)第187页第16题等等,都能看到上面这道题目.这些参考书给出的标准答案如下:

解析:选轴心所在水平面为参考平面,刚开始时系统的机械能E1=0;当A、B两球运动到如图2状态时,系统的机械能为

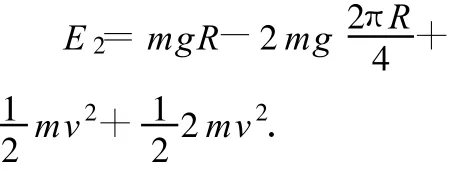
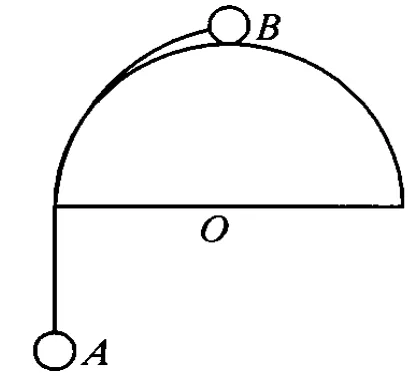
图2

根据系统机械能守恒定律有E1=E2,解得

分析:以上解法看上去天衣无缝,其所给的结果一定是正确的吗?不妨对B球做以下的分析(如图3):对B球在最高点有

图3

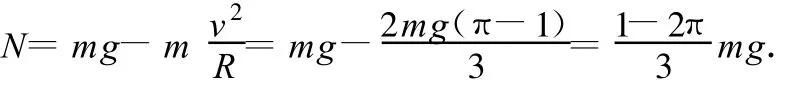
拓展1:那么本题中B物体在圆柱体哪个位置会脱离圆柱面呢?

解析:不妨假设B球上升到θ的位置时(如图4),对AB系统由机械能守恒可得

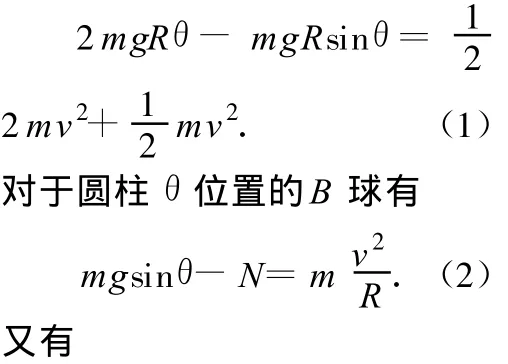
图4

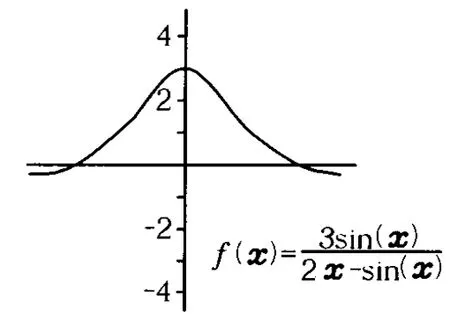
图5

该函数是一超越函数,不能得到代数解,只能采用数值解法.采用几何画板工具可得到如图5的图像.函数图像与横坐标的交点即为该函数的解为θ≈1.13rad,故B球在距离圆柱底面角度为1.13弧度的位置就脱离了圆柱面.

拓展2:那么要使得B球能够达到最高点,则对A、B两球的质量有什么要求?

解析:不妨假设B球上升到θ的位置时,对AB系统由机械能守恒可得

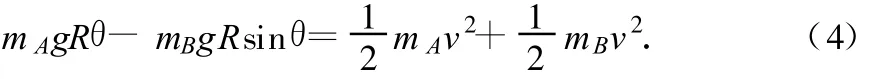
对处于圆柱θ的位置B球可得

讨论:

本题本是一道考察系统机械能守恒定律的好题,但是出于科学性和严谨性的考虑,笔者对标准答案提出以上质疑和讨论.为了避免问题的出现,建议把问题设置为:要使得B球能达到圆柱最高点,对A、B的质量有什么要求?

2010-06-03)

#物理·技术·社会#