基于H∞理论的交会对接模拟器横向平移控制系统设计*

李贵明，姚 郁

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190；3.哈尔滨工业大学控制与仿真中心，哈尔滨150001）

基于H∞理论的交会对接模拟器横向平移控制系统设计*

李贵明1，2，姚 郁3

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190；3.哈尔滨工业大学控制与仿真中心，哈尔滨150001）

研究九自由度空间交会对接模拟器横向平移控制系统设计问题.采用非结构不确定性描述系统中的高频机械谐振，给出了系统对象的不确定性模型.根据横向平移系统的性能指标和主要不确定性确定了鲁棒H∞控制方案，并研究了混合灵敏度问题的加权函数选取原则和确定方法，给出了基于线性矩阵不等式（LMI）的H∞控制律的存在条件和设计方法.实际系统测试结果达到指标要求，说明了该方法的有效性.

空间交会对接模拟器；横向平移控制；H∞控制

空间交会对接是载人航天工程的重大课题［1］.导航、制导与控制系统使两飞行器在对接前的相对位置、姿态和速度都满足一定要求，对接机构接触碰撞并自动相互锁紧，最后完成对接任务.

九自由度空间交会对接模拟器用于模拟交会过程中最后段内的相对运动，对接任务决定模拟器应具备九个自由度.模拟器采用6＋3的系统方案，其中的追踪飞行器的六自由度由三个姿态运动和三个平移运动组成.要求模拟质心运动的三个平移运动具有大行程和严格的垂直度，还要求平移系统满足低速平稳性和稳态精度等指标.

自从1981年Zames提出将H∞范数作为系统设计的工具、开创H∞控制理论以来，经过二十多年的发展，H∞控制理论已进入完善和推广时期，是解决不确定系统控制问题的一种综合方法［2］.针对机电伺服系统，可根据系统的鲁棒稳定性和鲁棒性能要求直接设计出H∞控制器，是一种系统化的设计方法.H∞控制问题的基于LMI（linearmatrix inequality）的求解方法，需要的假设条件相对较少［3］，把问题转化为求解三个线性矩阵不等式的凸优化问题，采用“内点法”进行求解.

本文以空间交会对接模拟器横向平移控制系统设计为背景，采用了鲁棒H∞控制方案，研究了加权函数的选取原则，给出了基于LMI的H∞控制律存在条件和求解方法，并给出了实际系统的测试结果.

1 横向平移系统结构和不确定性描述

模拟器横向平移系统结构如图1所示.选定哈尔滨工业大学自主研制的交流无刷力矩电机，该电机设计成中空结构，丝杠从电机轴心穿过，电机转子直接带动螺母旋转，采用旋转螺母滚珠丝杠传动为本系统的传动方案.

图1 横向平移系统结构

平移系统的被控对象由交流电机本体、逆变驱动电路和位置传感器组成，通过机理分析推导出其传递函数为

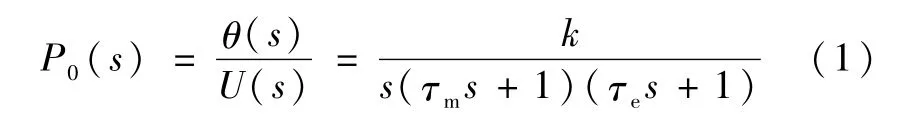
式中，U（s）为电机驱动器的输入电压，θ（s）为旋转变压器的输出位置，τm、τe分别为机电、电气时间常数.

横向平移系统的模型可通过输入变频正弦信号辨识得到.由于受系统自身条件限制，测试不能达到很高的频段，导致了高频未建模的动态.而作为机械系统固有特性的机械谐振在高频区表现尤为突出［4］.根据工程实践经验，可将其表述为如下形式：

式中，ω0为谐振峰频率，a／b为谐振峰值.谐振特性由机械结构决定，且难以准确描述，只可根据实际测试数据确定出机械谐振引入的不确定性的界.考虑到未建模特性是非结构不确定性，故采用乘性摄动加以描述，即实际对象P（s）为

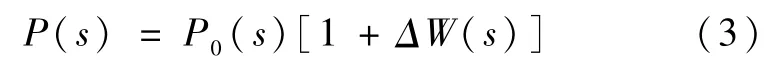
式中‖Δ‖∞≤1，界函数W（s）有待于设计.乘性不确定性可由图2来描述.

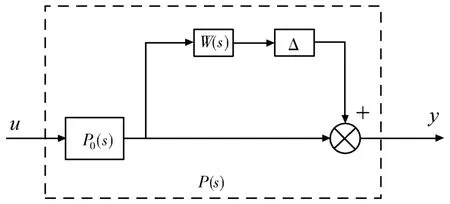
图2 对象乘性不确定性描述框图

2 基于LM I的H∞控制律

2.1 混合灵敏度问题与标准H∞控制问题

考虑了不确定性、鲁棒稳定性和鲁棒性能的伺服系统的H∞控制问题可以表述为如图3所示的混合灵敏度问题［5］.

图3 混合灵敏度设计的系统框图

图3中r、e、u、d和y分别为参考输入、跟踪误差、控制输入、干扰输入和系统输出.从r至e，u和y的闭环传递函数分别为

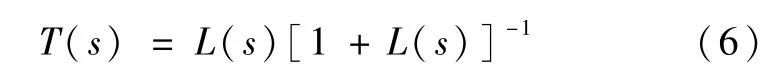
式中，L（s）＝P0（s）K（s）为系统开环传递函数.通常S（s）和T（s）分别称为灵敏度函数和补灵敏度函数.

控制器设计的目标为通过最小化r到z1的传递函数来满足跟踪和抑制干扰的性能；最小化r到z2的传递函数来防止系统饱和、调整系统带宽；最小化r到z3的传递函数来满足鲁棒稳定性，即

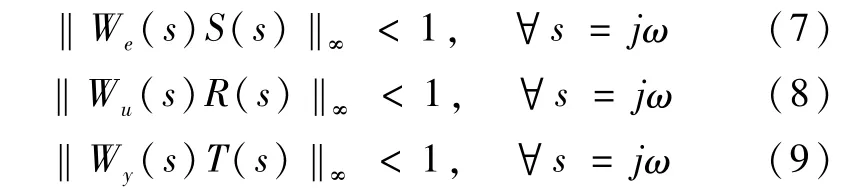
式（7）～式（9）是考虑不确定性上限情况下，系统满足鲁棒稳定性的条件.联合三式可知，设计任务就是寻找控制器K（s）使

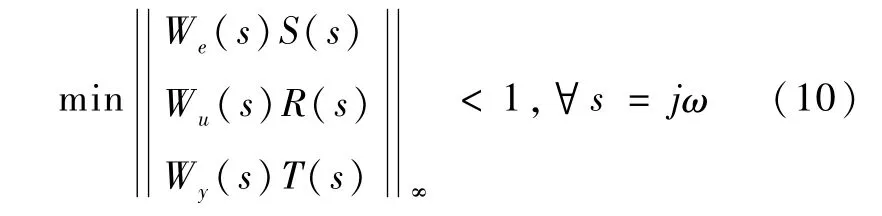
成立.

混合灵敏度问题便于通过系统频域指标进行设计，但没有统一的解法.将图3稍加变换可得如图4所示的标准H∞控制结构.因此，可以通过求解标准H∞控制问题来求解混合灵敏度问题［6］.

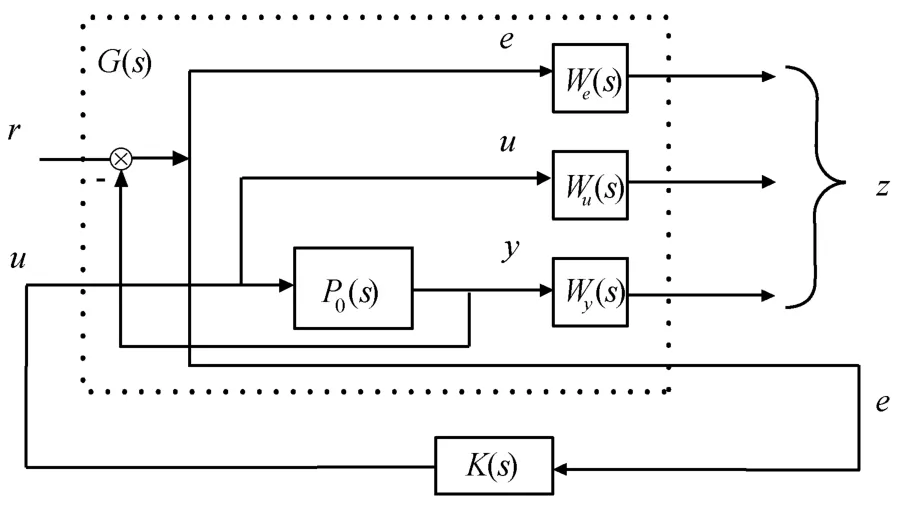
图4 标准H∞框图

2.2 加权函数的选取原则

下面分别给出各加权函数的选取原则［7］.

（1）跟踪性能加权函数We（s）的选取原则

We（s）代表干扰的频谱特性.在We（s）的选取中要考虑低频干扰的频带宽度、按系统快速性要求确定的剪切频率和噪声抑制比例.因此选取的形式一般为

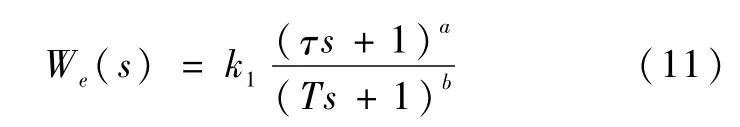
式中，k1为比例系数，T和τ为时间常数.首先通过综合性能指标确定其阶次，然后根据跟踪带宽确定参数T，根据噪声抑制性确定参数τ，最后根据We（s）对高低频增益的要求以及性能指标γ值确定参数k1.

We（s）一般采用低通的形式.低通部分是为了保证系统的低频高增益，以满足系统的跟踪性能；高频段降低增益是为了抑制高频干扰信号的影响.为了提高平移系统性能，取We（s）的由低频高增益到高频低增益的斜率为－40dB／dec，即

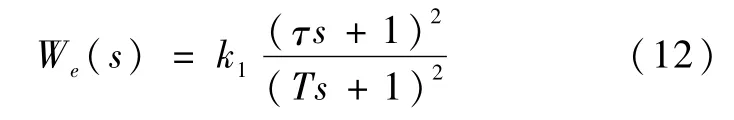
（2）输出加权函数Wy（s）的选取原则

因Wy（s）表示乘性摄动的范数界，代表模型中存在的高频未建模动态，因此应具有高通特性.其斜率可以取的大些，以保证闭环系统对高频干扰的抑制效果.

（3）控制量加权函数Wu（s）的选择原则

因Wu（s）表示加性摄动的范数界，代表模型中存在的中低频参数不确定性，因此应该具有低通特性，一般取为惯性环节或常数.当中低频参数摄动是非主要不确定性时，通过其得到合适的控制量即可.本系统中Wu（s）的作用是保证控制电压处于±10V之间，以便实现数字控制.

2.3 基于LM I的H∞控制律

为便于求解K（s），引入下面的引理.

引理1［8］.设E，F，Q为已知矩阵，且QT＝Q，则存在矩阵X，满足

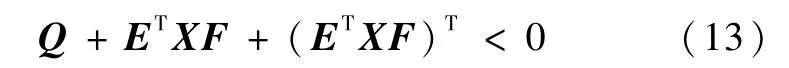
的充分必要条件是

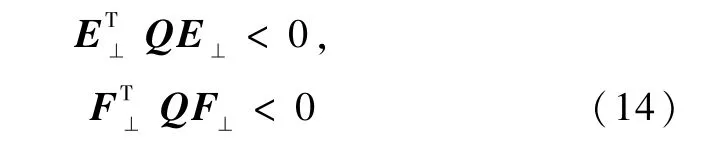
式中，矩阵E⊥，F⊥分别是E和E⊥的垂直补.

设P0（s）的状态空间实现为（AP0，BP0，CP0，DP0）；We的状态空间实现为（AWe，BWe，CWe，DWe）；Wu的状态空间实现为（AWu，BWu，CWu，DWu）；Wy（s）的模型为Wy（s）＝CWy（sI－AWy）－1BWy＋Tmsm＋…＋T1s＋T0.

（3）教师对作业的设置缺乏系统性。作业的设计必须根据课程标准、教材和学生的实际学习需要，系统地考虑年级、单元、课时的连贯性和一致性，符合语言学习的规律，兼顾听、说、读、看、写能力的全面发展。教师对作业的设计缺乏与生活实际的联系和趣味性，导致学生产生排斥心理，持敷衍应付的态度完成作业。

由图4可知，广义输入r、u，广义输出z、e和广义被控对象G之间满足

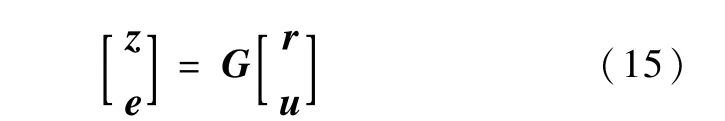
其中

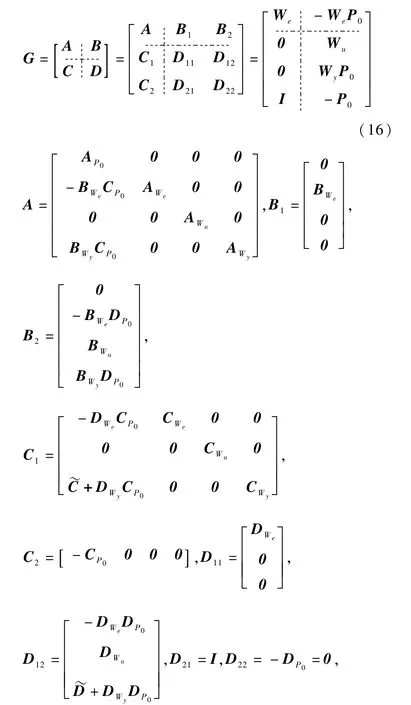
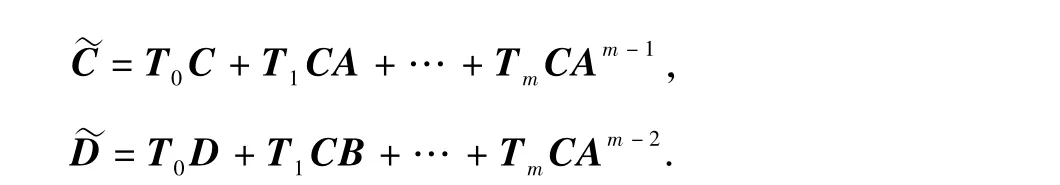
引理2［3］.设广义对象G满足（A，B2）可镇定、（A，C2）可检测，则存在使图4所示的系统内部稳定、且满足‖Hzw‖∞＜γ的控制器K（s）的充分必要条件为下述LMI：

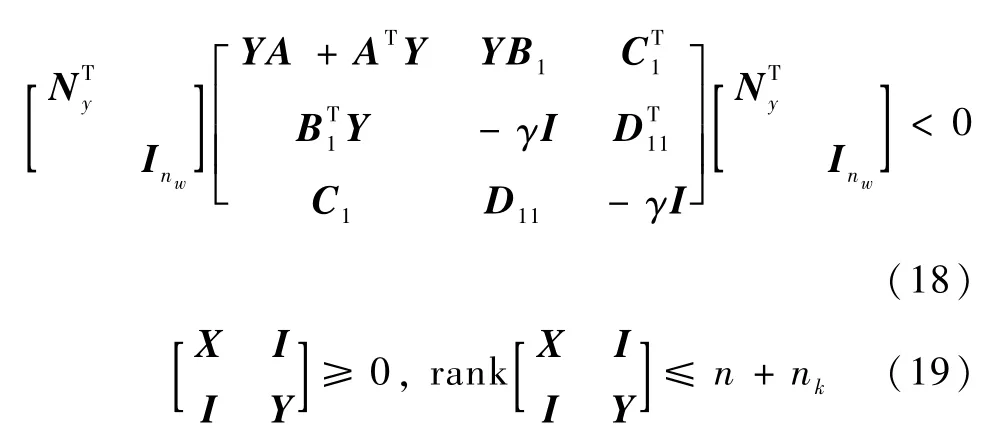
存在解矩阵X＞0和Y＞0.其中n和nk分别表示G和K的次数.

根据引理1和引理2及其证明过程，可得H∞控制律的存在条件和设计方法.

3 横向平移控制系统设计

3.1 被控对象测定

系统处于开环状态，给定正弦电压指令幅值为6 V，从0.1 Hz扫频至40 Hz得到被控对象的频率响应曲线族）.取的中心线为标称对象P0（s），通过调整式（1）中的三个参数，采用最小二乘法对P0（s）进行拟合，得P0（s）为

根据

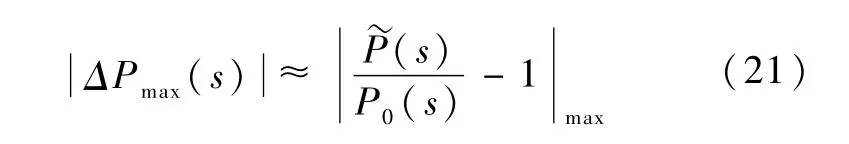
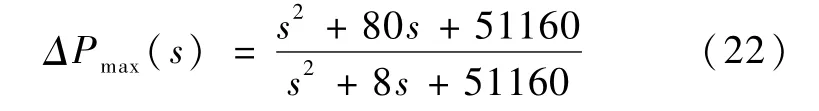
式（22）证实，高频不确定性为机械谐振.考虑到鲁棒控制器的阶次与其有关，并结合加权函数的意义和选取原则，取Wy（s）为

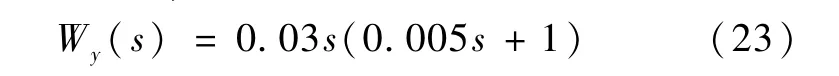
3.2 性能加权函数确定

横向平移系统的主要性能指标为：

1）闭环系统动态响应满足：幅度误差小于10%、相位滞后小于10°的带宽高于0.5 Hz；

2）位置伺服误差：±1mm；

3）最低平稳速度：1mm／s.

下面将结合性能指标进行基于γ值的We（s）的参数确定.

将乘性不确定性加权函数Wy（s）重新列写，如式（24）所示，并选取控制量加权函数Wu（s）如式（25）所示

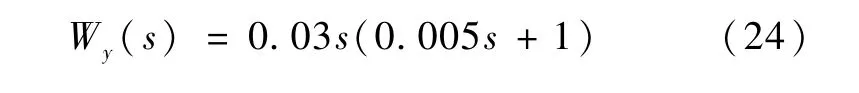
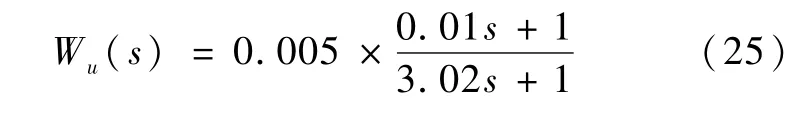
根据指标要求1），设定两个转折频率分别为1 Hz和10 Hz，即

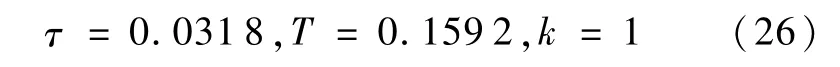
由于此时We（s）的频域特性转折段较窄，导致了低频高增益和高频低增益只相差25 dB.考虑到高频低增益是为了抑制高频干扰，取

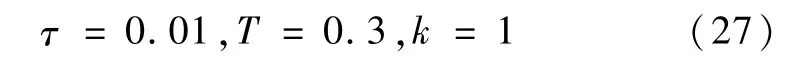
则We（s）的高低增益之间相差60 dB，并且0.5Hz处于惯性环节的转折频率前.由于r＝0.125 9，考虑到增大k可更有效抑制10Hz以上的高频扰动，故取k＝20时，γ＝0.706.继续增大k，使We（s）低频增益再高些，且将γ值逼到1附近.最后选定γ值小于1时的k的最大整数值33，相应的γ＝0.983.即最终确定的We（s）为

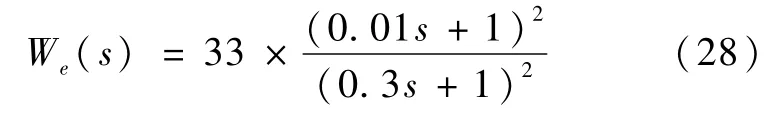
综上，混合灵敏度问题的三个加权函数的幅频特性如图5所示.

3.3 H∞控制律与系统鲁棒稳定性

利用式（16），可得变换后广义对象的系统矩阵G为

根据广义对象G，利用引理2

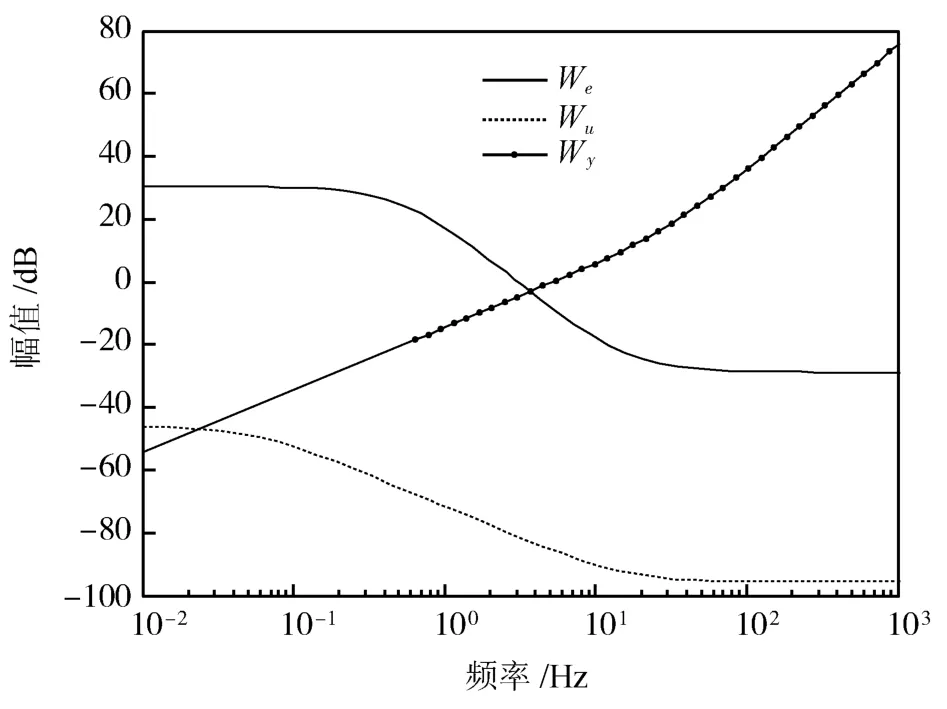
图5 加权函数的幅频特性

求得H∞控制律K（s）为

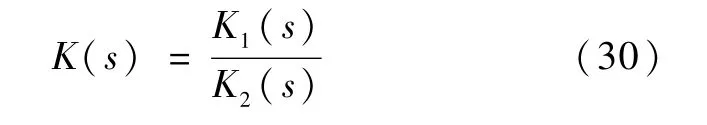
式中，

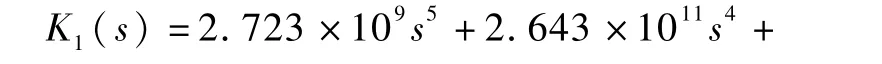
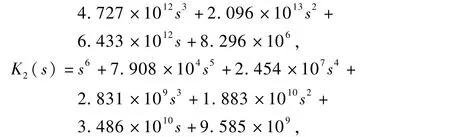
这是一个6阶的线性控制器，相应的H∞最优性能指标为γ＝0.983.

考虑到本系统采用W indows2000与RTX相结合的定时机制以保证计算机控制系统采用周期为0.5ms，因此在T＝0.5ms的条件下应用双线性变换对H∞控制器进行离散化，得到的离散控制器K（z）为

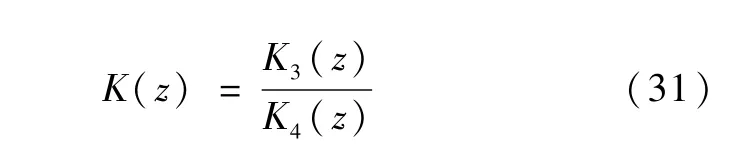
式中，

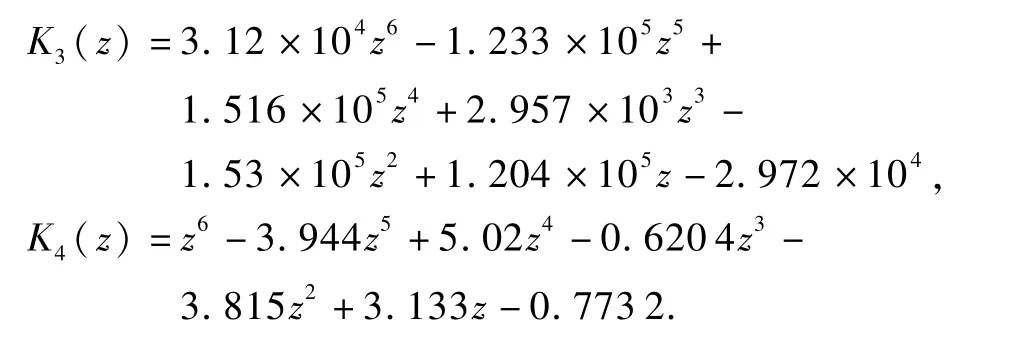
下面分析闭环系统的鲁棒稳定性.

系统被控对象模型存在摄动时的开环传递函数的频域特性如图6所示.

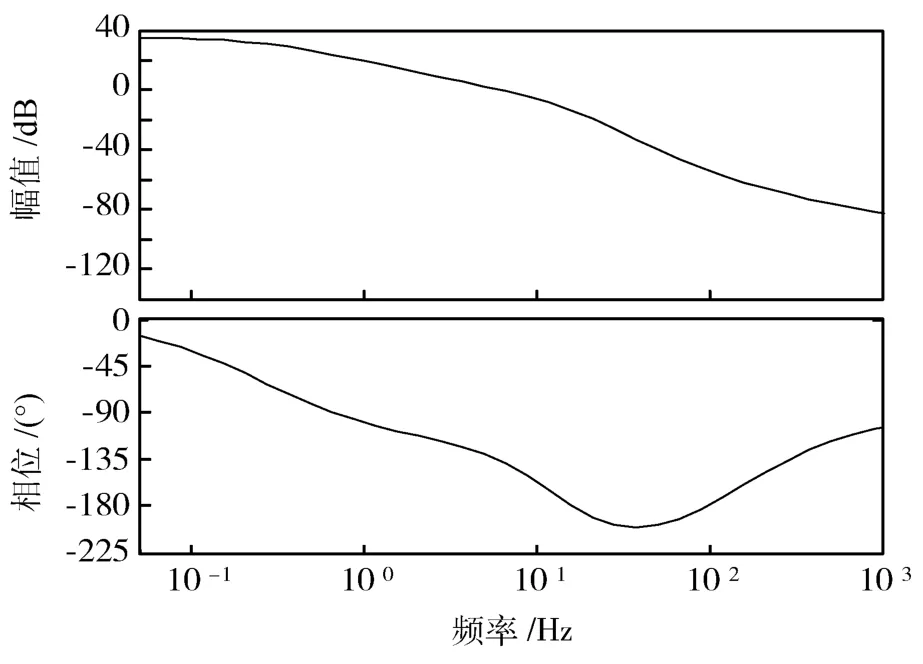
图6 系统对象摄动时的开环频率特性

由图6可知，被控对象模型存在摄动时系统的穿越频率为6 Hz，相角裕度为＋45°，满足稳定性条件.

不确定性摄动界函数1／Wy（s）与补灵敏度函数T（s）的幅频特性如图7所示.

图7 系统鲁棒性的摄动界

考虑到图7中不确定性摄动界函数1／Wy（s）表示系统鲁棒稳定性的界，而补灵敏度函数T（s）的幅频特性一直处于1／Wy（s）的幅频特性之下，即

则

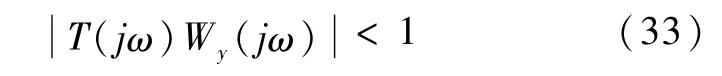
由小增益定理知，系统具有鲁棒稳定性.

3.4 系统测试结果

将离散化的H∞控制器K（z）应用于平移系统，分别输入正弦指令、斜坡指令，得到系统实际运行曲线如图8～10所示.

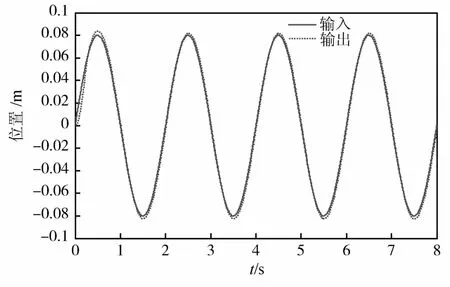
图8 正弦响应

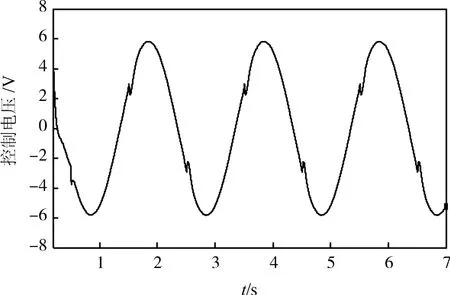
图9 正弦指令时的控制电压

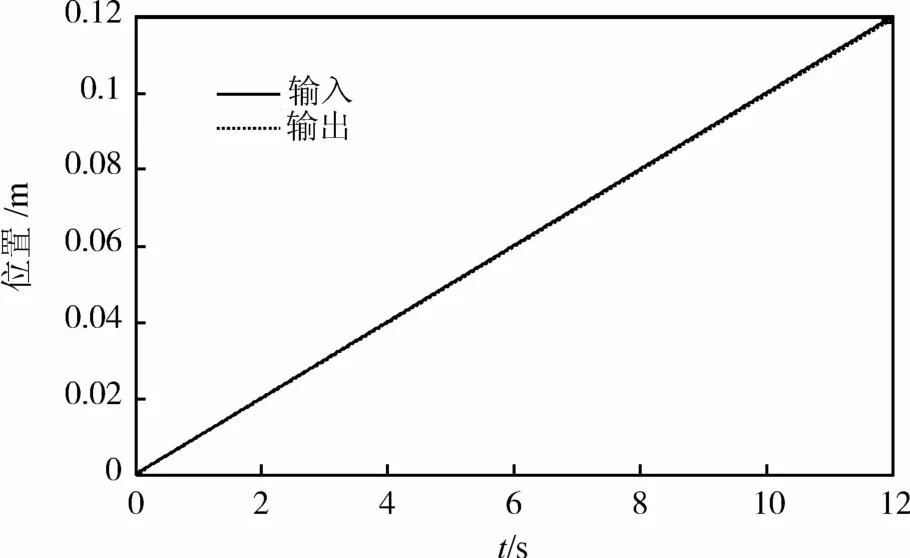
图10 斜坡响应

4 结 论

本文以九自由度空间交会对接模拟器横向平移控制系统设计为背景，采用了非结构不确定性描述系统中的高频谐振，并给出了对象的不确定性模型，确定了鲁棒H∞控制方案.研究了混合灵敏度问题的加权函数选取原则，并结合系统性能指标和主要不确定性给出了确定方法.推导了基于LMI的H∞控制律的存在条件，并给出了控制系统设计过程.系统测试结果满足指标要求，并经受住了用户长时间测试和仿真实验应用的考验，说明了本文方法可以解决实际系统的鲁棒性问题.

［1］ 杨嘉墀.航天器轨道动力学与控制（下）［M］.北京：宇航出版社，2007

［2］ Zhou K M，Doyle J C，Glover K.鲁棒与最优控制［M］.毛剑琴，钟宜生，林岩，译.北京：国防工业出版社，2006

［3］ 梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003

［4］ 赵希梅.永磁直线交流伺服系统的鲁棒跟踪控制研究［D］.沈阳工业大学硕士学位论文，2006

［5］ Zames G，Francis B A.Feedback minimax sensitivity and optimal robustness［J］.IEEE Trans Actions Automatic Control，1983，28（5）：585-601

［6］ Muhammad EM，Naeem As，Waqars.Weight selection in H∞loop shaping using lead／lag compensators［C］.IEEE 2ndInternational Conference on Emerging Technologies，Washington DC，USA，Nov 2006

［7］ 吴旭东，解学书.H∞鲁棒控制中的加权阵的选择［J］.清华大学学报（自然科学版），1997，1（37）：27-30

［8］ Iwasaki T，Skelton E.All controllers for the general H∞control problem：LM I existence conditions and state space formulas［J］.Automatica，1994，30（8）：1307-1317

［9］ Englewood C，Gahinet P.Explicit controller formulas for LM I-based H∞synthesis［J］.Automatica，1996，32（7）：1007-1014

Design of Space Rendezvous and Docking Transverse Linear Movement Simulator Control System Based on H∞Theory

LIGuiming1，2，YAO Yu3
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Key Laboratory of Science and Technology on Space Intelligent Control，Beijing 100190，China；3.Control and Simulation Center，Harbin Institute of Technology，Harbin 150001，China）

The paper investigates the design of simulator transverse linear movement control system for space rendezvous and docking，and discusses the unstructured uncertainty model.The robust H∞control strategy is designed according to performance indexes and main uncertainties，and the principle and method for choosing weighting functions of the mixed sensitivity optimal design are studied.The robust H∞controller is provided and obtained through solving three LMIs.The physical test resultsmeet the requestments，and show the effectiveness of the proposed method.

space rendezvous and docking simulator；transverse linearmovement control；H∞control

2009-02-01

李贵明（1983—），男，黑龙江人，博士研究生，研究方向为航天器导航、制导与控制（e-mail：hitlgm＠163.com）.

TP273

A

1674-1579（2009）06-0030-06